HĐ10 trang 38 Toán 12 Tập 2 - Kết nối tri thức

Giải Toán 12 Bài 14: Phương trình mặt phẳng - Kết nối tri thức

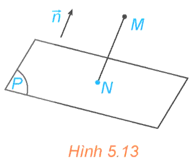
HĐ10 trang 38 Toán 12 Tập 2: Trong không gian Oxyz, cho điểm M(x0; y0; z0) và mặt phẳng (P): Ax + By + Cz + D = 0 có vectơ pháp tuyến $\overrightarrow{n}=\left(A;B;C\right)$. Gọi N là hình chiếu vuông góc của M trên (P) (H.5.13).

a) Giải thích vì sao tồn tại số k để $\overrightarrow{MN}=k\overrightarrow{n}$. Tính tọa độ của N theo k, tọa độ của M và các hệ số A, B, C, D.

b) Thay tọa độ của N vào phương trình mặt phẳng (P) để từ đó tính k theo tọa độ của M và các hệ số A, B, C, D.

c) Từ $\left|\overrightarrow{MN}\right|=\left|k\right|\left|\overrightarrow{n}\right|$, hãy tính độ dài của đoạn thẳng MN theo tọa độ của M và các hệ số A, B, C, D. Từ đó suy ra công thức tính khoảng cách từ điểm M đến mặt phẳng (P).

Lời giải:

a) Vì N là hình chiếu vuông góc của M trên (P) nên $MN\perp \left(P\right)$

Do đó $\overrightarrow{MN}$ sẽ cùng phương với vectơ pháp tuyến $\overrightarrow{n}$

Vậy tồn tại một số k sao cho $\overrightarrow{MN}=k\overrightarrow{n}$

Giả sử N(x₁; y₁; z₁). Suy ra $\overrightarrow{MN}=\left(x_1-x_0;y_1-y_0;z_1-z_0\right)$

Vì $\overrightarrow{MN}=k\overrightarrow{n}$ nên $\left\{\begin{array}{l}{x}_1-x_0=kA\\ y_1-y_0=kB\\ z_1-z_0=kC\end{array}\right.$$\iff \left\{\begin{array}{l}{x}_1=x_0+kA\\ y_1=y_0+kB\\ z_1=z_0+kC\end{array}\right.$

b) Thay tọa độ điểm N vào (P), ta được

A(x₀ + kA) + B(y₀ + kB) + C(z₀ + kC) + D = 0

⇔ k(A² + B² + C²) + Ax₀ + By₀ + Cz₀ + D = 0

$\iff k=\frac{-A{x}_0-B{y}_0-C{z}_0-D}{A^2+B^2+C^2}$

c) Ta có $\left|\overrightarrow{MN}\right|=\left|k\right|\left|\overrightarrow{n}\right|$$\iff \left|\overrightarrow{MN}\right|=\left|k\right|\sqrt{A^2+B^2+C^2}$

Mà $k=\frac{-A{x}_0-B{y}_0-C{z}_0-D}{A^2+B^2+C^2}$ nên $MN=\left|\frac{-A{x}_0-B{y}_0-C{z}_0-D}{A^2+B^2+C^2}\right|\sqrt{A^2+B^2+C^2}$

$\iff MN=\frac{\left|A{x}_0+B{y}_0+C{z}_0+D\right|}{\sqrt{A^2+B^2+C^2}}$

Do đó khoảng cách từ điểm M đến mặt phẳng (P) là $d=\frac{\left|A{x}_0+B{y}_0+C{z}_0+D\right|}{\sqrt{A^2+B^2+C^2}}$

Lời giải bài tập Toán 12 Bài 14: Phương trình mặt phẳng hay, chi tiết khác: