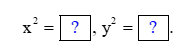Khám phá 1 trang 37 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 1: Căn bậc hai - Chân trời sáng tạo

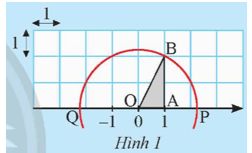
Khám phá 1 trang 37 Toán 9 Tập 1: Cho trục số được vẽ trên lưới ô vuông đơn vị như Hình 1.

a) Tính độ dài cạnh huyền OB của tam giác vuông OAB.

b) Vẽ đường tròn tâm O bán kính OB, đường tròn này cắt trục số tại hai điểm P và Q.

Gọi x là số thực được biểu diễn bởi P, y là số thực được biểu diễn bởi Q.

Thay mỗi  bằng số thích hợp để có các đẳng thức:

Lời giải:

a) Dựa vào lưới ô vuông trong Hình 1, ta có: OA = 1, AB = 2.

Áp dụng định lí Pythagore vào tam giác vuông OAB, ta có:

OB² = OA² + AB² = 1² + 2² = 5.

Suy ra $OB = \sqrt{5}$

Vậy độ dài cạnh huyền OB của tam giác vuông OAB là $\sqrt{5}$ .

b) Đường tròn tâm O bán kính OB cắt trục số tại hai điểm P và Q nên OP và OQ cũng là bán kính của đường tròn tâm O nên OB = OP = OQ = $\sqrt{5}$

Khi đó OB = OP = OQ = $\sqrt{5}$

Mà x là số thực được biểu diễn bởi P, y là số thực được biểu diễn bởi Q nên x = $\sqrt{5}$, y = $\sqrt{5}$

Do đó $x^2 = {\left(\sqrt{5}\right)}^2= 5, y^2 = {\left(\sqrt{5}\right)}^2 = 5$

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai hay, chi tiết khác: