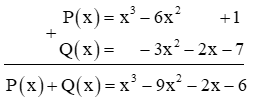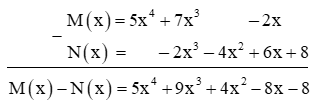Phép cộng, phép trừ đa thức một biến (Lý thuyết Toán lớp 7) - Cánh diều
Với tóm tắt lý thuyết Toán 7 Bài 3: Phép cộng, phép trừ đa thức một biến hay nhất, chi tiết sách Cánh diều
sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.
Phép cộng, phép trừ đa thức một biến (Lý thuyết Toán lớp 7) - Cánh diều
Lý thuyết Phép cộng, phép trừ đa thức một biến
1. Phép cộng đa thức một biến
– Để cộng hai đa thức một biến (theo cột dọc), ta có thể làm như sau:
+ Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
+ Đặt hai đơn thức có cùng số mũ của biến ở cùng cột;
+ Cộng hai đơn thức trong từng cột, ta có tổng cần tìm.
– Chú ý: Khi cộng đa thức theo cột dọc, nếu một đa thức khuyết số mũ nào của biến thì khi viết đa thức đó, ta bỏ trống cột tương ứng với số mũ trên.
Ví dụ: Cho hai đa thức: P(x) = x3 – 6x2 + 1 và Q(x) = –3x2 – 2x – 7. Tính tổng P(x) + Q(x) theo cột dọc.
Hướng dẫn giải
Ta thực hiện đặt phép tính cộng hai đa thức như sau:
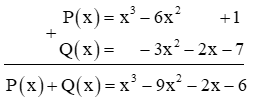
Vậy P(x) + Q(x) = x3 – 9x2 – 2x – 6.
– Để cộng hai đa thức một biến (theo hàng ngang), ta có thể làm như sau:
+ Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
+ Viết tổng hai đã thức theo hàng ngang;
+ Nhóm các đơn thức có cùng số mũ của biến với nhau;
+ Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm.
Ví dụ: Cho hai đa thức: P(x) = x3 – 6x2 + 1 và Q(x) = –3x2 – 2x – 7. Tính tổng P(x) + Q(x) theo hàng ngang.
Hướng dẫn giải
Ta có:
P(x) + Q(x) = (x3 – 6x2 + 1) + (–3x2 – 2x – 7)
= x3 – 6x2 + 1 – 3x2 – 2x – 7
= x3 + (– 6x2 – 3x2) – 2x + (1 – 7)
= x3 – 9x2 – 2x – 6.
Vậy P(x) + Q(x) = x3 – 9x2 – 2x – 6.
2. Trừ hai đa thức một biến
– Để trừ đa thức P(x) cho đa thức Q(x) (theo cột dọc), ta có thể làm như sau:
+ Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
+ Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức của P(x) ở trên và đơn thức của Q(x) ở dưới;
+ Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.
Ví dụ: Cho M(x) = 5x4 + 7x3 – 2x và N(x) = –2x3 – 4x2 + 6x + 8. Tính hiệu M(x) – N(x) theo cột dọc.
Hướng dẫn giải
Ta thực hiện đặt phép tính trừ hai đa thức như sau:
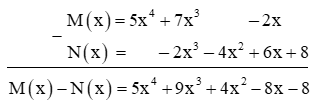
Vậy M(x) – N(x) = 5x4 + 9x3 + 4x2 – 8x – 8.
– Để trừ đa thức P(x) cho đa thức Q(x) (theo hàng ngang), ta có thể làm như sau:
+ Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
+ Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc;
+ Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau;
+ Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
Ví dụ: Cho M(x) = 5x4 + 7x3 – 2x và N(x) = –2x3 – 4x2 + 6x + 8. Tính hiệu M(x) – N(x) theo hàng ngang.
Hướng dẫn giải
Ta có:
M(x) – N(x) = (5x4 + 7x3 – 2x) – (–2x3 – 4x2 + 6x + 8)
= 5x4 + 7x3 – 2x + 2x3 + 4x2 – 6x – 8
= 5x4 + (7x2 + 2x3) + 4x2 + (–2x – 6x) – 8
= 5x4 + 9x3 + 4x2 – 8x – 8
Vậy M(x) – N(x) = 5x4 + 9x3 + 4x2 – 8x – 8.
Ví dụ: Xác định bậc của hai đa thức là tổng, hiệu của:
A(x) = –4x4 – 3x2 + 7 và B(x) = 4x4 – 5x2 + 8x – 1.
Hướng dẫn giải
Ta có:
• A(x) + B(x) = (–4x4 – 3x2 + 7) + (4x4 – 5x2 + 8x – 1)
= –4x4 – 3x2 + 7 + 4x4 – 5x2 + 8x – 1
= (–4x4 + 4x4) + (–3x2 – 5x2) + 8x + (7 – 1)
= –8x2 + 8x + 6
Do đó A(x) + B(x) = – 8x2 + 8x + 6.
Vậy bậc của A(x) + B(x) là 2.
• A(x) – B(x) = (–4x4 – 3x2 + 7) – (4x4 – 5x2 + 8x – 1)
= –4x4 – 3x2 + 7 – 4x4 + 5x2 – 8x + 1
= (–4x4 – 4x4) + (–3x2 + 5x2) – 8x + (7 + 1)
= –8x4 + 2x2 – 8x + 8
A(x) + B(x) = –8x4 + 2x2 – 8x + 8.
Vậy bậc của A(x) – B(x) là 4.
Bài tập Phép cộng, phép trừ đa thức một biến
Bài 1. Cho đa thức P(x) = x4 – 5x3 + 4x – 5 và Q(x) = –x4 + 3x2 + 2x + 1.
a) Hãy tính tổng P(x) + Q(x) và tìm bậc của đa thức đó.
b) Tìm đa thức R(x) sao cho P(x) = R(x) + Q(x).
Hướng dẫn giải
a) Ta có: P(x) + Q(x) = (x4 – 5x3 + 4x – 5) + (–x4 + 3x2 + 2x + 1)
= x4 – 5x3 + 4x – 5 – x4 + 3x2 + 2x + 1
= (x4 – x4) – 5x3 + 3x2 + (4x + 2x) + (1 – 5)
= –5x3 + 3x2 + 6x – 4
Vậy P(x) + Q(x) = –5x3 + 3x2 + 6x – 4.
Bậc của đa thức P(x) + Q(x) là 3.
b) Ta có: P(x) = R(x) + Q(x)
Suy ra R(x) = P(x) – Q(x)
Do đó R(x) = (x4 – 5x3 + 4x – 5) – (–x4 + 3x2 + 2x + 1)
= x4 – 5x3 + 4x – 5 + x4 – 3x2 – 2x – 1
= (x4 + x4) – 5x3 – 3x2 + (4x – 2x) + (–1 – 5)
= 2x4 – 5x3 + 3x2 + 2x – 6
Vậy R(x) = 2x4 – 5x3 + 3x2 + 2x – 6.
Bài 2. Bạn Minh cho rằng: “Tổng của hai đa thức bậc ba luôn là đa thức bậc ba”.
Bạn Quân cho rằng: “Hiệu của hai đa thức bậc ba luôn là đa thức bậc ba”.
Bạn Nam cho rằng: “Tổng và hiệu của hai đa thức bậc ba chưa chắc là đa thức bậc ba”.
Theo em, bạn nào đã nói đúng?
Hướng dẫn giải
• Ta lấy ví dụ:
Cho hai đa thức bậc ba A(x) = –x3 + 2x + 1 và B(x) = x3 + 3
Ta thấy:
A(x) + B(x)
= –x3 + 2x + 1 + x3 + 3
= (–x3 + x3) + 2x + (1 + 3)
= 2x + 4
Đa thức này không phải là đa thức bậc ba nên Minh nói không đúng.
Từ đó ta thấy tổng của hai đa thức bậc ba chưa chắc là đa thức bậc ba nên Nam nói đúng.
• Ta có ví dụ: P(x) = –2x3 + x2 + 5x và Q(x) = –2x3 + 4x2 + 2x + 3
Ta thấy:
P(x) – Q(x)
= –2x3 + x2 + 5x – (–2x3 + 4x2 + 2x + 3)
= –2x3 + x2 + 5x + 2x3 – 4x2 – 2x – 3
= (–2x3 + 2x3) + (x2 – 4x2) + (5x – 2x) – 3
= –3x2 + 3x – 3
Đa thức này không phải là đa thức bậc ba nên Quân nói chưa đúng.
Từ đó ta thấy hiệu của hai đa thức bậc ba chưa chắc là đa thức bậc ba nên Nam nói đúng.
Vậy Nam nói đúng.
Bài 3. Bác Hoa gửi ngân hàng thứ nhất 100 triệu đồng với kì hạn 1 năm, lãi suất x%/năm. Bác Hoa gửi ngân hàng thứ hai 100 triệu đồng với kì hạn 1 năm, lãi suất (x + 1,5)%/năm. Hết kì hạn 1 năm, bác Hoa có được cả gốc lẫn lãi là bao nhiêu ở cả hai ngân hàng?
Hướng dẫn giải
Số tiền lãi ở ngân hàng thứ nhất sau 1 năm là:
(triệu đồng)
Số tiền cả gốc lẫn lãi ở ngân hàng thứ nhất sau kì hạn 1 năm là:
100 + x (triệu đồng)
Số tiền lãi ở ngân hàng thứ hai là:
(triệu đồng)
Số tiền cả gốc lẫn lãi ở ngân hàng thứ hai sau kì hạn 1 năm là:
100 + x + 1,5 = 101,5 + x (triệu đồng)
Số tiền bác An có được khi hết kì hạn 1 năm ở cả hai ngân hàng là:
100 + x + 101,5 + x = 2x + 201,5 (triệu đồng)
Vậy sau 1 năm bác Hoa nhận được 2x + 201,5 triệu đồng cả gốc lẫn lãi.
Học tốt Phép cộng, phép trừ đa thức một biến
Các bài học để học tốt Phép cộng, phép trừ đa thức một biến Toán lớp 7 hay khác:


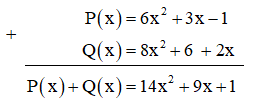
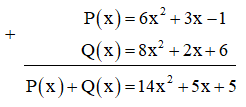
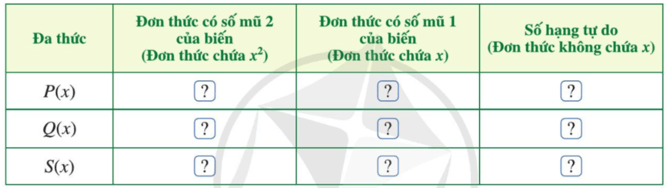
 ở bảng sau rồi trừ hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
ở bảng sau rồi trừ hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột: