Với giải bài tập Toán 7 Bài tập cuối chương 4 trang 87 sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán 7 trang 87.

Giải Toán 7 Kết nối tri thức Bài tập cuối chương 4 trang 87

Video Giải Toán 7 Bài tập cuối chương 4 - Cô Trần Thị Ngọc Anh (Giáo viên VietJack)

Bài tập (trang 87)

Giải Toán 7 trang 87 Tập 1

Bài 4.33 trang 87 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài tập cuối chương 4

Bài 4.33 trang 87 Toán 7 Tập 1: Tính các số đo x, y trong các tam giác dưới đây (H.4.75).

Lời giải:

Xét hình đầu tiên:

Ta có $x+x+20°+x+10°=180°.$

hay $3\text{x}+30°=180°$ hay $3\text{x}=180°-30°=150°.$

 Do đó $x=50°.$

Xét hình thứ hai:

Ta có $60°+y+2y=180°.$

hay $60°+3y=180°$ hay $3y=180°-60°=120°.$

Do đó $y=40°.$

Vậy $x=50°,y=40°.$

Lời giải bài tập Toán 7 Bài tập cuối chương 4 hay khác:

Bài 4.34 trang 87 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài tập cuối chương 4

Bài 4.34 trang 87 Toán 7 Tập 1: Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng $\widehat{MAN}=\widehat{MBN}.$

Lời giải:

Xét hai tam giác MAN và MBN có:

AM = BM (theo giả thiết).

MN chung.

AN = BN (theo giả thiết).

Do đó $\Delta MAN=\Delta MBN$ (c – c – c).

Vậy $\widehat{MAN}=\widehat{MBN}$ (2 góc tương ứng).

Lời giải bài tập Toán 7 Bài tập cuối chương 4 hay khác:

Bài 4.35 trang 87 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài tập cuối chương 4

Bài 4.35 trang 87 Toán 7 Tập 1: Trong Hình 4.77, có AO = BO, $\widehat{OAM}=\widehat{OBN}.$ Chứng minh rằng AM = BN.

Lời giải:

Xét hai tam giác OAM và OBN có:

$\widehat{OAM}=\widehat{OBN}$ (theo giả thiết).

AO = BO (theo giả thiết).

$\widehat{O}$ chung.

Do đó $\Delta OAM=\Delta OBN$ (g – c – g).

Vậy AM = BN (2 cạnh tương ứng).

Lời giải bài tập Toán 7 Bài tập cuối chương 4 hay khác:

Bài 4.36 trang 87 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài tập cuối chương 4

Bài 4.36 trang 87 Toán 7 Tập 1: Trong Hình 4.78, ta có AN = BM, $\widehat{BAN}=\widehat{ABM}.$ Chứng minh rằng  $\widehat{BAM}=\widehat{ABN}.$

Lời giải:

Xét hai tam giác BAM và ABN có:

AB chung.

$\widehat{ABM}=\widehat{BAN}$ (theo giả thiết).

BM = AN (theo giả thiết).

Do đó $\Delta BAM=\Delta ABN$ (c – g – c).

Vậy $\widehat{BAM}=\widehat{ABN}$ (2 góc tương ứng).

Lời giải bài tập Toán 7 Bài tập cuối chương 4 hay khác:

Bài 4.37 trang 87 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài tập cuối chương 4

Bài 4.37 trang 87 Toán 7 Tập 1: Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Chứng minh rằng MB = NB và góc AMB bằng góc ANB.

Lời giải:

Do M nằm trên đường trung trực của đoạn thẳng AB nên MA = MB.

Do N nằm trên đường trung trực của đoạn thẳng AB nên NA = NB.

Mà MA = NA (theo giải thiết có AM = AN) nên MA = MB = NA = NB.

Suy ra MB = NB.

Xét tam giác AMB và tam giác ANB có:

MA = NA (giả thiết)

MB = NB (chứng minh trên)

AB: cạnh chung

Do đó, ∆AMB = ∆ANB (c – c – c).

Suy ra $\widehat{AMB}=\widehat{ANB}$ (hai góc tương ứng).

Vậy MB = NB và $\widehat{AMB}=\widehat{ANB}$.

Lời giải bài tập Toán 7 Bài tập cuối chương 4 hay khác:

Bài 4.38 trang 87 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài tập cuối chương 4

Bài 4.38 trang 87 Toán 7 Tập 1: Cho tam giác ABC cân tại A có $\widehat{A}=120°.$ Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC.

Chứng minh rằng:

a) $\Delta BAM=\Delta CAN;$

b) Các tam giác ANB, AMC lần lượt cân tại N, M.

Lời giải:

a) Do $MA\perp AB,NA\perp AC$ nên tam giác BAM vuông tại A, tam giác CAN vuông tại A.

Do tam giác ABC cân tại A nên AB = AC, $\widehat{ABC}=\widehat{ACB}$ hay $\widehat{ABM}=\widehat{ACN}.$

Xét hai tam giác BAM vuông tại A và CAN vuông tại A có:

$\widehat{ABM}=\widehat{ACN}$ (chứng minh trên).

AB = AC (chứng minh trên).

Vậy $\Delta BAM=\Delta CAN$ (góc nhọn – cạnh góc vuông).

b) Xét tam giác ABC có: $\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180°.$

Mà $\widehat{ABC}=\widehat{ACB}$ (do tam giác ABC cân tại A).

Do đó $2\widehat{ABC}=180°-\widehat{BAC}=180°-120°=60°.$

Do đó $\widehat{ABC}=\widehat{ACB}=30°.$

Do $\Delta BAM=\Delta CAN$ (chứng minh ở ý a) nên AM = AN (2 cạnh tương ứng).

Do đó tam giác AMN cân tại A (1).

Xét tam giác CAN vuông tại A có $\widehat{ANC}+\widehat{ACN}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau).

Do đó $\widehat{ANC}=90°-\widehat{ACN}=90°-30°=60°.$

Từ (1) và (2) suy ra tam giác AMN đều.

Do đó $\widehat{MAN}=60°.$

Ta có: $\widehat{MAN}+\widehat{NAB}=\widehat{MAB}$

Suy ra $\widehat{NAB}=\widehat{MAB}-\widehat{MAN}=90°-60°=30°.$

Do đó $\widehat{NAB}=\widehat{ABN}=30°.$

Suy ra tam giác ANB cân tại N.

Ta có: $\widehat{MAN}+\widehat{MAC}=\widehat{NAC}$

Suy ra $\widehat{MAC}=\widehat{NAC}-\widehat{MAN}=90°-60°=30°.$

Do đó $\widehat{MAC}=\widehat{MCA}=30°.$

Suy ra tam giác AMC cân tại M.

Lời giải bài tập Toán 7 Bài tập cuối chương 4 hay khác:

Bài 4.39 trang 87 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài tập cuối chương 4

Bài 4.39 trang 87 Toán 7 Tập 1: Cho tam giác ABC vuông tại A có $\widehat{B}=60°.$ Trên cạnh BC lấy điểm M sao cho $\widehat{CAM}=30°.$ Chứng minh rằng:

a) Tam giác CAM cân tại M;

b) Tam giác BAM là tam giác đều;

c) M là trung điểm của đoạn thẳng BC.

Lời giải:

a) Xét tam giác ABC vuông tại A có $\widehat{ABC}+\widehat{ACB}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau).

Do đó $\widehat{ACB}=90°-\widehat{ABC}=90°-60°=30°.$

$\widehat{ACM}=\widehat{ACB}$ nên $\widehat{ACM}=30°.$

Tam giác CAM có $\widehat{ACM}=\widehat{CAM}=30°$ nên tam giác CAM cân tại M.

Vậy tam giác CAM cân tại M.

b) Có $\widehat{BAC}=\widehat{BAM}+\widehat{MAC}.$

 Do đó $\widehat{BAM}=\widehat{BAC}-\widehat{MAC}=90°-30°=60°.$

$\widehat{ABM}=\widehat{ABC}$ nên $\widehat{ABM}=60°.$

Xét tam giác BAM có $\widehat{ABM}+\widehat{BAM}+\widehat{BMA}=180°.$

Do đó

$$\begin{gathered} \widehat{BMA}=180°-\widehat{ABM}-\widehat{BAM} \\ =180°-60°-60°=60°. \end{gathered}$$

Tam giác BAM có $\widehat{ABM}=\widehat{BAM}=\widehat{BMA}=60°$ nên tam giác BAM là tam giác đều.

Vậy tam giác BAM là tam giác đều.

c) Do tam giác CAM cân tại M nên MA = MC (1).

Do tam giác BAM là tam giác đều nên MA = MB (2).

Từ (1) và (2) ta có MB = MC.

Mà M nằm giữa B và C nên M là trung điểm của BC.

Vậy M là trung điểm của BC.

Lời giải bài tập Toán 7 Bài tập cuối chương 4 hay khác:

Sách bài tập Toán 7 Ôn tập chương 4 trang 71, 72, 73, 74 - Kết nối tri thức

Với giải sách bài tập Toán 7 Ôn tập chương 4 trang 71, 72, 73, 74 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Ôn tập chương 4.

Giải sách bài tập Toán 7 Ôn tập chương 4 trang 71, 72, 73, 74 - Kết nối tri thức

A. Câu hỏi (trắc nghiệm)

Tìm câu trả lời đúng trong các đáp án đã cho.

Giải SBT Toán 7 trang 71 Tập 1

Vở thực hành Toán 7 Bài tập cuối chương 4 trang 78, 79, 80, 81 - Kết nối tri thức

Với giải vở thực hành Toán lớp 7 Bài tập cuối chương 4 trang 78, 79, 80, 81 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài tập cuối chương.

Giải Vở thực hành Toán 7 Bài tập cuối chương 4 trang 78, 79, 80, 81 - Kết nối tri thức

Giải VTH Toán 7 trang 78 Tập 1

Tổng hợp lý thuyết Toán 7 Chương 4 Kết nối tri thức

Với Tổng hợp lý thuyết Toán 7 Chương 4: Tam giác bằng nhau sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tổng hợp lý thuyết Toán 7 Chương 4 Kết nối tri thức

Lý thuyết tổng hợp Toán 7 Chương 4

1. Tổng các góc trong một tam giác

• Tổng ba góc trong một tam giác bằng 180°.

• Mỗi góc ngoài của một tam giác có số đo bằng tổng số đo hai góc trong không kề với nó.

• Phân loại tam giác dựa vào số đo góc:

+ Tam giác có ba góc đều nhọn được gọi là tam giác nhọn.

+ Tam giác có một góc tù được gọi là tam giác tù.

+ Tam giác có một góc vuông được gọi là tam giác vuông.

• Hai góc có tổng số đo bằng 90° được gọi là hai góc phụ nhau. Trong tam giác vuông hai góc nhọn phụ nhau.

2. Hai tam giác bằng nhau

• Hai tam giác bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

3. Các trường hợp bằng nhau của hai tam giác

• Trường hợp bằng nhau thứ nhất: cạnh - cạnh - cạnh (c.c.c)

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

• Trường hợp bằng nhau thứ hai: cạnh – góc – cạnh (c.g.c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

• Trường hợp bằng nhau thứ ba: góc – cạnh – góc (g.c.g)

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

4. Các trường hợp bằng nhau của hai tam giác vuông

• Trường hợp: hai cạnh góc vuông

Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Trường hợp: cạnh góc vuông – góc nhọn kề

Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Trường hợp: cạnh huyền – góc nhọn

Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

• Trường hợp: cạnh huyền – cạnh góc vuông

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

5. Tam giác cân

• Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.

• Tính chất:

+ Trong tam giác cân, hai góc ở đáy bằng nhau.

+ Tam giác có hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân.

• Tam giác đều là tam giác có ba cạnh bằng nhau. Khi đó ba góc cũng bằng nhau và bằng 60°.

+ Một tam giác có ba cạnh hoặc ba góc bằng nhau thì tam giác ấy là tam giác đều.

+ Tam giác cân có 1 góc bằng 60° thì tam giác ấy là tam giác đều.

6. Đường trung trực của một đoạn thẳng

• Định nghĩa: Đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

• Tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.

• Đường trung trực của đoạn thẳng cũng là trục đối xứng của đoạn thẳng đó.

• Đường trung trực của đoạn thẳng là tập hợp tất cả các điểm cách đều hai mút của đoạn thẳng đó.

Bài tập tổng hợp Toán 7 Chương 4

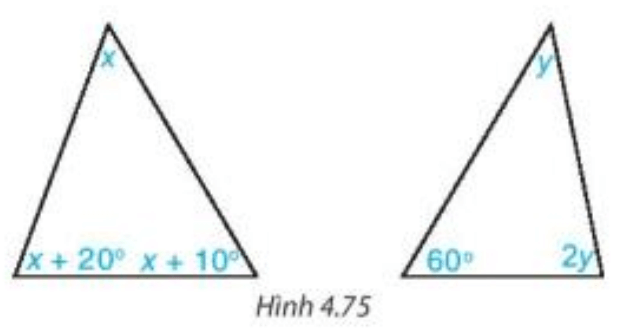
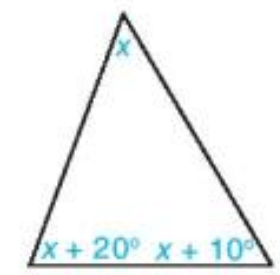
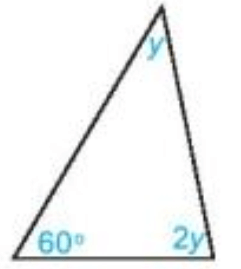
Bài 1. Tính số đo x, y trong các hình dưới đây:

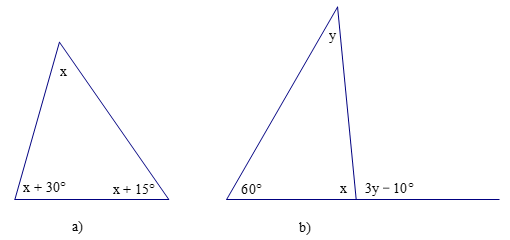
Hướng dẫn giải

a) Ta có: x + x + 30° + x + 15° = 180° (tổng ba góc trong tam giác)

⇒ 3x + 45° = 180°

⇒ 3x = 180° − 45°

⇒ 3x = 135°

⇒ x = 45°

Vậy x = 45°

b) Ta có: 3y – 10° = y + 60° (góc ngoài của tam giác)

⇒ 2y = 70°

⇒ y = 35°

Có: x + y + 60° = 180° (tổng ba góc trong tam giác)

⇒ x + 35° + 60° = 180°

⇒ x = 85°

Vậy x = 85°; y = 35°

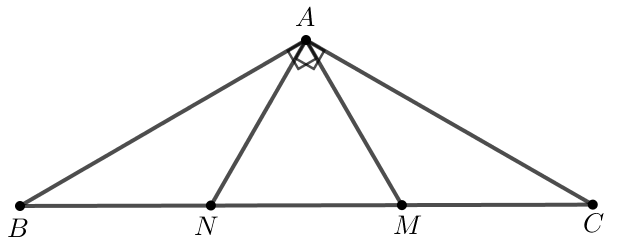
Bài 2. Cho hình dưới đây, biết tam giác ABC vuông tại A, BD là tia phân giác của góc ABC và BA = BE. Chứng minh rằng:

a) <$\Delta ABD=\Delta EBD$ và $\widehat{BED}=90°$>;

b) BD là đường trung trực của cạnh AE;

c) Tam giác BFC là tam giác cân.

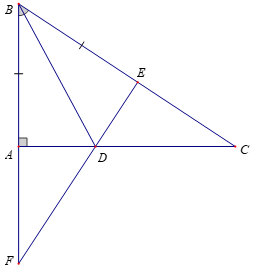
Hướng dẫn giải

a) Xét tam giác ABD và tam giác EBD có:

BA = BE (theo giả thiết)

$\widehat{ABD}=\widehat{EBD}$ (BD là tia phân giác của $\widehat{ABC}$)

BD là cạnh chung

Do đó, $\Delta ABD=\Delta EBD$ (c.g.c)

⇒ $\widehat{BAD}=\widehat{BED}$ (hai góc tương ứng)

Mà $\widehat{BAD}=90°$(theo giả thiết) ⇒ $\widehat{BED}=90°$ (đpcm)

b) Vì $\Delta ABD=\Delta EBD$ (chứng minh trên)

⇒ DA = DE (2 cạnh tương ứng)

⇒ D thuộc đường trung trực của AE (tính chất đường trung trực) (1)

Mà BA = BE (theo giả thiết)

⇒ B thuộc đường trung trực của AE (tính chất đường trung trực) (2)

Từ (1) và (2) ⇒ BD là đường trung trực của AE (đpcm)

c) Vì $\widehat{BED}=90°$ (chứng minh trên) ⇒ $\Delta EBF$ vuông tại E

Xét tam giác ABC (vuông tại A) và tam giác EBF (vuông tại E) có:

BA = BE (theo giả thiết)

$\widehat{ABC}$ là góc chung

⇒ $\Delta ABC=\Delta EBF$ (cạnh góc vuông – góc nhọn kề)

⇒ BC = BF (2 cạnh tương ứng)

⇒ $\Delta BFC$ cân tại B (đpcm).

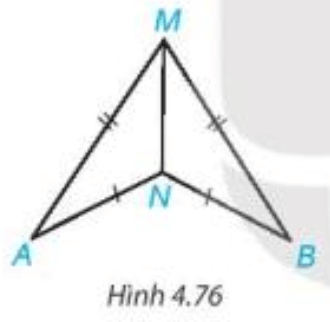
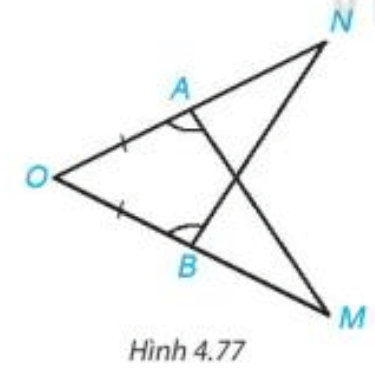
Bài 3. Cho M, N là hai điểm phân biệt nằm trên đường trung trực của cạnh AB sao cho AM = BN. O là giao điểm của MN và AB. Chứng minh rằng:

a) $\Delta AMO=\Delta BNO$;

b) Tam giác AMN cân;

c) Nếu $\widehat{AMO}=30°$ thì tam giác AMB là tam giác đều.

Hướng dẫn giải

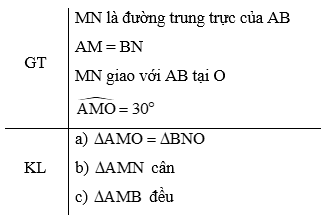
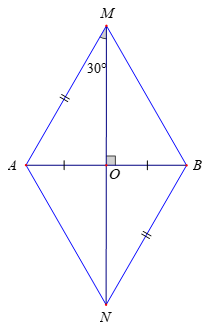
MN là đường trung trực của AB ⇒ MN ⊥ AB tại O và OA = OB

a) Xét hai tam giác vuông AMO và BNO có:

AM = BN (theo giả thiết)

OA = OB

⇒ $\Delta AMO=\Delta BNO$ (cạnh huyền – cạnh góc vuông)

b) Ta có: AN = BN (vì N thuộc đường trung trực của AB)

Mà AM = BN (theo giả thiết)

⇒ AN = AM

⇒ $\Delta AMN$ cân cân tại A (đpcm)

c) Tam giác AMO vuông tại O có:

$\widehat{AMO}+\widehat{MAO}=90°$ (hai góc phụ nhau)

⇒ $30°+\widehat{MAO}=90°$

⇒ $\widehat{MAO}=60°$ hay $\widehat{MAB}=60°$

Có: MA = MB (vì M thuộc đường trung trực của AB)

⇒ $\Delta AMB$ là tam giác cân

Mà $\widehat{MAB}=60°$

⇒ $\Delta AMB$ là tam giác đều (đpcm).

Học tốt Toán 7 Chương 4

Các bài học để học tốt Chương 4 Toán lớp 7 hay khác:

30 Bài tập tổng hợp Toán 7 Chương 4 Kết nối tri thức có lời giải

Với 30 bài tập trắc nghiệm tổng hợp Toán lớp 7 Chương 4: Tam giác bằng nhau có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

30 Bài tập tổng hợp Toán 7 Chương 4 Kết nối tri thức có lời giải

Xem thử

Chỉ từ 150k mua trọn bộ trắc nghiệm Toán 7 Kết nối tri thức (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: