Với giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán 7 Bài 3.

Giải Toán 7 Chân trời sáng tạo Bài 3: Đại lượng tỉ lệ nghịch

Hoạt động khởi động

Giải Toán 7 trang 16 Tập 2

Khởi động trang 16 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Khởi động trang 16 Toán 7 Tập 2: Một người đi xe đạp từ A đến B với vận tốc không đổi là 20 km/h mất 6 giờ. Hỏi nếu người đó đi bằng xe gắn máy với vận tốc không đổi là 40 km/h thì mất bao nhiêu thời gian?

Lời giải:

Gọi thời gian người đó đi với vận tốc 40 km/h là x giờ (x > 0).

Vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên $\frac{20}{40}=\frac{x}{6}$

hay $\frac{1}{2}=\frac{x}{6}$do đó 2x = 6 suy ra x = 3 (thỏa mãn).

Vậy nếu người đó đi với vận tốc 40 km/h thì mất 3 giờ.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Khám phá 1 trang 16 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Khám phá 1 trang 16 Toán 7 Tập 2:

a) Mẹ của Mai nhập về 20 kg đậu xanh để bán. Mai giúp mẹ chia đậu thành các gói nhỏ bằng nhau để dễ bán. Gọi s là số gói, m (kg) là khối lượng mỗi gói.

Em hãy tính tích s . m và tìm s khi:

m = 0,5;

m = 1;

m = 2;

b) Một vòi nước chảy vào bể cạn có dung tích 100 l. Gọi V là số lít nước chảy được từ vòi vào bể trong một giờ và gọi t là thời gian để vòi chảy đầy bể.

Em hãy lập công thức tính t theo V và tìm t khi:

V = 50;

V = 100;

V = 200.

Lời giải:

a) Do s là số gói, m là khối lượng đậu xanh mỗi gói nên s . m là tổng khối lượng đậu xanh.

Do đó s . m = 20.

Với m = 0,5 thì s = 20 : 0,5 = 40.

Với m = 1 thì s = 20 : 1 = 20.

Với m = 2 thì s = 20 : 2 = 10.

b) Do V là số lít nước chảy được từ vòi vào bể trong một giờ và t là thời gian để vòi chảy đầy bể với dung tích của bể là 100 l nên $\frac{100}{V}=t$.

Với V = 50 thì t = 100 : 50 = 2.

Với V = 100 thì t = 100 : 100 = 1.

Với V = 200 thì t = 100 : 200 = $\frac{100}{200}=\frac{1}{2}=0,5$.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Thực hành trang 17 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

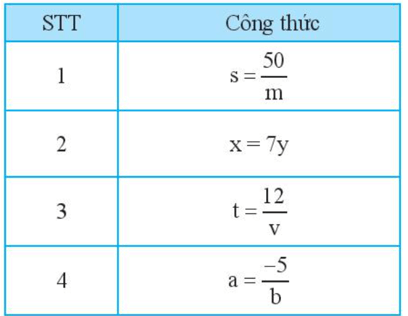
Thực hành trang 17 Toán 7 Tập 2: Tìm các đại lượng tỉ lệ nghịch trong mỗi công thức sau:

Lời giải:

Xét công thức (1) ta có $s=\frac{50}{m}$nên sm = 50.

Do đó s và m là hai đại lượng tỉ lệ nghịch với nhau.

Xét công thức (2) ta có x = 7y nên x và y là hai đại lượng tỉ lệ thuận với nhau.

Xét công thức (3) ta có $t=\frac{12}{v}$nên tv = 12.

Do đó t và v là hai đại lượng tỉ lệ nghịch với nhau.

Xét công thức (4) ta có $a=\frac{-5}{b}$nên ab = -5.

Do đó a và b là hai đại lượng tỉ lệ nghịch với nhau.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Vận dụng 1 trang 17 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Vận dụng 1 trang 17 Toán 7 Tập 2: Lan muốn cắt một hình chữ nhật có diện tích 12 cm². Gọi a (cm) và b (cm) là hai kích thước của hình chữ nhật đó. Em hãy viết công thức thể hiện mối quan hệ giữa hai đại lượng a và b.

Lời giải:

Do a và b là kích thước hai cạnh của hình chữ nhật có diện tích 12 cm² nên a.b = 12.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Khám phá 2 trang 17 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Khám phá 2 trang 17 Toán 7 Tập 2: Cho biết hai đại lượng y và x tỉ lệ nghịch với nhau:

a) Tìm hệ số tỉ lệ.

b) Tìm giá trị thích hợp cho mỗi dấu ? trong bảng trên.

c) Em có nhận xét gì về tích hai giá trị tương ứng x₁y₁; x₂y₂; x₃y₃; x₄y₄; x₅y₅ của x và y.

Lời giải:

a) Do y và x là hai đại lượng tỉ lệ nghịch với nhau và x₁y₁ = 1.10 = 10.

Vậy hệ số tỉ lệ bằng 10.

b) Do hệ số tỉ lệ của hai đại lượng tỉ lệ nghịch x và y bằng 10 nên:

Với x₂ = 2 thì y₂ = 10 : 2 = 5.

Với x₃ = 3 thì y₃ = 10 : 3 = $\frac{10}{3}$.

Với x₄ = 4 thì y₄ = 10 : 4 = $\frac{10}{4}$= 2,5.

Với x₅ = 5 thì y₅ = 10 : 5 = 2.

Ta có bảng sau:

c) Ta thấy x₁y₁ = x₂y₂ = x₃y₃ = x₄y₄ = x₅y₅ = 10.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Vận dụng 2 trang 18 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Vận dụng 2 trang 18 Toán 7 Tập 2: Bạn Quỳnh vừa học được phương pháp đọc sách mới, làm tăng gấp đôi số từ đọc được trong một phút so với phương pháp đọc sách cũ. Hãy cho biết tỉ số giữa thời gian đọc xong cùng một quyển sách theo phương pháp mới và cũ của bạn Quỳnh.

Lời giải:

Số từ đọc được trong một phút và thời gian đọc quyển sách là hai đại lượng tỉ lệ nghịch với nhau.

Khi đó do số từ đọc được trong một phút lúc sau bằng 2 lần số từ đọc được trong một phút lúc đầu nên thời gian đọc xong cùng một quyển sách theo phương pháp mới bằng $\frac{1}{2}$thời gian đọc xong quyển sách đó theo phương pháp cũ.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Vận dụng 3 trang 19 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Vận dụng 3 trang 19 Toán 7 Tập 2: Hãy giải bài toán ở Hoạt động khởi động trang 16.

Lời giải:

Gọi thời gian người đó đi với vận tốc 40 km/h là x giờ (x > 0).

Vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên $\frac{20}{40}=\frac{x}{6}$

hay $\frac{1}{2}=\frac{x}{6}$do đó 2x = 6 suy ra x = 3.

Vậy nếu người đó đi với vận tốc 40 km/h thì mất 3 giờ.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Bài 1 trang 20 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Bài 1 trang 20 Toán 7 Tập 2: Cho biết hai đại lượng a và b tỉ lệ nghịch với nhau và khi a = 3 thì b = -10.

a) Tìm hệ số tỉ lệ.

b) Hãy biểu diễn a theo b.

c) Tính giá trị của a khi b = 2, b = 14.

Lời giải:

a) Do a và b là hai đại lượng tỉ lệ nghịch với nhau và khi a = 3 thì b = -10 nên hệ số tỉ lệ bằng 3 . (-10) = -30.

b) Do ab = -30 nên a = $\frac{-30}{b}$.

c) Với b = 2 thì a = $\frac{-30}{2}$= -15.

Với b = 14 thì a = $\frac{-30}{14}=\frac{-15}{7}$.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Bài 2 trang 20 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Bài 2 trang 20 Toán 7 Tập 2: Cho hai đại lượng x và y tỉ lệ nghịch với nhau:

a) Tìm hệ số tỉ lệ.

b) Tìm các giá trị chưa biết trong bảng trên.

Lời giải:

a) Do x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = -8 thì y = -5 nên hệ số tỉ lệ bằng (-8) . (-5) = 40.

b) Với x = 5 thì y = 40 : 5 = 8.

Với x = 4 thì y = 40 : 4 = 10.

Với y = 9 thì x = 40 : 9 = $\frac{40}{9}$.

Với x = 6 thì y = 40 : 6 = $\frac{20}{3}$.

Với x = 12 thì y = 40 : 12 = $\frac{10}{3}$.

Ta có bảng sau:

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Bài 3 trang 20 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Bài 3 trang 20 Toán 7 Tập 2: Có 20 công nhân với năng suất làm việc như nhau đóng xong một chiếc tàu trong 60 ngày. Hỏi nếu chỉ còn 12 công nhân thì họ đóng xong chiếc tàu đó trong bao nhiêu ngày?

Lời giải:

Gọi thời gian 12 công nhân cần làm để đóng xong chiếc tàu là x ngày (x > 0).

Số công nhân và thời gian đóng tàu là hai đại lượng tỉ lệ nghịch nên $\frac{20}{12}=\frac{x}{60}$

Do đó 12x = 20 . 60 = 1 200.

Suy ra x = 1 200 : 12 = 100 (thỏa mãn).

Vậy 12 công nhân đóng tàu trong 100 ngày thì xong.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Bài 4 trang 20 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Bài 4 trang 20 Toán 7 Tập 2: Đội sản xuất Quyết Tiến dùng x máy gặt (có cùng năng suất) để gặt xong một cánh đồng hết y giờ. Hỏi đại lượng x và y có tỉ lệ nghịch với nhau không?

Lời giải:

Số mặt gặt và thời gian gặt là hai đại lượng tỉ lệ nghịch với nhau nên x và y là hai đại lượng tỉ lệ nghịch với nhau.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Bài 5 trang 20 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Bài 5 trang 20 Toán 7 Tập 2: Cho biết a (m) là chu vi của bánh xe, b là số vòng quay được của bánh xe trên đoạn đường xe đi từ A đến B. Hỏi a và b có phải là hai đại lượng tỉ lệ nghịch không?

Lời giải:

Trên một quãng đường, chu vi của bánh xe và số vòng quay của bánh xe là hai đại lượng tỉ lệ nghịch với nhau nên a và b là hai đại lượng tỉ lệ nghịch với nhau.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Bài 6 trang 20 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Bài 6 trang 20 Toán 7 Tập 2: Dựa theo bảng giá trị tương ứng của hai đại lượng trong mỗi trường hợp sau, hãy cho biết hai đại lượng có tỉ lệ nghịch với nhau hay không.

a)

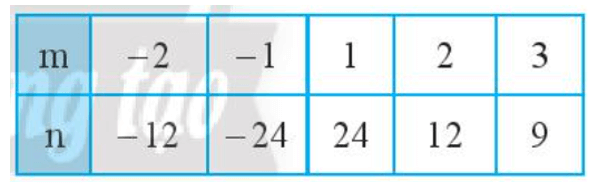
b)

Lời giải:

a) Ta thấy 1.60 = 2.30 = 3.20 = 4.15 = 5.12 = 60 nên a và b là hai đại lượng tỉ lệ nghịch với nhau.

b) Ta thấy (-2) . (-12) = (-1) . (-24) = 1.24 = 2.12 = 24; 3.9 = 27.

Do 24 ≠ 27 nên m và n không phải hai đại lượng tỉ lệ nghịch với nhau.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Bài 7 trang 20 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Bài 7 trang 20 Toán 7 Tập 2: Một nông trường có 2 máy gặt (có cùng năng suất) đã gặt xong một cánh đồng hết 4 giờ. Hỏi nếu có 4 máy gặt như thế sẽ gặt xong cánh đồng đó hết bao nhiêu thời gian?

Lời giải:

Gọi thời gian để 4 máy gặt gặt xong cánh đồng là x giờ (x > 0).

Số máy gặt và thời gian gặt là hai đại lượng tỉ lệ nghịch với nhau nên $\frac{2}{4}=\frac{x}{4}$.

Do đó x = 2.

Vậy 4 máy gặt gặt xong cánh đồng trong 2 giờ.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Bài 8 trang 20 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Bài 8 trang 20 Toán 7 Tập 2: Lan muốn cắt một hình chữ nhật có diện tích bằng 24 cm². Gọi n (cm) và d (cm) là độ dài hai cạnh của hình chữ nhật. Hãy chứng tỏ n là d tỉ lệ nghịch với nhau và tính n theo d.

Lời giải:

Do n và d là độ dài hai cạnh của hình chữ nhật có diện tích bằng 24 cm² nên nd = 24.

Do đó n và d là hai đại lượng tỉ lệ nghịch với nhau.

Khi đó n = $\frac{24}{d}$.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Bài 9 trang 20 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Bài 9 trang 20 Toán 7 Tập 2: Một đoàn tàu lửa chuyển động đều trên quãng đường 200 km với vận tốc v (km/h) trong thời gian t (h). Hãy chứng tỏ v, t tỉ lệ nghịch với nhau và tính t theo v.

Lời giải:

Quãng đường bằng vận tốc nhân thời gian nên 200 = vt.

Do đó v và t là hai đại lượng tỉ lệ nghịch với nhau.

Khi đó t = $\frac{200}{v}$.

Lời giải bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay, chi tiết khác:

Sách bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Với giải sách bài tập Toán 7 Bài 3: Đại lượng tỉ lệ nghịch sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 3.

Giải SBT Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Giải SBT Toán 7 trang 16 Tập 2

Vở thực hành Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

Với giải vở thực hành Toán lớp 7 Bài 3: Đại lượng tỉ lệ nghịch sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài 3.

Giải vở thực hành Toán 7 Bài 3: Đại lượng tỉ lệ nghịch - Chân trời sáng tạo

B. Câu hỏi trắc nghiệm

Chọn phương án đúng trong mỗi câu sau:

Giải VTH Toán 7 trang 9 Tập 2

Đại lượng tỉ lệ nghịch (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

Với tóm tắt lý thuyết Toán 7 Bài 3: Đại lượng tỉ lệ nghịch hay nhất, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Đại lượng tỉ lệ nghịch (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

Lý thuyết Đại lượng tỉ lệ nghịch

1. Khái niệm:

Cho a là một hằng số khác 0. Nếu đại lượng y liên hệ với đại lượng x theo công thức $y=\frac{a}{x}$ hay xy = a thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.

Ví dụ:

+ Nếu x.y = 2 thì ta nói x tỉ lệ nghịch với y theo hệ số tỉ lệ là 2.

+ $v=\frac{300}{t}$ nên ta nói v tỉ lệ nghịch với t theo hệ số tỉ lệ là 300.

Chú ý: Khi y tỉ lệ nghịch với x thì x cũng tỉ lệ nghịch với y và ta nói hai đại lượng đó tỉ lệ nghịch với nhau.

Ví dụ:Nếu x.y = 7 ta có x tỉ lệ nghịch với y với hệ số tỉ lệ là 7 và y cũng tỉ lệ nghịch với x với hệ số tỉ lệ là 7.

Khi đó, ta nói x và y tỉ lệ nghịch với nhau với hệ số tỉ lệ là 7.

2. Tính chất của các đại lượng tỉ lệ nghịch:

Nếu hai đại lượng y và x tỉ lệ nghịch với nhau thì:

- Tích hai giá trị tương ứng của chúng luôn không đổi (bằng hệ số tỉ lệ):

x₁y₁ = x₂y₂ = x₃y₃ = … hay $\frac{x_1}{\frac{1}{y_1}}=\frac{x_2}{\frac{1}{y_2}}=\frac{x_3}{\frac{1}{y_3}}=\mathrm{...}$

- Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia:

$\frac{x_1}{x_2}=\frac{x_2}{y_1}$; $\frac{x_1}{x_3}=\frac{y_3}{y_1}$ ; …

Ví dụ: Cho bảng sau. Trong đó x và y là hai đại lượng tỉ lệ nghịch với nhau.

Khi đó ta có:

+) x₁.y₁ = x₂.y₂ = x₃.y₃ = x₄.y₄ = 16.

+) $\frac{x_1}{x_2}=\frac{y_2}{y_1}=2$ ; $\frac{x_2}{x_3}=\frac{y_3}{y_2}=8$ ; …

Bài tập Đại lượng tỉ lệ nghịch

Bài 1. Cho biết hai đại lượng a và b tỉ lệ nghịch với nhau và khi a = −4 thì b = 5.

a) Tìm hệ số tỉ lệ;

b) Hãy biểu diễn a theo b;

c) Tính giá trị của a khi b = 10;

d) Tính giá trị của b khi a = −5.

Hướng dẫn giải:

a) Do a và b là hai đại lượng tỉ lệ nghịch nên: hệ số tỉ lệ là:

a.b = (−4).5 = −20.

Vậy hệ số tỉ lệ của hai đại lượng tỉ lệ nghịch a và b là −20.

b) Theo câu a ta có a.b = −20. Suy ra $a=\frac{-20}{b}$ .

Vậy biểu diễn của a theo b là: $a=\frac{-20}{b}$ .

c) Từ câu b, ta có: $a=\frac{-20}{b}$ .

Khi b = 10 thì $a=\frac{-20}{10}=-2$ .

Vậy a = 2 khi b = 10.

d) Theo câu a ta có: a.b = −20 suy ra $b=\frac{-20}{a}$ .

Khi a = −5 thì $b=\frac{-20}{a}=\frac{-20}{-5}=4$ .

Vậy khi a = −5 thì b = 4.

Bài 2.

a) Dựa vào bảng giá trị tương ứng của a và b trong mỗi trường hợp sau, hãy cho biết hai đại lượng có tỉ lệ nghịch với nhau hay không.

b) Cho x và y là hai đại lượng tỉ lệ nghịch với nhau:

Hướng dẫn giải:

a) Ta thấy: 5.6 = 6.5 = 3.10 = (−3).(−10) =30.

Nên suy ra hai đại lượng a và b tỉ lệ nghịch với nhau.

b) Do x và y là hai đại lượng tỉ lệ nghịch với nhau nên ta có hệ số tỉ lệ là:

x.y =7.4 = 28

Suy ra x.y = 28.

Khi đó:

Nếu y = −7 thì $x=\frac{28}{y}=\frac{28}{-7}=-4$ ;

Nếu x = 2 thì $y=\frac{28}{x}=\frac{28}{2}=14$ .

Vậy ta có bảng giá trị bảng giá trị của x và y là:

Bài 3. Bác Hoàng muốn lát một sân gạch hình chữ nhật có diện tích là 28 m². Gọi e (m), f (m) lần lượt là độ dài hai cạnh của hình chữ nhật này. Hãy chứng tỏ e và f là hai đại lượng tỉ lệ nghịch. Tính e khi f = 4 m.

Hướng dẫn giải:

Diện tích của sân gạch hình chữ nhật là: e.f = 28 (m²).

Ta thấy e.f = 28 luôn không đổi.

Vậy suy ra e và f là hai đại lượng tỉ lệ nghịch với nhau.

Suy ra khi f = 4 m thì $e=\frac{28}{f}=\frac{28}{4}=7$ (m)

Vậy khi hình chữ nhật có một cạnh f = 4 m thì cạnh còn lại của hình chữ nhật này là: e = 7 m.

Bài 4. Cho biết một đội công nhân (năng suất làm việc như nhau) dự kiến làm xong một công trình trong vòng 156 ngày. Hỏi nếu chuyển $\frac{1}{4}$ số công nhân sang công trình khác thì số công nhân còn lại sẽ làm xong công trình này trong bao nhiêu ngày?

Hướng dẫn giải:

Số công nhân còn lại khi chuyển đi $\frac{1}{4}$ số công nhân ban đầu là $\frac{3}{4}$ số công nhân ban đầu.

Gọi a₁, a₂ (công nhân) lần lượt là số lượng công nhân có trong đội trước và sau đi chuyển đi (a₁, a₂ $\in$ ℕ*).

Gọi b₁, b₂ (ngày) lần lượt là số ngày hoàn thành công trình tương ứng trong hai trường hợp trên (b₁, b₂ $\in$ ℕ*).

Do đó số công nhân và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch (vì số lượng công việc để hoàn thành công việc là không đổi) nên ta có:

a₁b₁ = a₂b₂ suy ra $\frac{a_1}{a_2}=\frac{b_2}{b_1}$ .

Mặt khác ta có $\frac{a_1}{a_2}=\frac{4}{3}$ và b₁ =156 nên ta có:

$\frac{4}{3}=\frac{b_2}{156}$ suy ra $b_2=\frac{156.4}{3}=208$ (thỏa mãn)

Vậy số công nhân còn lại sẽ hoàn thành công trình trong 208 ngày.

Học tốt Đại lượng tỉ lệ nghịch

Các bài học để học tốt Đại lượng tỉ lệ nghịch Toán lớp 7 hay khác:

15 Bài tập Đại lượng tỉ lệ nghịch (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Đại lượng tỉ lệ nghịch Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Đại lượng tỉ lệ nghịch (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 7

Xem thử

Chỉ từ 150k mua trọn bộ trắc nghiệm Toán 7 Chân trời sáng tạo (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: