Với giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán 7 Bài 3.

Giải Toán 7 Chân trời sáng tạo Bài 3: Phép cộng và phép trừ đa thức một biến

Hoạt động khởi động

Giải Toán 7 trang 33 Tập 2

Khởi động trang 33 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Khởi động trang 33 Toán 7 Tập 2: Có thể cộng và trừ hai đa thức một biến như cộng và trừ hai số thực không?

Lời giải:

Ta có thể cộng và trừ hai đa thức một biến như cộng và trừ hai số thực.

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Khám phá 1 trang 33 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

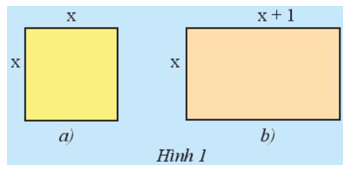
Khám phá 1 trang 33 Toán 7 Tập 2: Hãy lập biểu thức biểu thị tổng chu vi của hình vuông (Hình 1a) và hình chữ nhật (Hình 1b).

Lời giải:

Biểu thức biểu thị chu vi của hình vuông là: 4x.

Biểu thức biểu thị chu vi của hình chữ nhật là: 2 . (x + x + 1) = 2 . (2x + 1) = 2 . 2x + 2 . 1 = 4x + 2.

Biểu thức biểu thị tổng chu vi của hình vuông và hình chữ nhật là: 4x + 4x + 2 = 8x + 2.

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Thực hành 1 trang 34 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Thực hành 1 trang 34 Toán 7 Tập 2: Cho hai đa thức P(x) = 7x³ - 8x + 12 và Q(x) = 6x² - 2x³ + 3x - 5.

Hãy tính P(x) + Q(x) bằng hai cách.

Lời giải:

Cách 1:

P(x) + Q(x) = (7x³ - 8x + 12) + (6x² - 2x³ + 3x - 5)

P(x) + Q(x) = 7x³ - 8x + 12 + 6x² - 2x³ + 3x - 5

P(x) + Q(x) = (7x³ - 2x³) + 6x² + (-8x + 3x) + (12 - 5)

P(x) + Q(x) = 5x³ + 6x² - 5x + 7

Vậy P(x) + Q(x) = 5x³ + 6x² - 5x + 7.

Cách 2:

Q(x) = 6x² - 2x³ + 3x - 5 = -2x³ + 6x² + 3x - 5.

Khi đó thực hiện đặt phép tính ta có:

$\begin{array}{c}\underset{¯}{+\begin{array}{c}\begin{array}{c}-\end{array}\end{array}\begin{array}{c}\begin{array}{c}7{\text{x}}^3\\ 2{\text{x}}^3\end{array}\end{array}\begin{array}{c}\begin{array}{c}+\end{array}\end{array}\begin{array}{c}\begin{array}{c}6{\text{x}}^2\end{array}\end{array}\begin{array}{c}\begin{array}{c}-\\ +\end{array}\end{array}\begin{array}{c}\begin{array}{c}8\text{x}\\ 3\text{x}\end{array}\end{array}\begin{array}{c}\begin{array}{c}+\\ -\end{array}\end{array}\begin{array}{c}\begin{array}{c}12\\ 5\end{array}\end{array}}\\ 5{\text{x}}^3+6{\text{x}}^2-5\text{x}+7\end{array}$

Vậy P(x) + Q(x) = 5x³ + 6x² - 5x + 7.

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Khám phá 2 trang 34 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

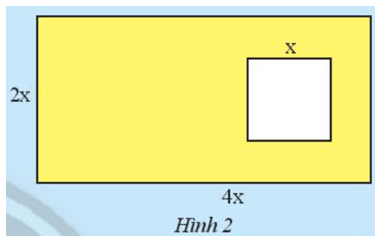
Khám phá 2 trang 34 Toán 7 Tập 2: Hình 2 gồm một hình chữ nhật có chiều dài 4x cm, chiều rộng 2x cm và hình vuông nhỏ bên trong có cạnh x cm.

Hãy lập biểu thức biểu thị diện tích của phần được tô màu vàng trong Hình 2.

Lời giải:

Biểu thức biểu thị diện tích của hình chữ nhật là: 4x . 2x = 8x².

Biểu thức biểu thị diện tích của hình vuông là: x².

Biểu thức biểu thị diện tích phần được tô vàng trong Hình 2 là: 8x² - x² = 7x².

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Thực hành 2 trang 35 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Thực hành 2 trang 35 Toán 7 Tập 2: Cho hai đa thức P(x) = 2x³ - 9x² + 5 và Q(x) = -2x² - 4x³ + 7x.

Hãy tính P(x) - Q(x) bằng hai cách.

Lời giải:

Cách 1:

P(x) - Q(x) = (2x³ - 9x² + 5) - (-2x² - 4x³ + 7x)

P(x) - Q(x) = 2x³ - 9x² + 5 + 2x² + 4x³ - 7x

P(x) - Q(x) = (2x³ + 4x³) + (-9x² + 2x²) - 7x + 5

P(x) - Q(x) = 6x³ - 7x² - 7x + 5

Vậy P(x) - Q(x) = 6x³ - 7x² - 7x + 5.

Cách 2:

Q(x) = -2x² - 4x³ + 7x = - 4x³ - 2x² + 7x

Khi đó thực hiện đặt phép tính ta có:

$\begin{array}{c}-\underset{¯}{\begin{array}{c}\begin{array}{c}-\end{array}\end{array}\begin{array}{c}\begin{array}{c}2{\text{x}}^3\\ 4{\text{x}}^3\end{array}\end{array}\begin{array}{c}\begin{array}{c}-\\ -\end{array}\end{array}\begin{array}{c}\begin{array}{c}9{\text{x}}^2\\ 2{\text{x}}^2\end{array}\end{array}\begin{array}{c}\begin{array}{c}+\end{array}\end{array}\begin{array}{c}\begin{array}{c}7\text{x}\end{array}\end{array}\begin{array}{c}\begin{array}{c}+\end{array}\end{array}\begin{array}{c}\begin{array}{c}5\end{array}\end{array}}\\ 6{\text{x}}^3-7{\text{x}}^2-7\text{x}+5\end{array}$

Vậy P(x) - Q(x) = 6x³ - 7x² - 7x + 5.

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Thực hành 3 trang 35 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Thực hành 3 trang 35 Toán 7 Tập 2: Thực hiện phép tính: (x - 4) + [(x² + 2x) + (7 - x)].

Lời giải:

(x - 4) + [(x² + 2x) + (7 - x)]

= x - 4 + x² + 2x + 7 - x

= x² + (x + 2x - x) + (-4 + 7)

= x² + 2x + 3

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 1 trang 35 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Bài 1 trang 35 Toán 7 Tập 2: Cho hai đa thức P(x) = -3x⁴ - 8x² + 2x và Q(x) = 5x³ - 3x² + 4x - 6.

Hãy tính P(x) + Q(x) và P(x) - Q(x).

Lời giải:

P(x) + Q(x) = (-3x⁴ - 8x² + 2x) + (5x³ - 3x² + 4x - 6)

P(x) + Q(x) = -3x⁴ - 8x² + 2x + 5x³ - 3x² + 4x - 6

P(x) + Q(x) = -3x⁴ + 5x³ + (-8x² - 3x²) + (2x + 4x) - 6

P(x) + Q(x) = -3x⁴ + 5x³ - 11x² + 6x - 6

P(x) - Q(x) = (-3x⁴ - 8x² + 2x) - (5x³ - 3x² + 4x - 6)

P(x) - Q(x) = -3x⁴ - 8x² + 2x - 5x³ + 3x² - 4x + 6

P(x) - Q(x) = -3x⁴ - 5x³ + (-8x² + 3x²) + (2x - 4x) + 6

P(x) - Q(x) = -3x⁴ - 5x³ - 5x² - 2x + 6

Vậy P(x) + Q(x) = -3x⁴ + 5x³ - 11x² + 6x - 6; P(x) - Q(x) = -3x⁴ - 5x³ - 5x² - 2x + 6.

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 2 trang 35 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Bài 2 trang 35 Toán 7 Tập 2: Cho đa thức M(x) = 7x³ - 2x² + 8x + 4.

Tìm đa thức N(x) sao cho M(x) + N(x) = 3x² - 2x.

Lời giải:

Do M(x) + N(x) = 3x² - 2x nên N(x) = 3x² - 2x - M(x)

N(x) = 3x² - 2x - (7x³ - 2x² + 8x + 4)

N(x) = 3x² - 2x - 7x³ + 2x² - 8x - 4

N(x) = -7x³ + (3x² + 2x²) + (-2x - 8x) - 4

N(x) = -7x³ + 5x² - 10x - 4

Vậy N(x) = -7x³ + 5x² - 10x - 4.

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 3 trang 36 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Bài 3 trang 36 Toán 7 Tập 2: Cho đa thức A(y) = -5y⁴ - 4y² + 2y + 7.

Tìm đa thức B(y) sao cho B(y) - A(y) = 2y³ - 9y² + 4y.

Lời giải:

Do B(y) - A(y) = 2y³ - 9y² + 4y nên B(y) = A(y) + 2y³ - 9y² + 4y

B(y) = (-5y⁴ - 4y² + 2y + 7) + 2y³ - 9y² + 4y

B(y) = -5y⁴ - 4y² + 2y + 7 + 2y³ - 9y² + 4y

B(y) = -5y⁴ + 2y³ + (-4y² - 9y²) + (2y + 4y) + 7

B(y) = -5y⁴ + 2y³ -13y² + 6y + 7

Vậy B(y) = -5y⁴ + 2y³ -13y² + 6y + 7.

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 4 trang 36 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

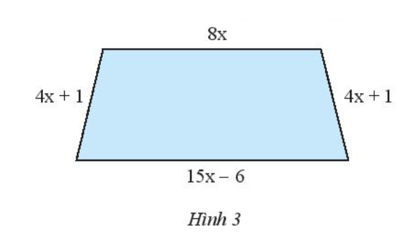
Bài 4 trang 36 Toán 7 Tập 2: Viết biểu thức biểu thị chu vi của hình thang cân trong Hình 3:

Lời giải:

Biểu thức biểu thị chu vi của hình thang cân là:

8x + 4x + 1 + 15x - 6 + 4x + 1

= (8x + 4x + 15x + 4x) + (1 - 6 + 1)

= 31x - 4

Vậy biểu thức biểu thị chu vi của hình thang cân là 31x - 4.

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 5 trang 36 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

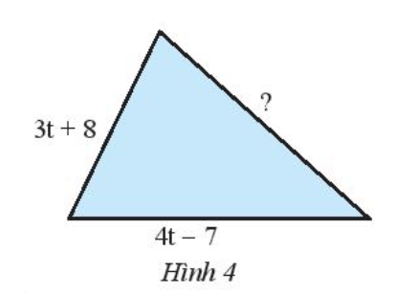
Bài 5 trang 36 Toán 7 Tập 2: Cho tam giác (Hình 4) có chu vi bằng 12t - 3. Tìm cạnh chưa biết của tam giác đó.

Lời giải:

Độ dài cạnh còn lại của tam giác bằng:

12t - 3 - (3t + 8) - (4t - 7)

= 12t - 3 - 3t - 8 - 4t + 7

= (12t - 3t - 4t) + (-3 - 8 + 7)

= 5t - 4

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 6 trang 36 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Bài 6 trang 36 Toán 7 Tập 2: Cho ba đa thức P(x) = 9x⁴ - 3x³ + 5x - 1; Q(x) = -2x³ - 5x² + 3x - 8;

R(x) = -2x⁴ + 4x² + 2x - 10.

Tính P(x) + Q(x) + R(x) và P(x) - Q(x) - R(x).

Lời giải:

P(x) + Q(x) + R(x) = (9x⁴ - 3x³ + 5x - 1) + (-2x³ - 5x² + 3x - 8) + (-2x⁴ + 4x² + 2x - 10)

= 9x⁴ - 3x³ + 5x - 1 - 2x³ - 5x² + 3x - 8 - 2x⁴ + 4x² + 2x - 10

= (9x⁴ - 2x⁴) + (-3x³ - 2x³) + (-5x² + 4x²) + (5x + 3x + 2x) + (-1 - 8 - 10)

= 7x⁴ - 5x³ - x² + 10x - 19

P(x) - Q(x) - R(x) = (9x⁴ - 3x³ + 5x - 1) - (-2x³ - 5x² + 3x - 8) - (-2x⁴ + 4x² + 2x - 10)

= 9x⁴ - 3x³ + 5x - 1 + 2x³ + 5x² - 3x + 8 + 2x⁴ - 4x² - 2x + 10

= (9x⁴ + 2x⁴) + (-3x³ + 2x³) + (5x² - 4x²) + (5x - 3x - 2x) + (-1 + 8 + 10)

= 11x⁴ - x³ + x² + 17

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 7 trang 36 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Bài 7 trang 36 Toán 7 Tập 2: Cho đa thức P(x) = x³ - 4x² + 8x - 2. Hãy viết P(x) thành tổng của hai đa thức bậc bốn.

Lời giải:

Đặt A(x) = x⁴ + x³ - 4x².

Khi đó P(x) = A(x) + B(x).

Suy ra B(x) = P(x) - A(x)

B(x) = (x³ - 4x² + 8x - 2) - (x⁴ + x³ - 4x²)

B(x) = x³ - 4x² + 8x - 2 - x⁴ - x³ + 4x²

B(x) = -x⁴ + (x³ - x³) + (-4x² + 4x²) + 8x - 2

B(x) = -x⁴ + 8x - 2.

Vậy P(x) = (x⁴ + x³ - 4x²) + (-x⁴ + 8x - 2).

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 8 trang 36 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

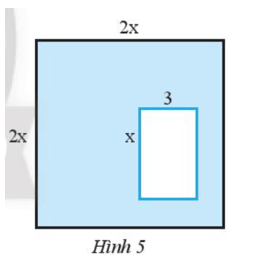
Bài 8 trang 36 Toán 7 Tập 2: Cho hình vuông cạnh 2x và bên trong là hình chữ nhật có độ dài hai cạnh là x và 3 (Hình 5).

Tìm đa thức theo biến x biểu thị diện tích của phần được tô màu xanh.

Lời giải:

Biểu thức biểu thị diện tích hình vuông là: 2x . 2x = 4x².

Biểu thức biểu thị diện tích hình chữ nhật là: 3x.

Biểu thức biểu thị diện tích của phần được tô màu xanh là: 4x² - 3x.

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 9 trang 36 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Bài 9 trang 36 Toán 7 Tập 2:

a) Thực hiện phép tính: (3x - 1) + [(2x² + 5x) + (4 - 3x)].

b) Cho A = 4x + 2, C = 5 - 3x². Tìm đa thức B sao cho A + B = C.

Lời giải:

a) (3x - 1) + [(2x² + 5x) + (4 - 3x)]

= 3x - 1 + 2x² + 5x + 4 - 3x

= 2x² + (3x + 5x - 3x) + (-1 + 4)

= 2x² + 5x + 3

b) Do A + B = C nên B = C - A

B = 5 - 3x² - (4x + 2)

B = 5 - 3x² - 4x - 2

B = -3x² - 4x + (5 - 2)

B = -3x² - 4x + 3

Vậy B = -3x² - 4x + 3.

Lời giải bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Sách bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Với giải sách bài tập Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 3.

Giải SBT Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Giải SBT Toán 7 trang 30 Tập 2

Vở thực hành Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

Với giải vở thực hành Toán lớp 7 Bài 3: Phép cộng và phép trừ đa thức một biến sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài 3.

Giải vở thực hành Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến - Chân trời sáng tạo

B. Câu hỏi trắc nghiệm

Chọn phương án đúng trong mỗi câu sau:

Giải VTH Toán 7 trang 22 Tập 2

Phép cộng và phép trừ đa thức một biến (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

Với tóm tắt lý thuyết Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến hay nhất, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Phép cộng và phép trừ đa thức một biến (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

Lý thuyết Phép cộng và phép trừ đa thức một biến

1. Phép cộng hai đa thức một biến

Để cộng hai đa thức một biến, ta làm một trong hai cách sau:

- Cách 1: Nhóm các đơn thức cùng lũy thừa của biến rồi thực hiện phép cộng.

- Cách 2: Sắp xếp các đơn thức của hai đa thức cùng theo lũy thừa giảm dần (hoặc tăng dần) của biến rồi đặt phép tính theo cột dọc tương ứng sao cho lũy thừa giống nhau ở hai đa thức thẳng cột với nhau rồi thực hiện cộng theo cột.

Ví dụ: Cho M(x) = 6x² – 5x + 1 và N(x) = –3x² – 2x – 7. Hãy tính tổng của M(x) và N(x) bằng hai cách.

Hướng dẫn giải:

Cách 1: M(x) + N(x) = 6x² – 5x + 1 + (–3x² – 2x – 7)

= 6x² – 5x + 1 – 3x² – 2x – 7

= (6x² –3x²) + (– 5x – 2x) + (1 – 7)

= 3x² – 7x – 6

Cách 2: Cộng theo cột dọc

$\frac{\begin{array}{c}{+}_{}M\left(x\right)=6x^2–5x+1\\ N\left(x\right)=–3x^2–2x–7\end{array}}{M\left(x\right)+N\left(x\right){=}^{}3x^2-7x-6}$

2. Phép trừ hai đa thức một biến

Để trừ hai đa thức một biến, ta làm một trong hai cách sau:

- Cách 1:Nhóm các đơn thức cùng lũy thừa của biến rồi thực hiện phép trừ.

- Cách 2: Sắp xếp các đơn thức của hai đa thức cùng theo lũy thừa giảm dần (hoặc tăng dần) của biến rồi đặt phép tính theo cột dọc tương ứng sao cho lũy thừa giống nhau ở hai đa thức thẳng cột với nhau rồi thực hiện trừ theo cột.

Ví dụ: Cho P(x) = 9x² – 2x + 4 và Q(x) = –x² + 3x – 7. Hãy tính hiệu của P(x) và Q(x) bằng hai cách.

Hướng dẫn giải:

Cách 1: Nhóm các đơn thức cùng lũy thừa của biến rồi thực hiện phép tính.

P(x) + Q(x) = 9x² – 2x + 4 – (–x² + 3x – 7)

= 9x² – 2x + 4 + x² – 3x + 7

= (9x² + x²) + (– 2x – 3x) + (4 + 7)

= 10x² – 5x + 11

Cách 2: Đặt phép tính theo cột dọc.

$\frac{\begin{array}{c}\_P\left(x\right)=9x^2–2x+4\\ Q\left(x\right)=–x^2+3x-7\end{array}}{P\left(x\right)-Q\left(x\right)=10x^2-5x+11}$

3. Tính chất của phép cộng đa thức một biến

Tính chất: Cho A, B, C là các đa thức một biến với cùng một biến số.

-Tính chất giao hoán: A + B = B + A;

-Tính chất kết hợp: A + (B + C) = (A + B) + C.

Ví dụ: Thực hiện phép tính (2x – 1) + [(x² + 3x) + (2 – 2x)].

Hướng dẫn giải:

(2x – 1) + [(x² + 3x) + (2 – 2x)] = (2x – 1) + [(2 – 2x) + (x² + 3x)]

= [(2x – 1) + (2 – 2x)] + (x² + 3x)

= (2x – 1 + 2 – 2x) + (x² + 3x)

= 1 + (x² + 3x)

= x² + 3x + 1.

Bài tập Phép cộng và phép trừ đa thức một biến

Bài 1. Cho hai đa thức f(x) = 3x² + 2x − 5 và g(x) = −3x² − 2x + 2. Tính h(x) = f(x) + g(x) và tìm bậc của h(x).

Hướng dẫn giải:

Ta có: h(x) = f (x) + g (x)

= (3x² + 2x− 5) + (−3x² − 2x + 2)

= 3x² + 2x − 5 − 3x² − 2x + 2

= (3x² − 3x²) + (2x − 2x) + (−5 + 2) = −3.

Vậy h(x) = −3 và bậc của h(x) là 0.

Bài 2:Cho hai đa thức f(x) = 5x⁴ + x³ − x² + 1 và g(x) = −5x⁴ − x² + 2.

Tính k(x) = f(x) − g(x) và tìm bậc của k(x).

Hướng dẫn giải:

Ta có: k(x) = f(x) − g(x)

= (5x⁴ + x³ − x² + 1) −(−5x⁴ − x² + 2)

= 5x⁴ + x³ − x² + 1 + 5x⁴ + x² − 2

= (5x⁴ + 5x⁴) + x³ + (−x² +x²) + (1 − 2)

= 10x⁴ + x³ – 1.

Vậy k(x) =10x⁴ + x³ − 1và bậc của k(x) là 4.

Bài 3. Cho f (x) = x⁵ − 3x⁴ + x² − 5 và g (x) = 2x⁴ +7x³ − x² + 6. Tính hiệu f(x) − g(x) rồi sắp xếp kết quả theo lũy thừa tăng dần của biến.

Hướng dẫn giải:

Ta có: f(x) − g(x) = (x⁵ − 3x⁴ + x² −5) – (2x⁴ + 7x³ − x² + 6)

= x⁵ − 3x⁴ + x² − 5 – 2x⁴ – 7x³ + x² – 6

= x⁵ + (−3x⁴ − 2x⁴) – 7x³ + (x² + x²) + (− 5− 6)

= x⁵ − 5x⁴ − 7x³ + 2x² −11.

Vậy hiệu f(x) − g(x) và sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:

11 + 2x² −7x³ − 5x⁴ + x⁵.

Bài 4: Tìm đa thức h(x) biết f(x) − h(x) = g(x).

Trong đó: f(x) = x² + x + 1; g(x) = 4 − 2x³ + x⁴ + 7x⁵.

Hướng dẫn giải:

Ta có: f(x) − h(x) = g(x).

Suy ra: h(x) = f(x)− g(x).

= (x² + x + 1) – (4 − 2x³ + x⁴ + 7x⁵)

= x² + x + 1 – 4 + 2x³ – x⁴ – 7x⁵

= −7x⁵− x⁴ + 2x³ + x² + x – 3.

Vậy h(x) = −7x⁵− x⁴+ 2x³ + x² + x – 3.

Học tốt Phép cộng và phép trừ đa thức một biến

Các bài học để học tốt Phép cộng và phép trừ đa thức một biến Toán lớp 7 hay khác:

15 Bài tập Phép cộng và phép trừ đa thức một biến (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Phép cộng và phép trừ đa thức một biến Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Phép cộng và phép trừ đa thức một biến (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 7

Xem thử

Chỉ từ 150k mua trọn bộ trắc nghiệm Toán 7 Chân trời sáng tạo (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: