Với giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán Hình 7 Bài 5.

Giải Toán 7 Chân trời sáng tạo Bài 5: Đường trung trực của một đoạn thẳng

Hoạt động khởi động

Giải Toán 7 trang 67 Tập 2

Khởi động trang 67 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

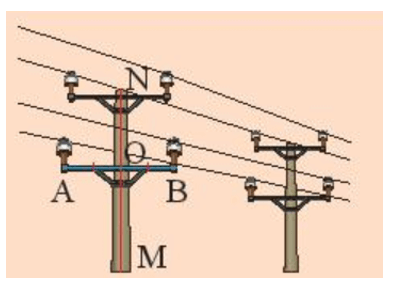
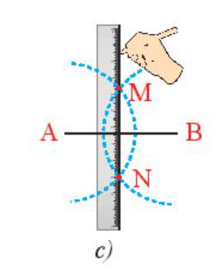
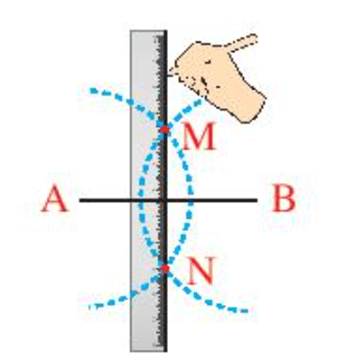
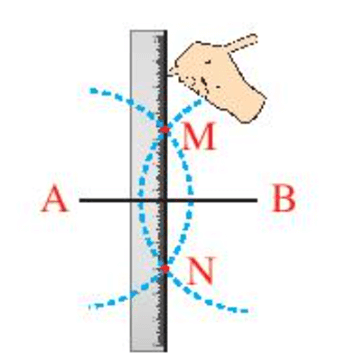
Khởi động trang 67 Toán 7 Tập 2: Cột điện MN vuông góc với thanh xà AB tại điểm nào của đoạn thẳng AB?

Lời giải:

Cột điện MN vuông góc với thanh xà AB tại điểm O của đoạn thẳng AB.

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Khám phá 1 trang 67 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

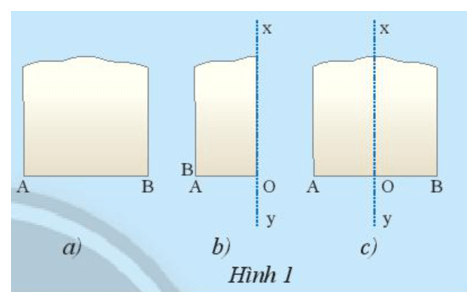
Khám phá 1 trang 67 Toán 7 Tập 2: Lấy một mảnh giấy như trong Hình 1a, gọi một mép cắt là đoạn thẳng AB. Sau đó gấp mảnh giấy sao cho điểm A trùng với điểm B (Hình 1b).

Theo em nếp gấp xy có vuông góc với đoạn AB tại trung điểm hay không? Vì sao?

Lời giải:

Ta thấy khi gấp giấy điểm A trùng với điểm B nên O là trung điểm của AB.

Ngoài ra nếp gấp vuông góc với đoạn AB.

Do đó nếp gấp xy vuông góc với đoạn AB tại trung điểm của AB.

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Thực hành 1 trang 67 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

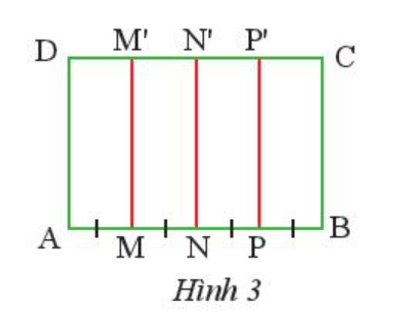
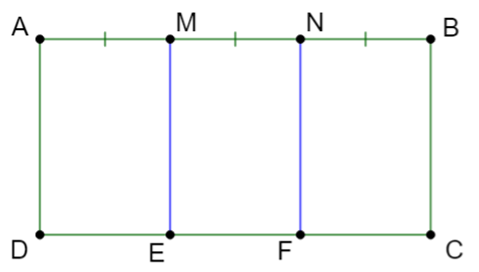
Thực hành 1 trang 67 Toán 7 Tập 2: Cho hình chữ nhật ABCD, trên cạnh AB lấy các điểm M, N, P và trên cạnh DC lấy các điểm M’, N’, P’. Cho biết AM = MN = NP = PB và MM’, NN’, PP’ đều song song với BC (Hình 3). Tìm đường trung trực của mỗi đoạn thẳng AB, AN và NB.

Lời giải:

Do ABCD là hình chữ nhật nên MM’ $\perp$ AB, NN’ $\perp$ AB, PP’ $\perp$ AB.

Ta có AN = AM + MN; NB = NP + PB.

Do AM = MN = NP = PB nên AN = NB và N nằm giữa AB do đó N là trung điểm của AB.

Khi đó NN’ $\perp$ AB và N là trung điểm của AB nên đường trung trực của đoạn AB là NN’.

Do AM = MN và M nằm giữa AN nên M là trung điểm của AN.

Do MM’ $\perp$ AN và M là trung điểm của AN nên đường trung trực của đoạn AN là MM’.

Do NP = PB và P nằm giữa N và B nên P là trung điểm của NB.

Do PP’ $\perp$ NB và P là trung điểm của NB nên đường trung trực của đoạn NB là PP’.

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Vận dụng 1 trang 67 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

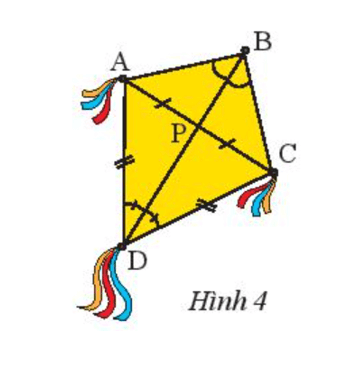
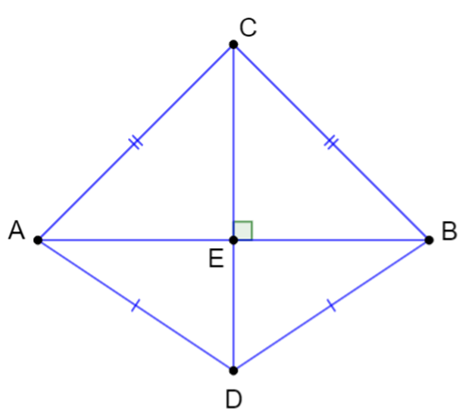
Vận dụng 1 trang 67 Toán 7 Tập 2: Trong Hình 4, hãy cho biết BD có là đường trung trực của đoạn thẳng AC hay không. Tại sao?

Lời giải:

Do DA = DC (theo giả thiết) nên D nằm trên đường trung trực của đoạn thẳng AC (1).

Suy ra DP $\perp$ AC.

Xét △BPA vuông tại P và △BPC vuông tại P có:

BP chung.

PA = PC (theo giả thiết).

Suy ra △BPA = △BPC (2 cạnh góc vuông).

Do đó BA = BC (2 cạnh tương ứng).

Suy ra B nằm trên đường trung trực của AC (2).

Từ (1) và (2) suy ra BD là đường trung trực của đoạn thẳng AC.

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Khám phá 2 trang 68 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

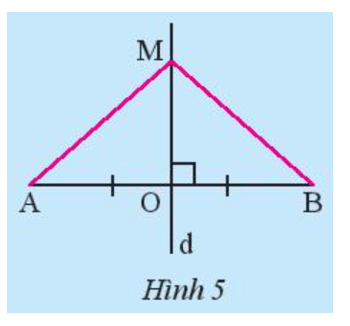
Khám phá 2 trang 68 Toán 7 Tập 2: Cho đoạn thẳng AB có O là trung điểm và d là đường trung trực. Lấy điểm M tùy ý thuộc d (Hình 5).

Chứng minh rằng hai tam giác MOA và MOB bằng nhau, từ đó suy ra MA = MB.

Lời giải:

Do d là đường trung trực của AB nên d $\perp$ AB và O là trung điểm của AB.

Khi đó OA = OB.

Xét △MOA vuông tại O và △MOB vuông tại O có:

OA = OB (chứng minh trên).

OM chung.

Do đó $\Delta MOA=\Delta MOB$(2 cạnh góc vuông).

Suy ra MA = MB (2 cạnh tương ứng).

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Thực hành 2 trang 69 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

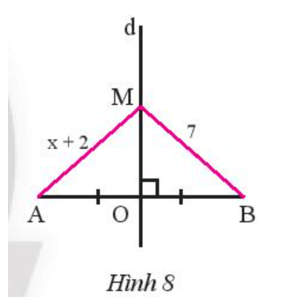
Thực hành 2 trang 69 Toán 7 Tập 2: Trong Hình 8, cho biết d là đường trung trực của đoạn thẳng AB, điểm M thuộc đường thẳng d, MA = x + 2 và MB = 7. Tính x.

Lời giải:

Do M thuộc đường trung trực của đoạn thẳng AB nên MA = MB.

Do đó x + 2 = 7 suy ra x = 5.

Vậy x = 5.

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Vận dụng 2 trang 69 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

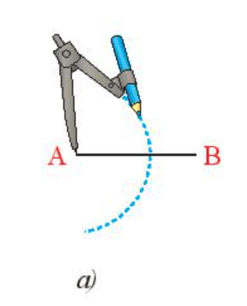
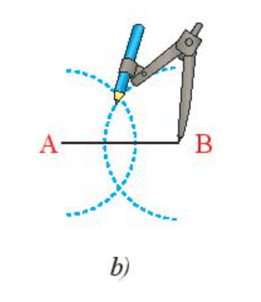
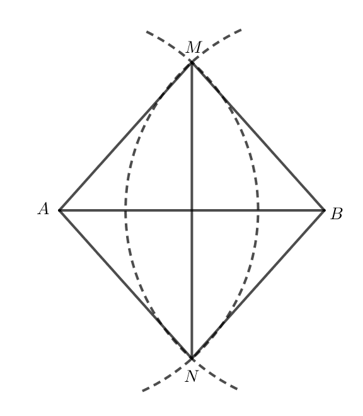
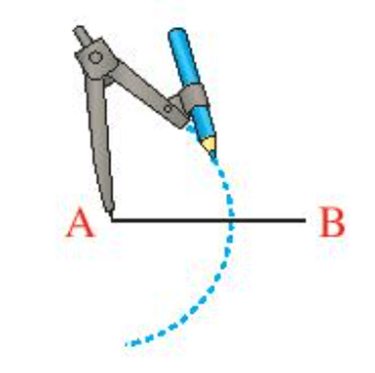
Vận dụng 2 trang 69 Toán 7 Tập 2: Dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa theo hướng dẫn sau:

- Lấy A làm tâm vẽ cung tròn bán kính lớn hơn $\frac{1}{2}$AB (Hình 9a).

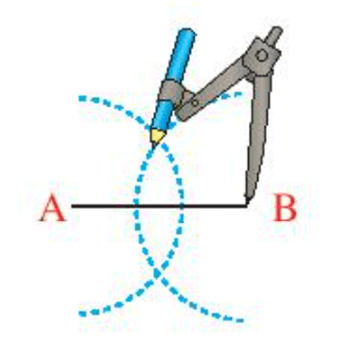
- Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên (Hình 9b).

- Hai cung tròn này cắt nhau tại M và N (Hình 9c). Dùng thước vẽ đường thẳng MN.

Hãy chứng minh đường thẳng MN chính là đường trung trực của đoạn thẳng AB.

Lời giải:

Giả sử độ dài đoạn thẳng AB là 4 cm.

Thực hiện vẽ theo hướng dẫn của đề bài với bán kính cung tròn tại A và B là 3 cm.

Ta thu được hình sau:

Hai cung tròn tại A và B có bán kính 3 cm cắt nhau tại M và N nên

MA = MB = NA = NB = 3 cm.

Do MA = MB nên M nằm trên đường trung trực của đoạn thẳng AB.

Do NA = NB nên N nằm trên đường trung trực của đoạn thẳng AB.

Vậy MN là đường trung trực của đoạn AB.

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Bài 1 trang 70 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

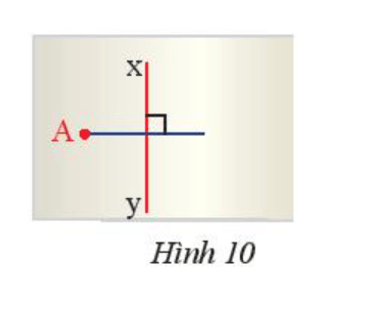
Bài 1 trang 70 Toán 7 Tập 2: Hình 10 minh họa một tờ giấy có hình vẽ đường trung trực xy của đoạn thẳng AB mà hình ảnh điểm B bị nhòe mất. Hãy nêu cách xác định điểm B.

Lời giải:

Do xy là đường trung trực của đoạn thẳng AB nên xy vuông góc với AB tại trung điểm của AB.

Gọi O là giao điểm của xy và AB.

Khi đó về bên phải điểm O, trên đường thẳng qua O và vuông góc với xy, ta xác định một điểm sao cho khoảng cách từ điểm đó đến điểm O bằng độ dài đoạn OA.

Điểm đó chính là điểm B.

Ta có hình vẽ sau:

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Bài 2 trang 70 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

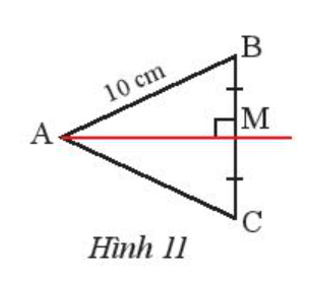
Bài 2 trang 70 Toán 7 Tập 2: Quan sát Hình 11, cho biết M là trung điểm của BC, AM vuông góc với BC và AB = 10 cm. Tính AC.

Lời giải:

Do M là trung điểm của BC và AM vuông góc với BC tại M nên AM là đường trung trực của BC.

Khi đó AB = AC.

Vậy AC = 10 cm.

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Bài 3 trang 70 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

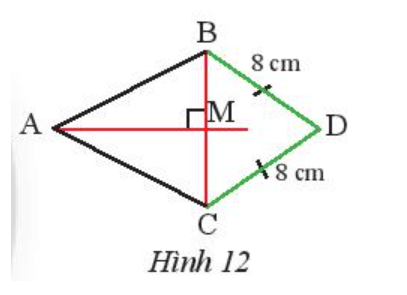
Bài 3 trang 70 Toán 7 Tập 2: Quan sát Hình 12, cho biết AM là đường trung trực của đoạn thẳng BC và DB = DC = 8 cm. Chứng minh rằng ba điểm A, M, D thẳng hàng.

Lời giải:

Do DB = DC = 8 cm nên D nằm trên đường trung trực của đoạn BC.

Mà AM là đường trung trực của đoạn BC hay D nằm trên đường thẳng AM.

Do đó A, M, D thẳng hàng.

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Bài 4 trang 70 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

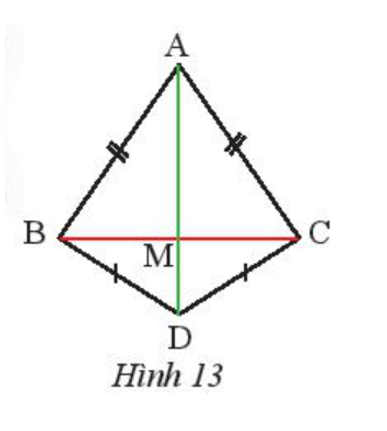
Bài 4 trang 70 Toán 7 Tập 2: Quan sát Hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC.

Lời giải:

Do AB = AC nên A nằm trên đường trung trực của đoạn BC.

Do DB = DC nên D nằm trên đường trung trực của đoạn BC.

Khi đó AD là đường trung trực của đoạn BC.

Do đó AD vuông góc với BC tại trung điểm của BC.

Mà AD cắt BC tại M nên M là trung điểm của BC.

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Bài 5 trang 70 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

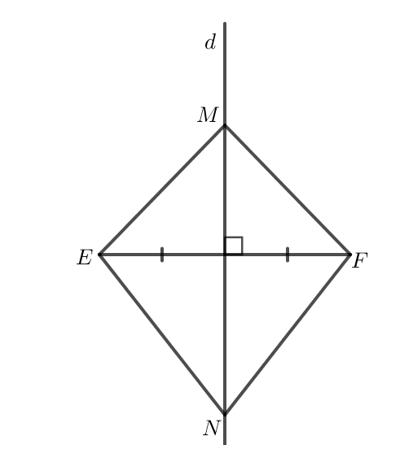
Bài 5 trang 70 Toán 7 Tập 2: Cho hai điểm M và N nằm trên đường trung trực d của đoạn thẳng EF.

Chứng minh rằng $\Delta EMN=\Delta FMN$.

Lời giải:

Do M và N nằm trên đường trung trực của đoạn thẳng EF nên ME = MF và NE = NF.

Xét $\Delta EMN$và $\Delta FMN$có:

ME = MF (chứng minh trên).

NE = NF (chứng minh trên).

MN chung.

Do đó $\Delta EMN=\Delta FMN$(c - c - c).

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Bài 6 trang 70 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

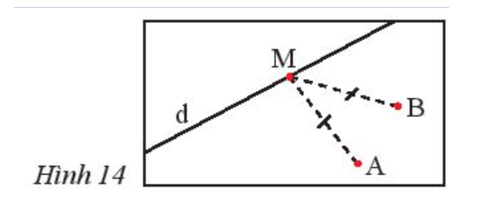
Bài 6 trang 70 Toán 7 Tập 2: Trên bản đồ quy hoạch một khu dân cư có một con đường d và hai điểm dân cư A và B (Hình 14). Hãy tìm bên đường một địa điểm M để xây dựng một trạm y tế sao cho trạm y tế cách đều hai điểm dân cư.

Lời giải:

Trạm y tế cách đều hai điểm dân cư tức MA = MB.

Khi đó M nằm trên đường trung trực của AB.

Mà M nằm trên đường thẳng d nên M là giao điểm của d và đường trung trực của AB.

Lời giải bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay, chi tiết khác:

Sách bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

Với giải sách bài tập Toán 7 Bài 5: Đường trung trực của một đoạn thẳng sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 5.

Giải SBT Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

Giải SBT Toán 7 trang 55 Tập 2

Vở thực hành Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

Với giải vở thực hành Toán lớp 7 Bài 5: Đường trung trực của một đoạn thẳng sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài 5.

Giải vở thực hành Toán 7 Bài 5: Đường trung trực của một đoạn thẳng - Chân trời sáng tạo

B. Câu hỏi trắc nghiệm

Chọn phương án đúng trong mỗi câu sau:

Giải VTH Toán 7 trang 47 Tập 2

Đường trung trực của một đoạn thẳng (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

Với tóm tắt lý thuyết Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hay nhất, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Đường trung trực của một đoạn thẳng (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

Lý thuyết Đường trung trực của một đoạn thẳng

1. Đường trung trực của một đoạn thẳng

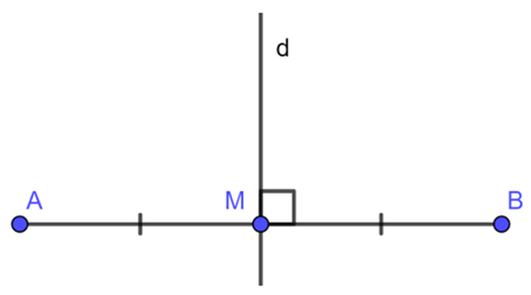
Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm của đó.

Ví dụ:Trong hình dưới đây, đường thẳng d là đường trung trực của đoạn thẳng AB vì d vuông góc với AB lại trung điểm M của AB.

2. Tính chất của đường trung trực

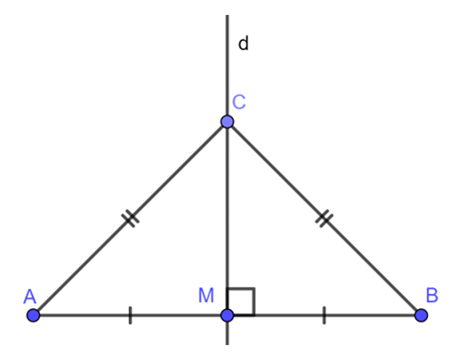
Định lí 1: Điểm nằm trên trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Ví dụ: Trong hình vẽ dưới đây có d là đường thẳng trung trực của đoạn thẳng AB.

Với điểm C $\in$ d thì ta suy ra được CA = CB.

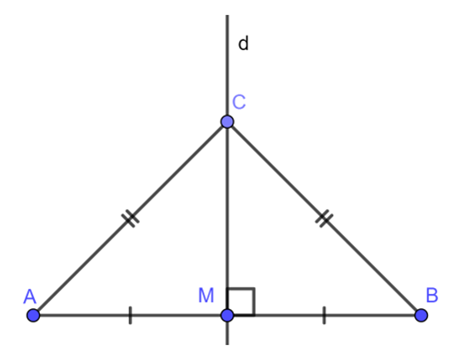
Định lí 2: Điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Ví dụ: Trong hình vẽ dưới đây có d là đường trung trực của đoạn thẳng AB.

Ta có: CA = CB suy ra điểm C thuộc đường thẳng d.

Chú ý: Các bước dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa:

(1) Khi vẽ hai cung tròn trên, ta phải lấy bán kính lớn hơn $\frac{1}{2}$AB thì hai cung tròn đó mới có hai điểm chung.

Ví dụ:

+ Lấy A làm tâm vẽ cung tròn bán kính lớn hơn $\frac{1}{2}$AB (như hình vẽ dưới đây)

+ Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên (như hình vẽ dưới đây)

+ Hai cung tròn này cắt nhau tại M và N (như hình vẽ dưới đây). Dùng thức vẽ đường thẳng MN. Khi đó MN là đường trung trực đoạn thẳng AB.

Chứng minh:

Hai cung tròn có cùng bán kính và cắt nhau tại M và N nên ta suy ra được MA = MB = NA = NB.

Khi đó, M và N là hai điểm cách đều hai đầu mút A và B của đoạn thẳng AB nên suy M, N nằm trên đường trung trực của đoạn thẳng AB (Theo định lí 2).

Vậy suy ra MN là đường thẳng trung trực của đoạn thẳng AB.

(2) Giao điểm của đường thẳng MN với đoạn thẳng AB là trung điểm của đoạn thẳng AB nên cách vẽ trên cũng là cách dựng trung điểm của đoạn thẳng bằng thước và compa.

Chứng minh: Từ chú ý trên ta chứng minh được MN là đường trung trực của đoạn thẳng AB khi đó MN vuông góc với AB tại trung điểm của AB. Nên suy ra MN giao với AB tại trung điểm của đoạn thẳng AB.

Bài tập Đường trung trực của một đoạn thẳng

Bài 1: Cho hình chữ nhật ABCD, trên cạnh AB lấy các điểm M, N và trên cạnh DC lấy các điểm E, F. Cho biết AM = MN = NB và ME, NF đều song song với AD. Tìm đường trung trực của mỗi đoạn thẳng AN và MB.

Hướng dẫn giải

Xét hình chữ nhật ABCD có AB vuông góc với AD.

Mà ME và NF đều song song với AD nên suy ra ME và NF đều vuông góc với AB.

+) Xét ME vuông góc với đoạn thẳng AB nên cũng vuông góc với đoạn thẳng AN tại trung điểm M của AN nên ME là đường trung trực của đoạn thẳng AM.

+) Xét NF vuông góc với đoạn thẳng AB nên cũng vuông góc với đoạn thẳng MB tại trung điểm N của MB nên NF là đường trung trực của đoạn thẳng MB.

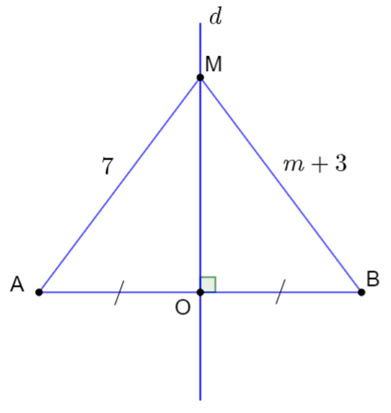
Bài 2: Trong hình vẽ dưới đây, cho d là đường trung trực của đoạn thẳng AB, điểm M thuộc đường thẳng d, MA = 7 và MB = m + 3. Tính m.

Hướng dẫn giải

Áp dụng định lí 1, với điểm M nằm trên đường thẳng trung trực của đoạn thẳng AB thì M cách đều hai đầu mút A, B nên suy ra

Điểm M nằm trên đường thẳng trung trực của đoạn thẳng AB thì M cách đều hai đầu mút A, B nên suy ra

MA = MB

Hay 7 = m + 3

Do đó m = 7 - 3 = 4

Vây giá trị của m là 4.

Bài 3: Cho C, D là hai điểm nằm trên đường trung trực của đoạn thẳng AB. CD giao AB tại E. Chứng minh hai tam giác CAD và CBD bằng nhau.

Hướng dẫn giải

Hai điểm C, D nằm trên đường trung trực của đoạn thẳng AB nên lần lượt cách đều hai đầu mút A và B.

Suy ra CA = CB và DA = DB

Xét hai tam giác CAD và CBD có

CA = CB (cmt)

DA = DB (cmt)

CD: cạnh chung

Suy ra ∆CAD = ∆CBD (c.c.c).

Học tốt Đường trung trực của một đoạn thẳng

Các bài học để học tốt Đường trung trực của một đoạn thẳng Toán lớp 7 hay khác:

15 Bài tập Đường trung trực của một đoạn thẳng (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Đường trung trực của một đoạn thẳng Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Đường trung trực của một đoạn thẳng (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 7

Xem thử

Chỉ từ 150k mua trọn bộ trắc nghiệm Toán 7 Chân trời sáng tạo (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: