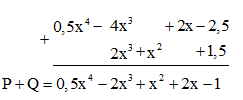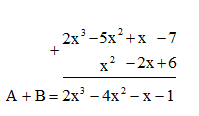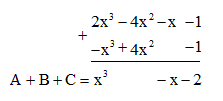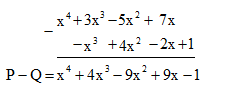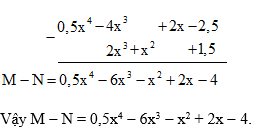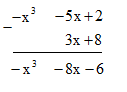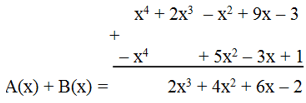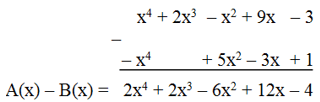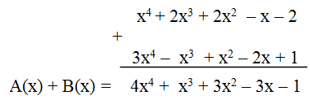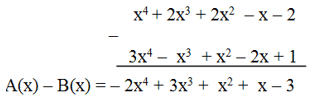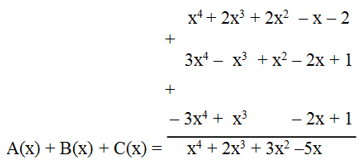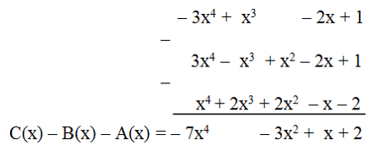Với giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán 7 Bài 26.

Giải Toán 7 Kết nối tri thức Bài 26: Phép cộng và phép trừ đa thức một biến

Video Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến - Cô Trần Thị Ngọc Anh (Giáo viên VietJack)

1. Cộng hai đa thức một biến

Giải Toán 7 trang 32 Tập 2

Câu hỏi trang 32 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

Câu hỏi trang 32 Toán 7 Tập 2: Tìm tổng của hai đa thức: x³ - 5x + 2 và x³ - x² + 6x - 4.

Lời giải:

Tổng của hai đa thức x³ - 5x + 2 và x³ - x² + 6x - 4 là:

x³ - 5x + 2 + x³ - x² + 6x - 4

= (x³ + x³) - x² + (-5x + 6x) + (2 - 4)

= 2x³ - x² + x + (-2)

= 2x³ - x² + x - 2.

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Luyện tập 1 trang 32 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

Luyện tập 1 trang 32 Toán 7 Tập 2: Cho hai đa thức M = 0,5x⁴ - 4x³ + 2x - 2,5 và N = 2x³ + x² + 1,5

Hãy tính tổng M + N (trình bày theo hai cách).

Lời giải:

Cách 1. Bỏ dấu ngoặc.

M + N = (0,5x⁴ - 4x³ + 2x - 2,5) + (2x³ + x² + 1,5)

M + N = 0,5x⁴ - 4x³ + 2x - 2,5 + 2x³ + x² + 1,5

M + N = 0,5x⁴ + (-4x³ + 2x³) + x² + 2x + (-2,5 + 1,5)

M + N = 0,5x⁴ + (-2x³) + x² + 2x + (-1)

M + N = 0,5x⁴ - 2x³ + x² + 2x - 1.

Cách 2. Đặt phép tính.

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Vận dụng 1 trang 32 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

Vận dụng 1 trang 32 Toán 7 Tập 2: Đặt tính cộng để tìm tổng của ba đa thức sau:

A = 2x³ - 5x² + x - 7;

B = x² - 2x + 6;

C = -x³ + 4x² - 1.

Lời giải:

Thực hiện tính A + B ta được:

Thực hiện tính A + B + C ta được:

Vậy A + B + C = x³ - x - 2.

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

HĐ1 trang 32 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

HĐ1 trang 32 Toán 7 Tập 2: Cho hai đa thức P = x⁴ + 3x³ - 5x² + 7x và Q = -x³ + 4x² - 2x + 1

Đối với phép trừ: P - Q = (x⁴ + 3x³ - 5x² + 7x) - (-x³ + 4x² - 2x + 1), ta cũng có hai cách trình bày, tương tự như phép cộng hai đa thức.

Tìm hiệu P - Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.

Lời giải:

P - Q = (x⁴ + 3x³ - 5x² + 7x) - (-x³ + 4x² - 2x + 1)

P - Q = x⁴ + 3x³ - 5x² + 7x + x³ - 4x² + 2x - 1

P - Q = x⁴ + (3x³ + x³) + (-5x² - 4x²) + (7x + 2x) - 1

P - Q = x⁴ + 4x³ + (-9x²) + 9x - 1

P - Q = x⁴ + 4x³ -9x² + 9x - 1

Vậy P - Q = x⁴ + 4x³ -9x² + 9x - 1.

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

HĐ2 trang 32 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

HĐ2 trang 32 Toán 7 Tập 2: Cho hai đa thức P = x⁴ + 3x³ - 5x² + 7x và Q = -x³ + 4x² - 2x + 1

Đối với phép trừ: P - Q = (x⁴ + 3x³ - 5x² + 7x) - (-x³ + 4x² - 2x + 1), ta cũng có hai cách trình bày, tương tự như phép cộng hai đa thức.

Tìm hiệu P - Q bằng cách đặt tính trừ: đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau rồi trừ theo từng cột.

Lời giải:

Đặt phép tính ta được:

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Luyện tập 2 trang 32 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

Luyện tập 2 trang 32 Toán 7 Tập 2: Cho hai đa thức: M = 0,5x⁴ - 4x³ + 2x - 2,5 và N = 2x³ + x² + 1,5.

Hãy tính hiệu M - N (trình bày theo hai cách).

Lời giải:

Cách 1. Bỏ dấu ngoặc.

M - N = (0,5x⁴ - 4x³ + 2x - 2,5) - (2x³ + x² + 1,5)

M - N = 0,5x⁴ - 4x³ + 2x - 2,5 - 2x³ - x² - 1,5

M - N = 0,5x⁴ + (-4x³ - 2x³) - x² + 2x + (-2,5 - 1,5)

M - N = 0,5x⁴ + (-6x³) - x² + 2x + (-4)

M - N = 0,5x⁴ - 6x³ - x² + 2x - 4

Vậy M - N = 0,5x⁴ - 6x³ - x² + 2x - 4.

Cách 2. Đặt phép tính.

Vậy M - N = 0,5x⁴ - 6x³ - x² + 2x - 4.

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Vận dụng 2 trang 33 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

Vận dụng 2 trang 33 Toán 7 Tập 2:

Cho đa thức A = x⁴ - 3x² - 2x + 1. Tìm các đa thức B và C sao cho:

A + B = 2x⁵ + 5x³ - 2;

A - C = x³.

Lời giải:

Do A + B = 2x⁵ + 5x³ - 2 nên B = 2x⁵ + 5x³ - 2 - A

B = 2x⁵ + 5x³ - 2 - (x⁴ - 3x² - 2x + 1)

B = 2x⁵ + 5x³ - 2 - x⁴ + 3x² + 2x - 1

B = 2x⁵ - x⁴ + 5x³ + 3x² + 2x + (-2 - 1)

B = 2x⁵ - x⁴ + 5x³ + 3x² + 2x + (-3)

B = 2x⁵ - x⁴ + 5x³ + 3x² + 2x -3

Do A - C = x³ nên C = A - x³

C = x⁴ - 3x² - 2x + 1 - x³

C = x⁴ - x³ - 3x² - 2x + 1

Vậy B = 2x⁵ - x⁴ + 5x³ + 3x² + 2x -3; C = x⁴ - x³ - 3x² - 2x + 1.

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 7.12 trang 33 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

Bài 7.12 trang 33 Toán 7 Tập 2: Tìm tổng của hai đa thức sau bằng cách nhóm các hạng tử cùng bậc: x² - 3x + 2 và 4x³ - x² + x - 1.

Lời giải:

(x² - 3x + 2) + (4x³ - x² + x - 1)

= x² - 3x + 2 + 4x³ - x² + x - 1

= 4x³ + (x² - x²) + (-3x + x) + (2 - 1)

= 4x³ + (-2x) + 1

= 4x³ - 2x + 1.

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 7.13 trang 33 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

Bài 7.13 trang 33 Toán 7 Tập 2: Tìm hiệu sau theo cách đặt tính trừ: (-x³ - 5x + 2) - (3x + 8).

Lời giải:

Đặt phép tính ta được:

Vậy (-x³ - 5x + 2) - (3x + 8) = -x³ - 8x - 6.

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 7.14 trang 33 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

Bài 7.14 trang 33 Toán 7 Tập 2: Cho hai đa thức A = 6x⁴ - 4x³ + x - $\frac{1}{3}$và B = -3x⁴ - 2x³ - 5x² + x + $\frac{2}{3}$

Tính A + B và A - B.

Lời giải:

A + B = (6x⁴ - 4x³ + x - $\frac{1}{3}$) + (-3x⁴ - 2x³ - 5x² + x + $\frac{2}{3}$)

A + B = 6x⁴ - 4x³ + x - $\frac{1}{3}$+ (-3x⁴) - 2x³ - 5x² + x + $\frac{2}{3}$

A + B = (6x⁴ - 3x⁴) + (-4x³ - 2x³) - 5x² + (x + x) + $(\frac{2}{3}-\frac{1}{3})$

A + B = 3x⁴ + (-6x³) - 5x² + 2x + $\frac{1}{3}$

A + B = 3x⁴ - 6x³ - 5x² + 2x + $\frac{1}{3}$

A - B = (6x⁴ - 4x³ + x - $\frac{1}{3}$) - (-3x⁴ - 2x³ - 5x² + x + $\frac{2}{3}$)

A - B = 6x⁴ - 4x³ + x - $\frac{1}{3}$+ 3x⁴ + 2x³ + 5x² - x - $\frac{2}{3}$

A - B = (6x⁴ + 3x⁴) + (-4x³ + 2x³) + 5x² + (x - x) + $(-\frac{1}{3}-\frac{2}{3})$

A - B = 9x⁴ + (-2x³) + 5x² + (-1)

A - B = 9x⁴ - 2x³ + 5x² - 1

Vậy A + B = 3x⁴ - 6x³ - 5x² + 2x + $\frac{1}{3}$; A - B = 9x⁴ - 2x³ + 5x² - 1.

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 7.15 trang 33 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

Bài 7.15 trang 33 Toán 7 Tập 2: Cho các đa thức A = 3x⁴ - 2x³ - x + 1; B = -2x³ + 4x² + 5x và C = -3x⁴ + 2x² + 5

Tính A + B + C; A - B + C và A - B - C.

Lời giải:

A + B + C = (3x⁴ - 2x³ - x + 1) + (-2x³ + 4x² + 5x) + (-3x⁴ + 2x² + 5)

A + B + C = 3x⁴ - 2x³ - x + 1 + (-2x³) + 4x² + 5x + (-3x⁴) + 2x² + 5

A + B + C = (3x⁴ - 3x⁴) + (-2x³ - 2x³) + (4x² + 2x²) + (-x + 5x) + (1 + 5)

A + B + C = -4x³ + 6x² + 4x + 6.

A - B + C = (3x⁴ - 2x³ - x + 1) - (-2x³ + 4x² + 5x) + (-3x⁴ + 2x² + 5)

A - B + C = 3x⁴ - 2x³ - x + 1 + 2x³ - 4x² - 5x - 3x⁴ + 2x² + 5

A - B + C = (3x⁴ - 3x⁴) + (-2x³ + 2x³) + (-4x² + 2x²) + (-x - 5x) + (1 + 5)

A - B + C = -2x² + (-6x) + 6

A - B + C = -2x² - 6x + 6.

A - B - C = (3x⁴ - 2x³ - x + 1) - (-2x³ + 4x² + 5x) - (-3x⁴ + 2x² + 5)

A - B - C = 3x⁴ - 2x³ - x + 1 + 2x³ - 4x² - 5x + 3x⁴ - 2x² - 5

A - B - C = (3x⁴ + 3x⁴) + (-2x³ + 2x³) + (-4x² - 2x²) + (-x - 5x) + (1 - 5)

A - B - C = 6x⁴ + (-6x²) + (-6x) + (-4)

A - B - C = 6x⁴ - 6x² - 6x - 4.

Vậy A + B + C = -4x³ + 6x² + 4x + 6; A - B + C = -2x² - 6x + 6;

A - B - C = 6x⁴ - 6x² - 6x - 4.

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 7.16 trang 33 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

Bài 7.16 trang 33 Toán 7 Tập 2: Bạn Nam được phân công mua một số sách làm quà tặng trong buổi tổng kết cuối năm học của lớp. Nam dự định mua ba loại sách với giá bán như bảng sau. Giả sử Nam cần mua x cuốn sách khoa học, x + 8 cuốn sách tham khảo và x + 5 cuốn truyện tranh.

a) Viết các đa thức biểu thị số tiền Nam phải trả cho từng loại sách.

b) Tìm đa thức biểu thị tổng số tiền Nam phải trả để mua số sách đó.

Lời giải:

a) Số tiền Nam phải trả để mua sách khoa học là 21 500.x đồng.

Số tiền Nam phải trả để mua sách tham khảo là 12 500.(x + 8) đồng.

Số tiền Nam phải trả để mua truyện tranh là 15 000.(x + 5) đồng.

b) Tổng số tiền Nam phải trả để mua số sách là:

21 500x + 12 500(x + 8) + 15 000(x + 5)

= 21 500x + 12 500x + 12 500.8 + 15 000x + 15 000.5

= (21 500x + 12 500x + 15 000x) + 100 000 + 75 000

= 49 000x + 175 000 đồng.

Vậy đa thức biểu thị tổng số tiền Nam phải trả là 49 000x + 175 000.

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Bài 7.17 trang 33 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến

Bài 7.17 trang 33 Toán 7 Tập 2: Trên một mảnh đất hình chữ nhật có chiều dài 65 m, người ta định làm một bể bơi có chiều rộng là x mét, chiều dài gấp 3 lần chiều rộng. Sơ đồ và kích thước cụ thể (tính bằng mét) được cho trong Hình 7.1 Tìm đa thức (biến x):

a) Biểu thị diện tích của bể bơi.

b) Biểu thị diện tích mảnh đất.

c) Biểu thị diện tích phần đất xung quanh bể bơi.

Lời giải:

a) Do chiều dài của bể bơi gấp 3 lần chiều rộng nên chiều dài của bể bơi là 3x m.

Diện tích của bể bơi là 3x.x = 3x² (m²).

b) Chiều rộng của mảnh đất là: 4 + x + 5 = x + 9 (m).

Diện tích mảnh đất là: 65(x + 9) (m²).

c) Diện tích phần đất xung quanh bể bơi bằng diện tích mảnh đất trừ đi diện tích bể bơi.

Diện tích phần đất xung quanh bể bơi bằng:

65(x + 9) - 3x² = 65x + 65.9 - 3x² = -3x² + 65x + 585 (m²).

Lời giải bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến hay, chi tiết khác:

Sách bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến - Kết nối tri thức

Với giải sách bài tập Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 26.

Giải SBT Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến - Kết nối tri thức

Giải SBT Toán 7 trang 28 Tập 2

Vở thực hành Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến - Kết nối tri thức

Với giải vở thực hành Toán lớp 7 Bài 26: Phép cộng và phép trừ đa thức một biến sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài 26.

Giải vở thực hành Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến - Kết nối tri thức

Giải VTH Toán 7 trang 33 Tập 2

Phép cộng và phép trừ đa thức một biến (Lý thuyết Toán lớp 7) - Kết nối tri thức

Với tóm tắt lý thuyết Toán 7 Bài 26: Phép cộng và phép trừ đa thức một biến sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Phép cộng và phép trừ đa thức một biến (Lý thuyết Toán lớp 7) - Kết nối tri thức

Lý thuyết Phép cộng và phép trừ đa thức một biến

1. Cộng hai đa thức một biến

• Cách 1: Viết hai đa thức trong dấu ngoặc rồi nối chúng bởi dấu “+”. Sau đó bỏ ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.

• Cách 2: Đặt tính cộng sao cho các hạng tử cùng bậc của hai đa thức thì thẳng cột với nhau rồi cộng theo từng cột. Nếu đa thức khuyết một hạng tử bậc nào đó thì ta để một khoảng trống ứng với hạng tử đó.

Ví dụ:

+ Cho hai đa thức A(x) = x⁴ + 2x³ – x² + 9x – 3; B(x) = – x⁴ + 5x² – 3x + 1

Muốn tính tổng hai đa thức A(x) và B(x) ta làm như sau:

Cách 1:

A(x) + B(x)

= (x⁴ + 2x³ – x² + 9x – 3) + (– x⁴ + 5x² – 3x + 1) ⟵ Viết hai đa thức trong dấu ngoặc

= x⁴ + 2x³ – x² + 9x – 3 – x⁴ + 5x² – 3x + 1 ⟵ Bỏ dấu ngoặc

= (x⁴ – x⁴) + 2x³ + (– x² + 5x²) + (9x – 3x) – (3 – 1) ⟵ Nhóm các hạng tử cùng bậc

= 2x³ + 4x² + 6x – 2

Vậy A(x) + B(x) = 2x³ + 4x² + 6x – 2.

Cách 2: Đặt tính. Ta thấy đa thức B(x) bị khuyết hạng tử bậc 3 nên ta để khoảng trống ứng với hạng tử này khi đặt tính.

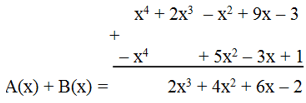
Chú ý: Phép cộng đa thức cũng có tính chất như phép cộng số thực. Cụ thể là:

+ Tính chất giao hoán: A + B = B + A;

+ Tính chất kết hợp: (A + B) + C = A + (B + C);

+ Cộng với đa thức không: A + 0 = 0 + A = A.

2. Trừ hai đa thức một biến

• Cách 1: Viết hai đa thức trong dấu ngoặc rồi nối chúng bởi dấu “–”. Sau đó bỏ ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.

• Cách 2: Đặt tính trừ sao cho các hạng tử cùng bậc của hai đa thức thì thẳng cột với nhau rồi trừ theo từng cột. Nếu đa thức khuyết một hạng tử bậc nào đó thì ta để một khoảng trống ứng với hạng tử đó.

Ví dụ:

+ Cho hai đa thức A(x) = x⁴ + 2x³ – x² + 9x – 3; B(x) = – x⁴ + 5x² – 3x + 1

Muốn tính hiệu A(x) – B(x) ta làm như sau:

Cách 1:

A(x) – B(x)

= (x⁴ + 2x³ – x² + 9x – 3) – (– x⁴ + 5x² – 3x + 1) ⟵ Viết hai đa thức trong dấu ngoặc

= x⁴ + 2x³ – x² + 9x – 3 + x⁴ – 5x² + 3x – 1 ⟵ Bỏ dấu ngoặc

= (x⁴ + x⁴) + 2x³ – (x² + 5x²) + (9x + 3x) – (3 + 1) ⟵ Nhóm các hạng tử cùng bậc

= 2x⁴ + 2x³ – 6x² + 12x – 4

Vậy A(x) – B(x) = 2x⁴ + 2x³ – 6x² + 12x – 4.

Cách 2:

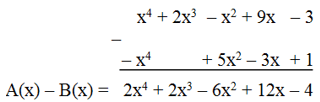
Chú ý: Tương tự như các số, với các đa thức P, Q và R, ta cũng có:

- Nếu Q + R = P thì R = P – Q.

- Nếu R = P – Q thì Q + R = P.

Bài tập Phép cộng và phép trừ đa thức một biến

Bài 1. Cho 3 đa thức:

A(x) = x⁴ + 2x³ + 2x² – x – 2;

B(x) = 3x⁴ – x³ + x² – 2x + 1;

C(x) = – 3x⁴ + x³ – 2x + 1;

a) Tính A(x) + B(x);

b) Tính A(x) – B(x);

c) Tính A(x) + B(x) + C(x);

d) Tính C(x) – B(x) – A(x).

Hướng dẫn giải

a) Cách 1:

A(x) + B(x) = (x⁴ + 2x³ + 2x² – x – 2) + (3x⁴ – x³ + x² – 2x + 1)

= x⁴ + 2x³ + 2x² – x – 2 + 3x⁴ – x³ + x² – 2x + 1

= (x⁴ + 3x⁴) + (2x³ – x³) + (2x² + x²) – (x + 2x) – (2 – 1)

= 4x⁴ + x³ + 3x² – 3x – 1

Cách 2: Đặt tính

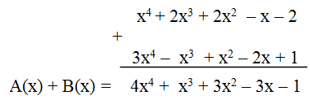
b) Cách 1:

A(x) – B(x) = (x⁴ + 2x³ + 2x² – x – 2) – (3x⁴ – x³ + x² – 2x + 1)

= x⁴ + 2x³ + 2x² – x – 2 – 3x⁴ + x³ – x² + 2x – 1

= (x⁴ – 3x⁴) + (2x³ + x³) + (2x² – x²) + (– x + 2x) – (2 + 1)

= – 2x⁴ + 3x³ + x² + x – 3

Cách 2: Đặt tính

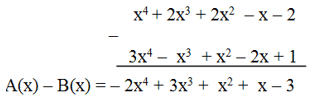
c) Đặt tính:

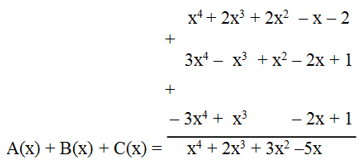
Vậy A(x) + B(x) + C(x) = x⁴ + 2x³ + 3x² – 5x.

d) Đặt tính

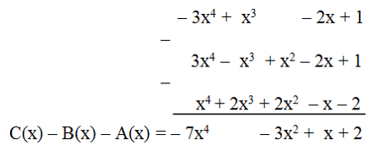
Vậy C(x) – B(x) – A(x) = – 7x⁴ – 3x² + x + 2.

Bài 2. Cho P(x) = 2x⁴ – x² + x – 2; Q(x) = 3x⁴ + x³ + 2x² + x + 1.

a) Tìm đa thức H(x), biết H(x) + P(x) = Q(x);

b) Tìm đa thức M(x), biết M(x) – Q(x) = P(x).

Hướng dẫn giải

a) H(x) + P(x) = Q(x)

nên H(x) = Q(x) – P(x)

= (3x⁴ + x³ + 2x² + x + 1) – (2x⁴ – x² + x – 2)

= 3x⁴ + x³ + 2x² + x + 1 – 2x⁴ + x² – x + 2

= (3x⁴ – 2x⁴) + x³ + (2x² + x²) + (x – x) + (1 + 2)

= x⁴ + x³ + 3x² + 3

Vậy H(x) = x⁴ + x³ + 3x² + 3.

b) M(x) – Q(x) = P(x)

nên M(x) = Q(x) + P(x)

= (3x⁴ + x³ + 2x² + x + 1) + (2x⁴ – x² + x – 2)

= 3x⁴ + x³ + 2x² + x + 1 + 2x⁴ – x² + x – 2

= (3x⁴ + 2x⁴) + x³ + (2x² – x²) + (x + x) + (1 – 2)

= 5x⁴ + x³ + x² + 2x – 1

Vậy M(x) = 5x⁴ + x³ + x² + 2x – 1.

Bài 3. Một xe khách đi từ Hà Nội đến Hải Phòng với vận tốc 60 km/h. Sau đó 30 phút, một xe du lịch cũng đi từ Hà Nội đến Hải Phòng với vận tốc 80km/h. Cả hai xe đều không nghỉ dọc đường.

a) Gọi A(x) là đa thức biểu thị quãng đường xe du lịch đi được và B(x) là đa thức biểu thị quãng đường xe khách đi được kể từ khi xuất phát đến khi xe du lịch đi được x giờ. Tìm A(x) và B(x).

b) Chứng tỏ rằng đa thức G(x) = A(x) – B(x) có nghiệm là x = $\frac{3}{2}$. Hãy giải thích ý nghĩa nghiệm $\frac{3}{2}$ của đa thức G(x).

Hướng dẫn giải

a) Quãng đường xe du lịch đi được sau x giờ là: 80x (km)

Khi xe du lịch đi được x giờ thì xe khách đi được khoảng thời gian là:

x giờ + 30 phút = x + 0,5 (giờ)

Quãng đường xe khách đi được sau khi xe du lịch đi được x giờ là:

60 . (x + 0,5) = 60x + 30 (km)

Vậy A(x) = 80x; B(x) = 60x + 30.

b) G(x) = A(x) – B(x)

= 80x – (60x + 30)

= 80x – 60x – 30

= 20x – 30

Vậy G(x) = 20x – 30.

Ta có: $G\left(\frac{3}{2}\right)=20\cdot \frac{3}{2}-30=0$

Vậy x = $\frac{3}{2}$ là nghiệm của đa thức G(x).

Nghiệm x = $\frac{3}{2}$ cho thấy sau $\frac{3}{2}$ giờ thì quãng đường đi được của xe khách bằng xe du lịch hay sau 1,5 giờ thì hai xe gặp nhau.

Học tốt Phép cộng và phép trừ đa thức một biến

Các bài học để học tốt Phép cộng và phép trừ đa thức một biến Toán lớp 7 hay khác:

15 Bài tập Phép cộng và phép trừ đa thức một biến (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Phép cộng và phép trừ đa thức một biến Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Phép cộng và phép trừ đa thức một biến (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Xem thử

Chỉ 150k mua trọn bộ trắc nghiệm Toán 7 Kết nối tri thức (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: