Với giải bài tập Toán 8 Bài tập cuối chương 7 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 Bài tập cuối chương 7.

Giải Toán 8 Chân trời sáng tạo Bài tập cuối chương 7

Video Giải Toán 8 Bài tập cuối chương 7 - Cô Vương Hiên (Giáo viên VietJack)

Giải Toán 8 trang 58

Câu hỏi trắc nghiệm

Bài 1 trang 58 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 1 trang 58 Toán 8 Tập 2: Cho tam giác ABC, biết DE // BC và AE = 6 cm, EC = 3 cm, DB = 2 cm (Hình 1). Độ dài đoạn thẳng AD là

A. 4 cm

B. 3 cm

C. 5 cm

D. 3.5 cm

Lời giải:

Đáp án đúng là: A

Xét tam giác ABC có: DE // BC

Theo định lí Thalès ta có: 

$\frac{AD}{DB}=\frac{AE}{EC}\Rightarrow \frac{x}{2}=\frac{6}{3}\Rightarrow x=4$(cm)

Vậy x = 4 (cm).

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 2 trang 58 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 2 trang 58 Toán 8 Tập 2: Cho tam giác ABC, biết DE // BC (Hình 2). Trong các khẳng định sau, khẳng định nào sai?

A. $\frac{AD}{DB}=\frac{AE}{EC}$ .

B. $\frac{AD}{AB}=\frac{AE}{AC}$ .

C. $\frac{AE}{AC}=\frac{DE}{BC}$ .

D. $\frac{DB}{AB}=\frac{DE}{BC}$ .

Lời giải:

Đáp án đúng là: D

Xét tam giác ABC có DE // BC.

Theo định lí Thalès, ta có:

$\frac{AD}{DB}=\frac{AE}{EC}; \frac{AD}{AB}=\frac{AE}{AC}; \frac{AE}{AC}=\frac{DE}{BC}; \frac{AD}{AB}=\frac{DE}{BC}$.

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 3 trang 58 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 3 trang 58 Toán 8 Tập 2: Cho Hình 3, biết AM = 3 cm, MN = 4 cm, AC = 9 cm. Giá trị của biểu thức x – y là:

A. 4.

B. – 3.

C. 3.

D. – 4.

Lời giải:

Đáp án đúng là: B

Xét tam giác AMN vuông tại M, theo định lí Pythagore, ta có:

$AN=\sqrt{A{M}^2+M{N}^2}=\sqrt{3^2+4^2}=5$

Theo hệ quả định lí Thalès, ta có: 

$\frac{AN}{AC}=\frac{AN}{AB}=\frac{MM}{BC}$.

Suy ra $\frac{3}{9}=\frac{5}{y}=\frac{4}{x}$, vậy x = 12, y = 15.

Do đó, x – y = 12 – 15 = – 3.

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 4 trang 58 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 4 trang 58 Toán 8 Tập 2: Cho tam giác MNP có MD là tia phân giác của góc M (D ∈ NP). Trong các khẳng định sau, khẳng định nào đúng?

A. $\frac{DN}{MN}=\frac{DP}{MP}$ .

B. $\frac{DN}{MN}=\frac{MP}{DP}$ .

C. $\frac{DN}{MN}=\frac{MP}{DP}$ .

D. $\frac{MN}{MP}=\frac{DP}{DN}$ .

Lời giải:

Đáp án đúng là: A

Xét tam giác MNP có MD là tia phân giác của góc M (D ∈ NP), ta có:

$\frac{DP}{DN}=\frac{MP}{MN}\Rightarrow \frac{DN}{MN}=\frac{DP}{MP}$

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 5 trang 58 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 5 trang 58 Toán 8 Tập 2: Cho hai đoạn thẳng AB = 12 cm và CD = 18 cm. Tỉ số của hai đoạn thẳng AB và CD là

A. $\frac{4}{3}$ .

B. $\frac{3}{4}$ .

C. $\frac{2}{3}$ .

D. $\frac{3}{2}$ .

Lời giải:

Đáp án đúng là: C

Tỉ số của hai đoạn thẳng AB và CD là: $\frac{AB}{CD}=\frac{12}{18}=\frac{2}{3}$

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 6 trang 58 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 6 trang 58 Toán 8 Tập 2: Cho Hình 4, biết MN // BC, AN = 4 cm. NC = 8 cm, MN = 5 cm. Độ dài cạnh BC là

A. 10 cm.

B. 20 cm.

C. 15 cm.

D. 16 cm.

Lời giải:

Đáp án đúng là: C

Xét tam giác ABC có MN // BC.

Theo hệ quả định lí Thalès, ta có:

$\frac{AN}{AC}=\frac{MN}{BC}\Rightarrow \frac{4}{4+8}=\frac{5}{BC}\Rightarrow BC=15\left(cm\right)$.

Vậy BC = 15 cm.

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 7 trang 59 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 7 trang 59 Toán 8 Tập 2: Cho Hình 5, biết MN // DE, MN = 6 cm, MP = 3 cm, PE = 5 cm. Độ dài đoạn thẳng DE là

A. 6 cm

B. 5 cm

C. 8 cm

D. 10 cm

Lời giải:

Đáp án đúng là: D

Theo hệ quả định lí Thalès, ta có: 

$\frac{MP}{PE}=\frac{MN}{DE}\Rightarrow \frac{3}{5}=\frac{6}{DE}\Rightarrow DE=10\left(cm\right)$

Vậy DE = 10 cm.

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 8 trang 59 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 8 trang 59 Toán 8 Tập 2: Cho tam giác ABC, một đường thẳng song song với BC cắt AB và AC lần lượt tại D và E. Qua E kẻ đường thẳng song song với CD cắt AB tại F. Biết AB = 25 cm, AF = 9 cm, EF = 12 cm, độ dài đoạn DC là

A. 25 cm

B. 20 cm

C. 15 cm

D. 12 cm

Lời giải:

Đáp án đúng là: B

Xét tam giác ABC có: DE // BC.

Theo định lí Thalès, ta có: $\frac{AD}{AB}=\frac{AE}{AC}$

Tương tự, ta có: $\frac{AF}{AD}=\frac{AE}{AC}$

Do đó $\frac{AD}{AB}=\frac{AF}{AC}$.

Suy ra  $AD=\sqrt{AB.AF}=\sqrt{25.9}=15\left(cm\right)$

Xét tam giác ADC có EF // DC.

Theo hệ quả định lí Thalès, ta có: 

$\frac{A\mathrm{F}}{AD}=\frac{EF}{DC}$ $\Rightarrow \frac{9}{15}=\frac{12}{DC}\Rightarrow DC=2$

Vậy DC = 20 cm.

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 9 trang 59 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 9 trang 59 Toán 8 Tập 2: Cho tam giác ABC biết AM là đường phân giác. Trong các khẳng định sau, khẳng định nào đúng?

A. $\frac{BM}{MC}=\frac{AB}{AC}$ .

B. $\frac{AB}{MC}=\frac{BM}{AC}$ .

C. $\frac{AM}{MC}=\frac{AB}{AC}$ .

D. $\frac{BM}{MC}=\frac{AM}{AC}$ .

Lời giải:

Đáp án đúng là: A

Xét tam giác ABC có AM là đường phân giác, ta có: $\frac{BN}{MC}=\frac{AB}{AC}$ .

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 10 trang 59 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 10 trang 59 Toán 8 Tập 2: Cho tam giác ABC và điểm D trên cạnh AB sao cho AD = 13,5 cm, DB = 4,5 cm. Tính tỉ số các khoảng cách từ các điểm D và B đến cạnh AC.

Lời giải:

Gọi DH và BK lần lượt là khoảng cách từ D và B đến cạnh AC.

Ta có AB = AD + DB.

Khi đó AB = 13,5 + 4,5 = 18 (cm).

Vì DH // BK (cùng vuông góc với AC) nên áp dụng hệ quả định lí Thalès ta có:

$\frac{DH}{BK}=\frac{AD}{AB}=\frac{13,5}{18}=\frac{3}{4}$

Vậy tỉ số khoảng cách từ D và B đến cạnh AC là $\frac{3}{4}$

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 11 trang 59 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 11 trang 59 Toán 8 Tập 2: a) Độ cao AN và chiều dài bóng nắng của các đoạn thẳng AN, BN trên mặt đất được ghi lại như trong Hình 6. Tìm chiều cao AB của cái cây.

b) Một tòa nhà cao 24 m, đổ bóng nắng dài 36 m trên đường như Hình 7. Một người cao 1,6 m muốn đứng trong bóng râm của tòa nhà. Hỏi người đó có thể đứng cách tòa nhà xa nhất bao nhiêu mét?

Lời giải:

a) Ta có: $\frac{AB}{AN}=\frac{AC}{AM}\Rightarrow \frac{AB}{1,5}=\frac{2,4+2,9}{2,4}\Rightarrow AB=3,3125\left(m\right)$

Vậy AB = 3,3125 m.

b) 

Ta có: $\frac{AB}{DE}=\frac{BC}{DC}\Rightarrow \frac{24}{1,6}=\frac{36}{DC}$, do đó DC = 2,4 (m).

Mà BD + DC = BC suy ra BD = BC – DC hay x = 36 – 2,4 = 33,6 (m).

Vậy người đó có thể đứng cách tòa nhà xa nhất là 33,6 mét.

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 12 trang 59 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

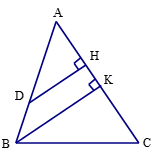
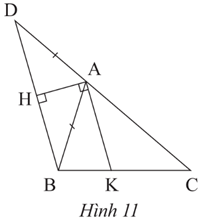
Bài 12 trang 59 Toán 8 Tập 2: Cho tam giác ABC có BC bằng 30 cm. Trên đường cao AH lấy các điểm K, I sao cho AK = KI = IH. Qua I và K vẽ các đường EF // BC, MN // BC (E, M ∈ AB; F, N ∈ AC).

a) Tính độ dài các đoạn thẳng MN và EF.

b) Tính diện tích tứ giác MNFE biết rằng diện tích tam giác ABC là 10,8 dm².

Lời giải:

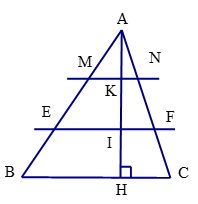
a) Vì MN // BC suy ra  $\frac{MN}{BC}=\frac{AM}{AB}$  (theo hệ quả định lí Thalès) (1)

Trong tam giác ABH có MK // BH suy ra $\frac{AK}{AH}=\frac{AM}{AB}$ (2)

Từ (1) và (2) suy ra $\frac{MN}{BC}=\frac{AK}{AH}$ .

Mà AK = KI = IH nên  $\frac{AK}{AH}=\frac{1}{3}$ suy ra $\frac{MN}{CB}=\frac{1}{3}$ .

Do đó $MN=\frac{1}{3}BC=\frac{1}{3}·30=10\left(\mathrm{cm}\right)$.

Tam giác ABC có EF // BC suy ra  $\frac{EF}{BC}=\frac{AI}{AH}=\frac{2}{3}$.

Do đó $\mathrm{EF}=\frac{2}{3}·30=20\left(\mathrm{cm}\right)$.

Tam giác ABC có EF // BC suy ra $\frac{EF}{BC}=\frac{AI}{AH}=\frac{2}{3}$ .

Do đó $EF=\frac{2}{3}.30=20$(cm) .

Vậy MN = 10 cm và EF = 20 cm.

b) Đổi 10,8 dm² = 1080 cm².

MN // BC mà AH ⊥ BC nên AK ⊥ MN hay AK là đường cao của tam giác AMN.

Ta có  $A\mathrm{K}=\frac{1}{3}A\mathrm{H}$.

$\frac{MN}{BC}=\frac{AK}{AH}=\frac{1}{3}\Rightarrow MN=\frac{1}{3}BC$.

Suy ra  $S_{AMN}=\frac{1}{2}AK.MN=\frac{1}{2}.\frac{1}{3}.AH.\frac{1}{3}BC=\frac{1}{9}\left(\frac{1}{2}AH.BC\right)$.

Hay $S_{AMN}=\frac{1}{9}{S}_{ABC}=120\left(c{m}^2\right)$ .

Tương tự, ta có: $S_{AEF}=\frac{4}{9}{S}_{ABC}=480\left(c{m}^2\right)$ .

Do đó $S_{MNEF}=S_{AEF}-S_{AMN}=480-120=360\left(c{m}^2\right)$ .

Vậy diện tích tứ giác MNFE là 360 cm².

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 13 trang 60 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 13 trang 60 Toán 8 Tập 2: Tính độ dài x trong Hình 8.

Lời giải:

a) Xét tam giác ABC có MN // BC, theo định lí Thalès, ta có: 

$\frac{AM}{MB}=\frac{AN}{NC}\Rightarrow \frac{2}{4}=\frac{x}{7}\Rightarrow x=\frac{7}{2}$.

Vậy  $x=\frac{7}{2}$.

b) Do CA ⊥ BD, DE ⊥ BD nên AC // DE.

Xét tam giác ABC có AC // DE.

Theo định lí Thalès, ta có: 

$\frac{AB}{BD}=\frac{BC}{BE}\Rightarrow \frac{3}{x}=\frac{5}{5+3,5}\Rightarrow x=5,1$.

Vậy x = 5,1.

c) Xét tam giác HIK có PQ // IK.

Theo định lí Thalès, ta có: 

$\frac{HP}{HI}=\frac{HQ}{HK}\Rightarrow \frac{x}{8}=\frac{6,5}{6,5+3,5}\Rightarrow x=5,2$.

Vậy x = 5,2.

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 14 trang 60 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 14 trang 60 Toán 8 Tập 2: Tính độ dài x trong Hình 9.

Lời giải:

a) Xét tam giác ABC có AD là tia phân giác góc A nên ta có:

$\frac{BC}{CD}=\frac{AB}{AC}\Rightarrow \frac{x}{5}=\frac{4,5}{7,2}\Rightarrow x=\frac{5.4,5}{7,2}=3,125$.

Vậy x = 3,125.

b) Xét tam giác MNP có MI là phân giác góc M nên ta có: 

$\frac{IN}{IP}=\frac{MN}{MP}\Rightarrow \frac{3}{x-3}=\frac{5}{8,5}\Rightarrow x-3=\frac{3.8,5}{5}=5,1$.

Do đó x = 8,1.

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 15 trang 60 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 15 trang 60 Toán 8 Tập 2: Cho tứ giác ABCD có AC và BD cắt nhau tại O. Qua O, kẻ đường thẳng song song với BC cắt AB tại E, kẻ đường thẳng song song với CD cắt AD tại F.

a) Chứng minh FE // BD;

b) Từ O kẻ đường thẳng song song với AB cắt BC tại G và đường thẳng song song với AD cắt CD tại H. Chứng minh rằng CG.DH = BG.CH.

Lời giải:

a) Tam giác ABC có OE // BC (gt)

Suy ra  $\frac{A\mathrm{E}}{AB}=\frac{AO}{AC}$ (theo định lí Thalès) (1)

Tam giác ADC có OF // CD (gt)

Suy ra  $\frac{AO}{AC}=\frac{A\mathrm{F}}{AD}$ (theo định lí Thalès) (2)

Từ (1) và (2) suy ra $\frac{AE}{AC}=\frac{AF}{AD}$

Tam giác ADB có  $\frac{AE}{AC}=\frac{AF}{AD}$

Suy ra EF // BD (theo định lí Thalès đảo)

b) Tam giác ABC có OG // AB (gt)

Suy ra $\frac{CG}{BG}=\frac{CO}{AO}$ (theo định lí Thalès) (3)

Tam giác ACD có OH // AD (gt)

Suy ra  $\frac{CO}{AO}=\frac{C\mathrm{H}}{DH}$ (theo định lí Thalès) (4)

Từ (3) (4) suy ra  $\frac{CG}{BG}=\frac{CH}{DH}$ ⇒ CG.DH = BG.CH

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 16 trang 60 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 16 trang 60 Toán 8 Tập 2: Cho hình bình hành ABCD. Đường thẳng a đi qua A cắt BD, BC, DC lần ượt tại E, K, G (Hình 10). Chứng minh rằng:

a) AE² = EK.EG.

b)  $\frac{1}{AE}=\frac{1}{AK}+\frac{1}{AG}$ .

Lời giải:

a) Vì ABCD là hình bình hành nên :

• AD // BC hay AD // BK

• AB // CD hay AB // DG

Áp dụng định lí Thalès ta có:

• AD // BK suy ra  $\frac{AE}{EK}=\frac{ED}{EB}$ (1)

• AB // DG suy ra  $\frac{ED}{EB}=\frac{EG}{AE}$  (2)

Từ (1) và (2) suy ra $\frac{AE}{EK}=\frac{EG}{AE}$ .

Do đó AE² = EK.EG (đpcm).

b) AB // DG suy ra $\frac{AE}{AG}=\frac{BE}{BD}$

AD // BC suy ra $\frac{AE}{AK}=\frac{DE}{BD}$

Suy ra  $\frac{AE}{AK}+\frac{AE}{AG}=\frac{DE}{BD}+\frac{BE}{BD}=\frac{BE+DE}{BD}=1$  (3)

Chia cả hai vế (3) cho AE ta được: $\frac{1}{A\mathrm{K}}+\frac{1}{AG}=\frac{1}{AE}$  (đpcm).

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác:

Bài 17 trang 60 Toán 8 Tập 2 Chân trời sáng tạo

Giải Toán 8 Bài tập cuối chương 7 - Chân trời sáng tạo

Bài 17 trang 60 Toán 8 Tập 2: a) Quan sát Hình 11, chứng minh AK là đường phân giác của góc A trong tam giác ABC.

b) Dựa vào kết quả của câu a, hãy nêu cách vẽ đường phân giác của một góc trong tam giác bằng đường kẻ và êke.

Lời giải:

a) Xét tam giác ABH có $\widehat{AHB}=90°$

Suy ra  $\widehat{HAB}+\widehat{AHB}=90°$ (1)

Lại có: $\widehat{HAK}=90°$ suy ra  $\widehat{HAB}+\widehat{BAK}=90°$ (2)

Từ (1) và (2) suy ra  $\widehat{ABH}=\widehat{BAK}$ (3)

Mà hai góc này ở vị trí so le trong nên HB // AK.

Do đó  $\widehat{KAC}=\widehat{BDA}$ (hai góc đồng vị) (4)

Tam giác ABD có AD = AB.

Suy ra tam giác ABD cân tại A nên  $\widehat{BDA}=\widehat{ABH}$ (5)

Từ (3), (4), (5) suy ra  $\widehat{BAK}=\widehat{KAC}$.

Vậy AK là phân giác góc  $\widehat{BAC}$.

b)

Giả sử để vẽ tia phân giác giác của góc xOy ta làm như sau:

- Ox' là tia đối của tia Ox.

- Trên Ox' và Oy lần lượt lấy H và K sao cho OH = OK, nối H với K.

- Từ O kẻ tia Oz song song với HK.

- Ta được Oz là tia phân giác góc xOy.

Lời giải bài tập Toán 8 Bài tập cuối chương 7 hay, chi tiết khác: