Tổng và hiệu hai lập phương (Lý thuyết Toán lớp 8) | Kết nối tri thức
Với tóm tắt lý thuyết Toán 8 Bài 8: Tổng và hiệu hai lập phương sách Kết nối tri thức hay nhất, chi tiết
sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.
Tổng và hiệu hai lập phương (Lý thuyết Toán lớp 8) | Kết nối tri thức
Lý thuyết Tổng và hiệu hai lập phương
1. Tổng hai lập phương
+ Với hai số a, b bất kì ta thức hiện phép tính:
(a + b).(a2 – ab + b2) = a3 – a2b + ab2 + a2b – ab2 + b3 = a3 + b3
Vậy (a + b).(a2 – ab + b2) = a3 + b3.
+ Với A, B là hai biểu thức bất kì, ta có:
A3 + B3 = (A + B)(A2 – AB + B2).
Ví dụ 1: Viết các đa thức sau dưới dạng tích:
a) x3 + 1;
b) x3 + 8y3.
Hướng dẫn giải
a) x3 + 1 = (x + 1)(x2 – x + 1);
b) x3 + 8y3 = x3 + (2y)3 = (x + 2y)(x2 – 2xy + 4y2).
Ví dụ 2: Rút gọn các biểu thức sau:
a) (2x + 1)(4x2 – 2x + 1) – 8x3;
b) (x + 4y)(x2 – 4xy + 16y2) – x3 – 65y3.
Hướng dẫn giải
a) (2x + 1)(4x2 – 2x + 1) – 8x3
= (2x)3 + 1 – 8x3
= 8x3 + 1 – 8x3
= 1.
b) (x + 4y)(x2 – 4xy + 16y2) – x3 – 65y3
= x3 + (4y)3 – x3 – 65y3
= x3 + 64y3 – x3 – 65y3
= –y3.
2. Hiệu hai lập phương
+ Với hai số a, b bất kì viết: a3 – b3 = a3 + (–b)3, sử dụng hằng đẳng thức tổng hai lập phương ta được: a3 – b3 = (a – b)(a2 + ab + b2).
+ Với A, B là hai biểu thức bất kì, ta có:
A3 – B3 = (A – B)(A2 + AB + B2).
Ví dụ 3: Viết các đa thức sau dưới dạng tích:
a) x3 – 27;
b) x3 – 8y3.
Hướng dẫn giải
a) x3 – 27 = x3 – 33 = (x – 3)(x2 + 3x + 9);
b) x3 – 8y3 = x3 – (2y)3 = (x – 2y)(x2 + 2xy + 4y2).
Ví dụ 4: Rút gọn biểu thức sau: (3x – 4)(9x2 + 12x + 16) – 27x3.
Hướng dẫn giải
(3x – 4)(9x2 + 12x + 16) – 27x3
= (3x)3 – 43 – 27x3
= 27x3 – 64 – 27x3
= –64.
CHÚ Ý: Các hằng đẳng thức vừa học được sử dụng thường xuyên trong các biến đổi đại số nên ta gọi chúng là các hằng đẳng thức đáng nhớ.
BẢY HẰNG ĐẲNG THỨC ĐÁNG NHỚ
|
A2 – B2 = (A + B)(A – B);
(A + B)2 = A2 + 2AB + B2;
(A – B)2 = A2 – 2AB + B2;
(A + B)3 = A3 + 3A2B + 3AB2 + B3;
(A – B)3 = A3 – 3A2B + 3AB2 – B3;
A3 + B3 = (A + B)(A2 – AB + B2);
A3 – B3 = (A – B)(A2 + AB + B2).
|
Bài tập Tổng và hiệu hai lập phương
Bài 1. Viết các biểu thức sau dưới dạng tổng hay hiệu hai lập phương:
a) (2x + 3y)(4x2 – 6xy + 9y2);
b) (5 – x)(25 + 5x + x2).
Hướng dẫn giải
a) (2x + 3y)(4x2 – 6xy + 9y2)
= (2x)3 + (3y)3
= 8x3 + 27y3;
b) (5 – x)(25 + 5x + x2)
= 53 – x3.
Bài 2. Thay ? bằng biểu thức thích hợp.
a) 27x3 + 343 = (3x + 7)(9x2 – ? + 49);
b) 729 – 8x3 = (? + 18x + 4x2)(? – 2x).
Hướng dẫn giải
a) 27x3 + 343 = (3x + 7)(9x2 – 21x + 49);
b) 729 – 8x3 = (81 + 18x + 4x2)(9 – 2x).
Bài 3. Rút gọn biểu thức sau:
(2x – 5)(4x2 + 10x + 25) + (2x + 5)(4x2 – 10x + 25).
Hướng dẫn giải
(2x – 5)(4x2 + 10x + 25) + (2x + 5)(4x2 – 10x + 25)
= 8x3 – 125 + 8x3 + 125
= 16x3.
Học tốt Tổng và hiệu hai lập phương
Các bài học để học tốt Tổng và hiệu hai lập phương Toán lớp 8 hay khác:
 bằng biểu thức thích hợp.
bằng biểu thức thích hợp. + 64);
+ 64); - 2y)(
- 2y)( + 64) ;
+ 64) ;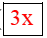 – 2y)[
– 2y)[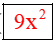 + 6xy + 4y2].
+ 6xy + 4y2].