Với giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 9 dễ dàng làm bài tập Toán 9 Bài 1.

Giải Toán 9 Cánh diều Bài 1: Căn bậc hai và căn bậc ba của số thực

Giải Toán 9 trang 48

Khởi động trang 48 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Khởi động trang 48 Toán 9 Tập 1: Một bàn cờ vua có dạng hình vuông gồm 64 ô vuông nhỏ (Hình 1).

Hỏi mỗi cạnh của bàn cờ gồm bao nhiêu cạnh ô vuông nhỏ?

Lời giải:

Mỗi cạnh của bàn cờ gồm 8 cạnh ô vuông nhỏ.

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Hoạt động 1 trang 48 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Hoạt động 1 trang 48 Toán 9 Tập 1: Tìm các số thực x sao cho:

a) x² = 9;

b) x² = 25.

Lời giải:

a) x² = 9

x² = 3² = (–3)²

x = 3 hoặc x = –3.

Vậy x ∈ {3; –3}.

b) x² = 25

x² = 5² = (–5)²

x = 5 hoặc x = –5

Vậy x ∈ {5; –5}.

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Luyện tập 1 trang 50 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Luyện tập 1 trang 50 Toán 9 Tập 1: Tìm căn bậc hai của 256; 0,04; $\frac{121}{36}$.

Lời giải:

Ta có:

⦁ 16² = (–16)² = 256 nên 16 và –16 là các căn bậc hai của 256.

⦁ (0,2)² = (–0,2)² = 0,04 nên 0,2 và –0,2 là các căn bậc hai của 0,04.

⦁ ${\left(\frac{11}{6}\right)}^2={\left(-\frac{11}{6}\right)}^2=\frac{121}{36}$ nên $\frac{11}{6}$ và -$\frac{11}{6}$ là các căn bậc hai của $\frac{121}{36}$.

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Hoạt động 2 trang 50 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Hoạt động 2 trang 50 Toán 9 Tập 1: Bạn Loan cần làm một chiếc hộp giấy có dạng hình lập phương với thể tích là 64 dm³. Hỏi cạnh của chiếc hộp giấy đó là bao nhiêu decimét? Biết rằng độ dày của tờ giấy để làm hộp là không đáng kể.

Lời giải:

Gọi a (dm) là độ dài cạnh của chiếc hộp giấy dạng hình lập phương đó (a > 0).

Khi đó, thể tích của chiếc hộp giấy đó là a³ (dm³).

Theo bài, ta có: a³ = 64 hay a³ = 4³, suy ra a = 4.

Vậy cạnh của chiếc hộp giấy đó là 4 decimét.

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Luyện tập 2 trang 51 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Luyện tập 2 trang 51 Toán 9 Tập 1: Tìm giá trị của:

a) $\sqrt[3]{-8};$

b) $\sqrt[3]{0,125};$

c) $\sqrt[3]{0}.$

Lời giải:

a) $\sqrt[3]{-8}$ = -2

b) $\sqrt[3]{0,125}$ = 0,5;

c) $\sqrt[3]{0}$ = 0.

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Hoạt động 3 trang 51 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Hoạt động 3 trang 51 Toán 9 Tập 1: Ta có thể tính được giá trị (đúng hoặc gần đúng) căn bậc hai, căn bậc ba của một số hữu tỉ bằng máy tính cầm tay.

⦁ Để tính căn bậc hai của một số hữu tỉ dương, ta sử dụng phím

⦁ Để tính căn bậc ba của một số hữu tỉ, ta sử dụng liên tiếp hai phím

Chẳng hạn, để tính $\sqrt{5},-\sqrt{11},\sqrt[3]{343},\sqrt[3]{-215},$ ta làm như sau:

Lời giải:

Học sinh làm theo hướng dẫn của giáo viên và sách giáo khoa.

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Luyện tập 3 trang 52 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Luyện tập 3 trang 52 Toán 9 Tập 1: Sử dụng máy tính cầm tay để tính giá trị (đúng hoặc gần đúng) của:

a) $\sqrt{2,37};$

b) $\sqrt[3]{\frac{-7}{11}}.$

Lời giải:

Để tính $\sqrt{2,37}$ và $\sqrt[3]{\frac{-7}{11}},$ ta làm như sau:

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Bài 1 trang 53 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Bài 1 trang 53 Toán 9 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Mỗi số dương có đúng hai căn bậc hai là hai số đối nhau.

b) Số âm không có căn bậc hai.

c) Số âm không có căn bậc ba.

d) Căn bậc ba của một số dương là số dương.

e) Căn bậc ba của một số âm là số âm.

Lời giải:

Phát biểu đúng là: a; b; d; e.

Phát biểu sai là: c. Vì mỗi số thực đều có duy nhất một căn bậc ba nên số âm cũng có căn bậc ba.

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Bài 2 trang 53 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Bài 2 trang 53 Toán 9 Tập 1: Tìm căn bậc hai của:

a) 289;

b) 0,81;

c) 1,69;

d) $\frac{49}{121}.$

Lời giải:

a) Do 17² = (–17)² = 289 nên 17 và –17 là các căn bậc hai của 289.

b) Do 9² = (–9)² = 81 nên 9 và –9 là các căn bậc hai của 81.

c) Do 1,3² = (–1,3)² = 1,69 nên 1,3 và –1,3 là các căn bậc hai của 1,69.

d) Do ${\left(\frac{7}{11}\right)}^2={\left(-\frac{7}{11}\right)}^2=\frac{49}{121}$ nên $\frac{7}{11}$ và -$\frac{7}{11}$ là các căn bậc hai của $\frac{49}{121}.$

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Bài 3 trang 53 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Bài 3 trang 53 Toán 9 Tập 1: Tìm căn bậc ba của:

a) 1 331;

b) –27;

c) –0,216;

d) $\frac{8}{343}.$

Lời giải:

a) Ta có 11³ = 1 331 nên $\sqrt[3]{1331}$ = 11.

b) Ta có (–3)³ = –27 nên $\sqrt[3]{-27}$ = -3.

c) Ta có (–0,6)³ = –0,216 nên $\sqrt[3]{-0,216}$ = -0,6.

d) Ta có ${\left(\frac{2}{7}\right)}^3=\frac{8}{343}$ nên $\sqrt[3]{\frac{8}{343}}=\frac{2}{7}.$

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Bài 4 trang 54 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Bài 4 trang 54 Toán 9 Tập 1: So sánh:

a) $\sqrt{\frac{4}{3}}$ và $\sqrt{\frac{3}{4}}$;

b) $\sqrt{0,48}$ và 0,7;

c) $\sqrt{-45}$ và $\sqrt{-50}$;

d) –10 và $\sqrt{-999}$.

Lời giải:

a)Ta có: $\frac{4}{3}>1>\frac{3}{4}$ nên $\frac{4}{3}>\frac{3}{4}$ do đó $\sqrt{\frac{4}{3}}>\sqrt{\frac{3}{4}}.$

b) Ta có: 0,7 = $\sqrt{0,49}$.

Do 0,48 < 0,49 nên $\sqrt{0,48}<\sqrt{0,49}$ hay $\sqrt{0,48}<\sqrt{0,7}.$

c) Ta có: –45 > – 50 nên $\sqrt[3]{-45}>\sqrt[3]{-50}.$

d) Ta có: -10 = $\sqrt[3]{-1000}.$

Do –1 000 < –999 nên $\sqrt[3]{-1000}<\sqrt[3]{-999}$ hay -10 < $\sqrt[3]{-999}$.

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Bài 5 trang 54 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Bài 5 trang 54 Toán 9 Tập 1: Chứng minh:

a) (2-$\sqrt{3}$)(2+$\sqrt{3}$) = 1;

b) ($\sqrt[3]{2}$+1)[($\sqrt[3]{2}$)² - $\sqrt[3]{2}$+1] = 3.

Lời giải:

a) Ta có: (2-$\sqrt{3}$)(2+$\sqrt{3}$) = 2²-($\sqrt{3}$)² = 4 - 3 = 1.

b) Ta có: ($\sqrt[3]{2}$+1)[($\sqrt[3]{2}$)²-$\sqrt[3]{2}$+1] = ($\sqrt[3]{2}$)³ + 1 = 2+1 = 3.

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Bài 6 trang 54 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

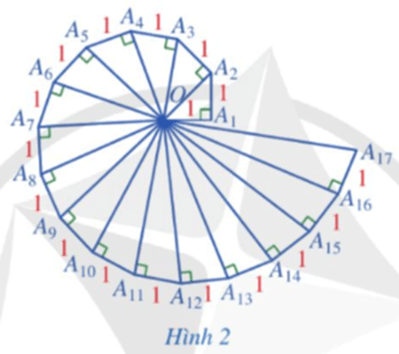
Bài 6 trang 54 Toán 9 Tập 1: Tính độ dài cạnh huyền của mỗi tam giác vuông trong Hình 2.

Lời giải:

Áp dụng định lí Pythagore cho:

⦁ ∆OA₁A₂ vuông tại A₁, ta có OA₂ = $\sqrt{O{A}_1^2+A_1{A}_2^2}=\sqrt{1^2+1^2}=\sqrt{2};$

⦁ ∆OA₂A₃ vuông tại A₂, ta có OA₃ =$\sqrt{O{A}_2^2+A_2{A}_3^2}=\sqrt{{\left(\sqrt{2}\right)}^2+1^2}=\sqrt{3};$

⦁ ∆OA₃A₄ vuông tại A₃, ta có OA₄ = $\sqrt{O{A}_3^2+A_3{A}_4^2}=\sqrt{{\left(\sqrt{3}\right)}^2+1^2}=\sqrt{4}=2;$

⦁ ∆OA₄A₅ vuông tại A₄, ta có OA₅ = $\sqrt{O{A}_4^2+A_4{A}_5^2}=\sqrt{2^2+1^2}=\sqrt{5};$

⦁ ∆OA₅A₆ vuông tại A₅, ta có OA₆ = $\sqrt{O{A}_5^2+A_5{A}_6^2}=\sqrt{{\left(\sqrt{5}\right)}^2+1^2}=\sqrt{6};$

Tương tự, ta cũng có: OA₇ = $\sqrt{7}$; $O{A}_8=\sqrt{8}=2\sqrt{2};$ $O{A}_9=\sqrt{9}=3;$$O{A}_{10}=\sqrt{10};$ $O{A}_{11}=\sqrt{11};$ $O{A}_{12}=\sqrt{12}=2\sqrt{3};$ $O{A}_{13}=\sqrt{13};$ $O{A}_{14}=\sqrt{14};$ $O{A}_{15}=\sqrt{15};$$O{A}_{16}=\sqrt{16}=4;$ $O{A}_{17}=\sqrt{17}.$

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Bài 7 trang 54 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Bài 7 trang 54 Toán 9 Tập 1: Đại Kim tự tháp Giza là Kim tự tháp Ai Cập lớn nhất và là lăng mộ của Vương triều thứ Tư của pharaoh Khufu. Nền kim tự tháp có dạng hình vuông với diện tích khoảng 53 052 m² (Nguồn: https://vi.wikipedia.org). Hỏi độ dài cạnh của nền kim tự tháp đó là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Lời giải:

Gọi a (m) là độ dài cạnh của nền kim tự tháp dạng hình vuông (a > 0).

Diện tích của nền kim tự tháp đó là a² (m²).

Theo bài, ta có: a² = 53 052, suy ra a = $\sqrt{53052}\approx$ 230,3 (m).

Vậy độ dài cạnh của nền kim tự tháp đó là khoảng 230,3 mét.

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Bài 8 trang 54 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

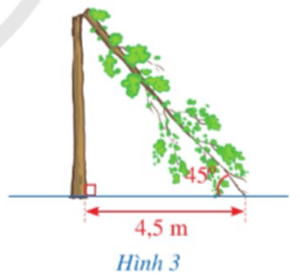
Bài 8 trang 54 Toán 9 Tập 1: Giông bão thổi mạnh, một cây bị gãy gập xuống làm ngọn cây chạm đất và tạo với phương nằm ngang một góc 45° (minh họa ở Hình 3). Người ta đo được khoảng cách từ chỗ ngọn cây chạm đất đến gốc cây là 4,5 m. Giả sử cây mọc vuông góc với mặt đất, hãy tính chiều cao của cây đó theo đơn vị mét (làm tròn kết quả đến hàng phần mười).

Lời giải:

Giả sử hình ảnh của cây được mô tả như hình vẽ dưới đây:

Vì ∆ABC vuông cân tại A có $\widehat{ACB}=45°$ nên ∆ABC vuông cân tại A.

Do đó AB = AC = 4,5 m.

Áp dụng định lí Pythagore vào ∆ABC vuông cân tại A, ta có:

BC² = AB² + AC²

Suy ra BC = $\sqrt{A{B}^2+A{C}^2}=\sqrt{4,5^2+4,5^2}=\sqrt{40,5}\approx$ 6,4 (m).

Vậy chiều cao của cây đó là khoảng 4,5 + 6,4 = 10,9 mét.

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác:

Bài 9 trang 54 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực - Cánh diều

Bài 9 trang 54 Toán 9 Tập 1: Thể tích của một khối bê tông có dạng hình lập phương là khoảng 220 348 cm³. Hỏi độ dài cạnh của khối bê tông đó là bao nhiêu cetimét (làm tròn kết quả đến hàng phần mười)?

Lời giải:

Gọi a (cm) là độ dài cạnh của khối bê tông dạng hình lập phương (a > 0).

Thể tích của khối bê tông đó là : a³ (cm³).

Theo bài, ta có: a³ = 220 348, suy ra a = $\sqrt[3]{220348}\approx$60,4 (cm).

Vậy độ dài cạnh của khối bê tông đó là khoảng 60,4 cetimét.

Lời giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực hay, chi tiết khác: