Bài 7 trang 45 Toán 10 Tập 2 Chân trời sáng tạo | Giải Toán 10

Giải Toán 10 Chân trời sáng tạo Bài 1: Toạ độ của vectơ

Bài 7 trang 45 Toán lớp 10 Tập 2: Cho tam giác ABC có các điểm M(2; 2), N(3; 4), P(5; 3) lần lượt là trung điểm của các cạnh AB, BC và CA.

a) Tìm tọa độ các đỉnh của tam giác ABC.

b) Chứng minh rằng trọng tâm của tam giác ABC và MNP trùng nhau.

c) Giải tam giác ABC.

Lời giải:

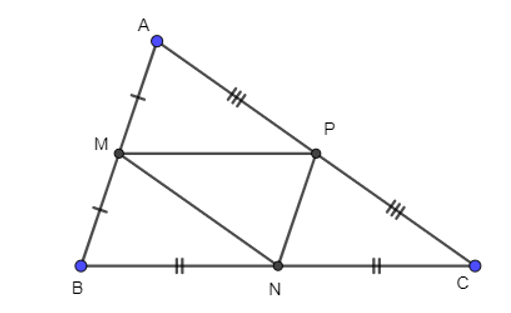
a) Gọi A(x_A; y_A), B(x_B; y_B), C(x_C; y_C).

Xét tam giác ABC, có:

M là trung điểm của AB

N là trung điểm của AC

Suy ra MN là đường trung bình của tam giác ABC

⇒ MN//AC hay MN //CP và MN // PA và MN = AP = PC = $\frac{1}{2}$AC

Ta có: $\overrightarrow{MN}\left(1;2\right)$, $\overrightarrow{PC}$(x_C – 5; y_C – 3)

Mà 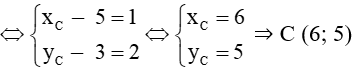$\overrightarrow{MN}=\overrightarrow{PC}$

Vì P là trung điểm của AC nên ta có tọa độ P thỏa mãn hệ phương trình:

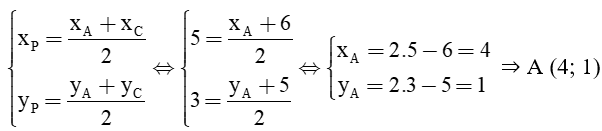
Vì M là trung điểm của AB nên ta có tọa độ M thỏa mãn hệ phương trình:

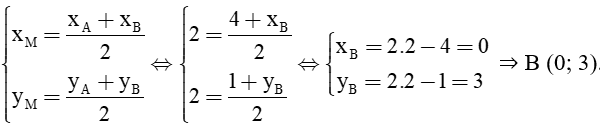
Vậy tọa độ các đỉnh của tam giác ABC lần lượt là: A(4; 1), B(0; 3) và C(6; 5).

b) Xét tam giác ABC, có A(4; 1), B(0; 3) và C(6; 5):

Gọi G là trọng tâm của tam giác ABC. Khi đó tọa độ trọng tâm của tam giác ABC là:

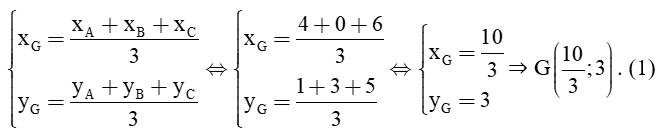
Xét tam giác MNP, có M(2; 2), N(3; 4), P(5; 3).

Gọi G là trọng tâm của tam giác MNP. Khi đó tọa độ trọng tâm của tam giác MNP là:

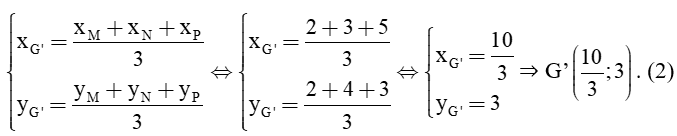
Từ (1) và (2) suy ra G và G’ trùng nhau.

Vậy tam giác ABC và tam giác MNP trùng trọng tâm.

c) Ta có: $\overrightarrow{AB}\left(-4;2\right)$ ⇒ AB = $\sqrt{{\left(-4\right)}^2+2^2}$ = $2\sqrt{5}$;

$\overrightarrow{AC}\left(2;4\right)$ ⇒ AC = $\sqrt{2^2+4^2}$ = $2\sqrt{5}$;

$\overrightarrow{BC}\left(6;2\right)$ ⇒ BC = $\sqrt{6^2+2^2}=2\sqrt{10}$.

Xét tam giác ABC:

Áp dụng hệ quả của định lí cosin, ta có:

cosA = $\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}=\frac{{\left(2\sqrt{5}\right)}^2+{\left(2\sqrt{5}\right)}^2-{\left(2\sqrt{10}\right)}^2}{2.\left(2\sqrt{5}\right).\left(2\sqrt{5}\right)}=0$

⇒ $\hat{A}=90°$.

Do AB = AC = $2\sqrt{5}$ nên ∆ABC vuông cân tại A

⇒ $\hat{B}=\hat{C}=45°$.

Vậy tam giác ABC, có AB = AC = $2\sqrt{5}$, BC = $2\sqrt{10}$, $\hat{A}=90°$ và $\hat{B}=\hat{C}=45°$.

Lời giải bài tập Toán 10 Bài 1: Toạ độ của vectơ hay, chi tiết khác: