Luyện tập 10 trang 57 Toán 12 Kết nối tri thức Tập 1

Giải Toán 12 Bài 6: Vectơ trong không gian - Kết nối tri thức

Luyện tập 10 trang 57 Toán 12 Tập 1: Trong Ví dụ 10, cho hình chóp tứ giác đều S.ABCD có độ dài tất cả các cạnh bằng a (H.2.26). Hãy tính các tích vô hướng $\overrightarrow{AS}\cdot \overrightarrow{BD}$ và $\overrightarrow{AS}\cdot \overrightarrow{CD}$.

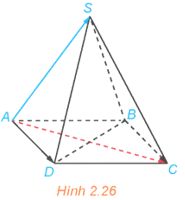
Lời giải:

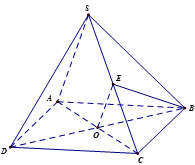
Gọi O là giao điểm của AC và BD.

Vì ABCD là hình vuông nên O là trung điểm của AC và BD.

Gọi E là trung điểm của SC. Suy ra OE là đường trung bình của tam giác SAC.

Suy ra $OE=\frac{SA}{2}=\frac{a}{2}$ và OE // SA.

Vì ABCD là hình vuông cạnh a nên $BD=a\sqrt{2}$  mà O là trung điểm của BD nên $OB=\frac{a\sqrt{2}}{2}$.

Vì ∆SBC đều cạnh a nên BE là đường cao. Suy ra $BE=\frac{a\sqrt{3}}{2}$ .

Vì $O{E}^2+O{B}^2={\left(\frac{a}{2}\right)}^2+{\left(\frac{a\sqrt{2}}{2}\right)}^2=\frac{3a^2}{4}=B{E}^2$ .

Do đó ∆BOE vuông tại O. Do đó $\overrightarrow{OE}\perp \overrightarrow{OB}$.

Vì OE // SA và $OE=\frac{1}{2}SA$ nên $\overrightarrow{AS}=2\overrightarrow{OE}$.

Vì O là trung điểm của BD nên $\overrightarrow{BD}=-2\overrightarrow{OB}$ .

Khi đó $\overrightarrow{AS}\cdot \overrightarrow{BD}=2\overrightarrow{OE}.\left(-2\overrightarrow{OB}\right)=0$.

Vì ABCD là hình vuông nên $\overrightarrow{CD}=\overrightarrow{BA}$.

Do đó $\overrightarrow{AS}\cdot \overrightarrow{CD}$ $=\overrightarrow{AS}\cdot \overrightarrow{BA}=-\overrightarrow{AS}\cdot \overrightarrow{AB}=-\left|\overrightarrow{AS}\right|\cdot \left|\overrightarrow{AB}\right|\cdot \cos \widehat{SAB}$.

Vì ∆SAB đều nên $\widehat{SAB}=60°$.

Do đó $\overrightarrow{AS}\cdot \overrightarrow{CD}=-a\cdot a\cdot \cos 60°=-\frac{a^2}{2}$.

Lời giải bài tập Toán 12 Bài 6: Vectơ trong không gian hay, chi tiết khác: