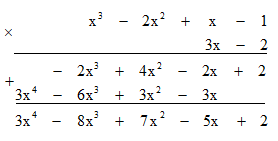Luyện tập 2 trang 38 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Luyện tập 2 trang 38 Toán 7 Tập 2: Tính (x³ - 2x² + x -1)(3x - 2). Trình bày lời giải theo hai cách

Lời giải:

Cách 1. Bỏ dấu ngoặc ta được:

(x³ - 2x² + x -1)(3x - 2)

= x³(3x - 2) + (-2x²).(3x - 2) + x.(3x - 2) + (-1)(3x - 2)

= x³.3x + x³.(-2) + (-2x²).3x + (-2x²).(-2) + x.3x + x.(-2) + (-1).3x + (-1).(-2)

= 3x⁴ + (-2x³) + (-6x³) + 4x² + 3x² + (-2x) + (-3x) + 2

= 3x⁴ + (-8x³) + 7x² + (-5x) + 2

= 3x⁴ - 8x³ + 7x² - 5x + 2

Vậy (x³ - 2x² + x -1)(3x - 2) = 3x⁴ - 8x³ + 7x² - 5x + 2.

Cách 2. Đặt phép tính ta được:

Vậy (x³ - 2x² + x -1)(3x - 2) = 3x⁴ - 8x³ + 7x² - 5x + 2.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác: