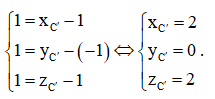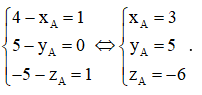Luyện tập 6 trang 71 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 2: Toạ độ của vectơ - Cánh diều

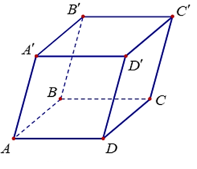
Luyện tập 6 trang 71 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có A'(1; 0; 1), B'(2; 1; 2), D'(1; – 1; 1), C(4; 5; – 5). Tìm tọa độ đỉnh A của hình hộp ABCD.A'B'C'D'.

Lời giải:

Ta có $\overrightarrow{A^{\text{'}}{B}^{\text{'}}}$ = (2 – 1; 1 – 0; 2 – 1) = (1; 1; 1).

Gọi tọa độ của điểm C' là (x_C'; y_C'; z_C'), ta có $\overrightarrow{D^{\text{'}}{C}^{\text{'}}}$ = (x_C' – 1; y_C' – (– 1); z_C' – 1).

Vì ABCD.A'B'C'D' là hình hộp nên A'B'C'D' là hình bình hành.

Do đó, $\overrightarrow{A^{\text{'}}{B}^{\text{'}}}=\overrightarrow{D^{\text{'}}{C}^{\text{'}}}$ . Suy ra

Khi đó, C'(2; 0; 2).

Ta có $\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$ = (2 – 1; 0 – 0; 2 – 1) = (1; 0; 1).

Gọi tọa độ của điểm A là (x_A; y_A; z_A), ta có $\overrightarrow{AC}=\left(4-x_A;5-y_A;-5-z_A\right)$ .

Vì ABCD.A'B'C'D' là hình hộp nên $\overrightarrow{AC}=\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$ .

Do đó,

Vậy A(3; 5; – 6).

Lời giải bài tập Toán 12 Bài 2: Toạ độ của vectơ hay, chi tiết khác: