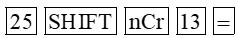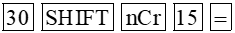Với giải bài tập Toán 10 Bài 3: Tổ hợp sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 10 dễ dàng làm bài tập Toán 10 Bài 3.

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Video Giải Toán 10 Bài 3: Tổ hợp - Cô Diệu Minh (Giáo viên VietJack)

Câu hỏi khởi động

Giải Toán 10 trang 15 Tập 2

Câu hỏi khởi động trang 15 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Câu hỏi khởi động trang 15 Toán lớp 10 Tập 2: Trong một giải bóng bàn đôi nam, mỗi đội 8 người chọn 2 vận động viên để tạo thành một cặp đấu.

Trong toán học, mỗi cách chọn 2 vận động viên từ 8 vận động viên để tạo thành một cặp đấu được gọi là gì?

Lời giải:

Sau bài học này, ta sẽ biết, mỗi cách chọn 2 vận động viên từ 8 vận động viên để tạo thành một cặp đấu được gọi là một tổ hợp chập 2 của 8.

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Hoạt động 1 trang 15 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Hoạt động 1 trang 15 Toán lớp 10 Tập 2: Đội tuyển bóng bàn nam của trường có 4 bạn Mạnh, Phong, Cường, Tiến. Huấn luyện viên muốn chọn 2 bạn để tạo thành một cặp đấu đôi nam.

a) Nêu 3 cách chọn cặp đấu.

b) Mỗi cặp đấu là một tập con gồm bao nhiêu phần tử được lấy ra từ tập hợp gồm 4 bạn nói trên?

Lời giải:

a) Ba cách chọn cặp đấu, chẳng hạn như sau:

Cách 1: Chọn 2 bạn Mạnh, Phong.

Cách 2: Chọn 2 bạn Cường, Tiến.

Cách 3: Chọn 2 bạn Phong, Tiến.

(Chọn 2 bạn bất kì trong 4 bạn).

b) Mỗi cặp đấu gồm 2 bạn trong 4 bạn của đội tuyển, do đó mỗi cặp đấu là một tập con gồm 2 phần tử được lấy ra từ tập hợp gồm 4 bạn nói trên.

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Luyện tập 1 trang 15 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Luyện tập 1 trang 15 Toán lớp 10 Tập 2: Viết tất cả tổ hợp chập 2 của 3 phần tử a, b, c.

Lời giải:

Mỗi tổ hợp chập 2 của 3 phần tử a, b, c là một tập con gồm 2 phần tử của tập A = {a; b; c}.

Vậy các tổ hợp chập 2 của 3 phần tử a, b, c là: {a; b}, {a; c}, {b; c}.

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Hoạt động 2 trang 15 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Hoạt động 2 trang 15 Toán lớp 10 Tập 2: Cho tập hợp A = {a; b; c; d; e}.

a) Nêu cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A.

b) Nêu cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A.

c) So sánh cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A với cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A.

Lời giải:

a) Cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A là trích ra một tập con gồm 3 phần tử lấy ra từ 5 phần tử trong A.

b) Cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A là lấy ra 3 phần tử từ 5 phần tử trong A và sắp xếp thứ tự 3 phần tử đó.

c) Việc lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A là lấy ra 3 phần tử trong 5 phần tử và sắp thứ tự, còn cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A là lấy ra 3 phần tử trong 5 phần tử và không sắp thứ tự.

Mỗi tổ hợp chập 3 của 5 phần tử sinh ra 3! chỉnh hợp chập 3 của 5 phần tử vì có 3! hoán vị của 3 phần tử. Vì thế, số chỉnh hợp chập 3 của 5 phần tử nhiều gấp 3! lần số tổ hợp chập 3 của 5 phần tử.

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Luyện tập 2 trang 17 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Luyện tập 2 trang 17 Toán lớp 10 Tập 2: Trong một buổi tập huấn cho các bí thư chi đoàn có 10 bạn nam. Hỏi có bao nhiêu cách chọn 3 bạn nam để tham gia một trò chơi?

Lời giải:

Mỗi cách chọn 3 bạn nam trong 10 bạn nam là một tổ hợp chập 3 của 10 phần tử.

Vậy số cách chọn 3 bạn nam để tham gia một trò chơi là $C_{10}^3$ = 120 (cách).

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Hoạt động 3 trang 17 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Hoạt động 3 trang 17 Toán lớp 10 Tập 2: Ta có thể tính số các tổ hợp bằng máy tính cầm tay như sau:

Lời giải:

Thực hiện bấm máy tính cầm tay theo hướng dẫn.

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Luyện tập 3 trang 17 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Luyện tập 3 trang 17 Toán lớp 10 Tập 2: Dùng máy tính cầm tay để tính:

a) $C_{25}^{13}$ ;

b) $C_{30}^{15}$.

Lời giải:

a) Ta mở máy tính cầm tay và thực hiện ấn các phím như sau:

Khi đó trên màn hình máy tính hiện kết quả: 5 200 300.

Vậy $C_{25}^{13}=5200300$

b) Ta mở máy tính cầm tay và thực hiện ấn các phím như sau:

Khi đó trên màn hình máy tính hiện kết quả: 155 117 520.

Vậy $C_{30}^{15}=155117520$

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Hoạt động 4 trang 17 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Hoạt động 4 trang 17 Toán lớp 10 Tập 2: So sánh:

a) $C_6^2$ và $C_6^4$;

b) $C_4^2+C_4^3$ và $C_5^3$ .

Lời giải:

a) Ta có: $C_6^2=\frac{6!}{2!\left(6-2\right)!}=\frac{6!}{2!.4!}=15$ ;

$C_6^4=\frac{6!}{4!\left(6-4\right)!}=\frac{6!}{4!.2!}=15$.

Do đó: $C_6^2=C_6^4$ .

b) Ta có: $C_4^2+C_4^3=\frac{4!}{2!\left(4-2\right)!}+\frac{4!}{3!\left(4-3\right)!}$ $=\frac{4!}{2!.2!}+\frac{4!}{3!.1!}=\frac{\mathrm{4.3.2.1}}{\mathrm{2.1.2.1}}+\frac{\mathrm{4.3.2.1}}{\mathrm{3.2.1}}$= 6 + 4 = 10;

$C_5^3=\frac{5!}{3!\left(5-3\right)!}=\frac{5!}{3!.2!}$$=\frac{\mathrm{5.4.3.2.1}}{\mathrm{3.2.1.2.1}}=10$.

Do đó: $C_4^2+C_4^3$ = $C_5^3$ .

Chú ý: Ta có thể sử dụng máy tính để tính rồi so sánh.

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Bài 1 trang 17 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Bài 1 trang 17 Toán lớp 10 Tập 2: Cho 8 điểm sao cho không có 3 điểm nào thẳng hàng. Có bao nhiêu tam giác với 3 đỉnh là 3 điểm trong 8 điểm đã cho?

Lời giải:

Chọn 3 điểm trong 8 điểm đã cho ta được 3 đỉnh của 1 tam giác.

Mỗi cách chọn 3 điểm trong 8 điểm là một tổ hợp chập 3 của 8, do đó có tam giác.

Vậy có 56 tam giác với 3 đỉnh là 3 điểm trong 8 điểm đã cho.

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Bài 2 trang 17 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Bài 2 trang 17 Toán lớp 10 Tập 2: Có 10 đội tham gia một giải bóng đá. Có bao nhiêu cách xếp trận đấu vòng tính điểm sao cho hai đội chỉ gặp nhau đúng một lần?

Lời giải:

Mỗi cách chọn 2 đội để đấu với nhau trong 10 đội tham gia giải bóng đá là một tổ hợp chập 2 của 10, do đó có $C_{10}^2=45$ cách xếp trận đấu vòng tính điểm sao cho hai đội chỉ gặp nhau đúng một lần.

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Bài 3 trang 17 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Bài 3 trang 17 Toán lớp 10 Tập 2: Khối 10 có 16 bạn nữ và 18 bạn nam tham gia đợt tình nguyện Mùa hè xanh. Đoàn trường dự định lập một tổ trồng cây gồm 3 học sinh có cả nam và nữ. Có bao nhiêu cách lập một tổ trồng cây như vậy?

Lời giải:

Khối đó có tổng cộng số học sinh tham gia tình nguyện là: 16 + 18 = 34 (học sinh).

Số cách lập một tổ trồng cây gồm 3 học sinh bất kì, có $C_{34}^3=5984$ (cách lập).

Số cách lập một tổ trồng cây gồm 3 học sinh toàn nữ là $C_{16}^3=560$ (cách lập).

Số cách lập một tổ trồng cây gồm 3 học sinh toàn nam là $C_{18}^3=816$ (cách lập).

Do đó, có 5 984 – 560 – 816 = 4 608 cách lập một tổ trồng cây gồm 3 học sinh có cả nam và nữ.

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Bài 4 trang 17 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Bài 4 trang 17 Toán lớp 10 Tập 2: Một quán nhỏ bày bán hoa có 50 bông hồng và 60 bông cúc. Bác Ngọc muốn mua 5 bông hoa gồm cả hai loại hoa trên. Bác Ngọc có bao nhiêu cách chọn hoa?

Lời giải:

Tổng số bông hoa của quán là: 50 + 60 = 110 (bông)

Số cách chọn 5 bông hoa bất kì trong 110 bông hoa là $C_{110}^5$ (cách chọn).

Số cách chọn 5 bông hoa hồng trong 50 bông hồng là $C_{50}^5$ (cách chọn).

Số cách chọn 5 bông hoa cúc trong 60 bông cúc là $C_{60}^5$ (cách chọn).

Do đó, có $C_{110}^5-C_{50}^5-C_{60}^5$ = 114 811 250 cách chọn 5 bông hoa gồm cả hai loại hoa.

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Bài 5 trang 17 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 3: Tổ hợp

Bài 5 trang 17 Toán lớp 10 Tập 2: Tính tổng $C_{15}^{12}+C_{15}^{13}+C_{16}^{14}$ .

Lời giải:

Cách 1: Ta có: $C_{15}^{12}+C_{15}^{13}+C_{16}^{14}$

$=C_{16-1}^{13-1}+C_{16-1}^{13}+C_{16}^{14}$$=C_{16}^{13}+C_{16}^{14}$

$=\frac{16!}{13!\left(16-13\right)!}+\frac{16!}{14!\left(16-14\right)!}$

$=\frac{\mathrm{16.15.14}}{\mathrm{3.2.1}}+\frac{16.15}{2.1}$

$=\mathrm{8.5.14}+8.15=560+120=680$

Cách 2: Sử dụng máy tính cầm tay.

$C_{15}^{12}+C_{15}^{13}+C_{16}^{14}$= 455 + 105 + 120 = 680.

Lời giải Toán 10 Bài 3: Tổ hợp hay, chi tiết khác:

Sách bài tập Toán 10 Bài 3: Tổ hợp - Cánh diều

Với giải sách bài tập Toán 10 Bài 3: Tổ hợp sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 Bài 3.

Sách bài tập Toán 10 Bài 3: Tổ hợp - Cánh diều

Giải SBT Toán 10 trang 13 Tập 2

Tổ hợp (Lý thuyết Toán lớp 10) - Cánh diều

Với tóm tắt lý thuyết Toán 10 Bài 3: Tổ hợp sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Tổ hợp (Lý thuyết Toán lớp 10) - Cánh diều

Lý thuyết Tổ hợp

1. Định nghĩa

Cho tập hợp A gồm n phần tử và một số nguyên k với 1 ≤ k ≤ n.

Mỗi tập con gồm k phần tử được lấy ra từ n phần tử của A được gọi là một tổ hợp chập k của n phần tử đó.

Ví dụ : Bạn Mai có 4 chiếc váy màu hồng, màu đỏ, màu trắng, màu tím. Mai muốn chọn 3 trong 4 chiếc váy để mang đi du lịch. Hãy viết các tổ hợp 3 của 4 chiếc áo váy đó.

Hướng dẫn giải

Các tổ hợp chập 3 của 4 chiếc váy là :

Hồng – đỏ – trắng ; Hồng – đỏ – tím ; Đỏ – trắng – tím ; Hồng – trắng – tím.

Vậy ta có 4 tổ hợp chập 3 của 4 chiếc váy là : Hồng – đỏ – trắng ; Hồng – đỏ – tím ; Đỏ – trắng – tím ; Hồng – trắng – tím.

2. Số các tổ hợp

Nhận xét : Một tổ hợp chập k của n phần tử nhiều gấp k! lần số tổ hợp chập k của n phần tử đó.

Kí hiệu là $C_n^k$ là số tổ hợp chập k của n phần tử với (1 ≤ k ≤ n). Ta có : $C_n^k=\frac{A_n^k}{k!}$

Quy ước 0! = 1 ; $C_n^0=1$.

Với những quy ước trên, ta có công thức sau: $C_n^k=\frac{n!}{(n-k)!k!}$ (với 0 ≤ k ≤ n).

Ví dụ : Một tổ có 8 người, bạn tổ trưởng muốn cử ra 4 bạn đi tập văn nghệ. Hỏi có bao nhiêu cách chọn ?

Hướng dẫn giải

Mỗi cách chọn 4 bạn trong 8 bạn đi trực nhật là một tổ hợp chập 4 của 8.

Ta có $C_8^4=\frac{8!}{(8-4)!4!}=70$.

Vậy có 70 cách chọn 4 trong 8 bạn đi tập văn nghệ.

3. Tính chất của các số $C_n^k$

Ta có hai đẳng thức sau : $C_n^k=C_n^{n-k}$ (0 ≤ k ≤ n) và $C_{n-1}^{k-1}+C_{n-1}^k=C_n^k$ (1 ≤ k < n).

Ví dụ: Ta có : $C_{10}^6=C_{10}^{10-6}=210$ ; $C_{10-1}^{6-1}+C_{10-1}^6=C_{10}^6=210$.

Bài tập Tổ hợp

Bài 1. Gia đình của Tú Mai muốn đi du lịch tại Ninh Bình. Hướng dẫn viên đưa ra một số địa điểm để du lịch như sau: Chùa Bái Đính; Hang Múa, quần thể danh thắng Tràng An, Vườn Quốc gia Cúc Phương, Tam Cốc – Bích Động; Cố đô Hoa Lư; Động Am Tiêm; Vườn Chim Thung Nham; Đầm Vân Long; Nhà thờ Phát Diệm. Biết rằng gia đình của Tú Mai chỉ đi được 4 trong số các địa điểm du lịch trên. Hỏi gia đình của Tú Mai có bao nhiêu cách để lựa chọn.

Hướng dẫn giải

Hướng dẫn viên đưa ra tất cả 10 địa điểm để gia đình của Tú Mai lựa chọn du lịch.

Gia đình của Tú Mai lựa chọn 4 trong 10 địa điểm du lịch.

Mỗi cách chọn đó là một tổ hợp chập 4 của 10 địa điểm du lịch.

Ta có: $C_{10}^4=\frac{10!}{(10-4)!4!}=210$.

Vậy gia đình Tú Mai có 210 cách để lựa chọn 4 trong 10 địa điểm để du lịch.

Bài 2 : Một túi có 7 quả bóng xanh, 3 quả bóng vàng và 14 quả bóng đỏ. Lấy ngẫu nhiên ba quả bóng trong túi. Hỏi có bao nhiêu cách để lấy 3 quả bóng từ trong túi sao cho 3 quả bóng cùng màu.

Hướng dẫn giải

Để lấy 3 quả bóng cùng màu thì ta thực hiện một trong ba hành động sau:

– Lấy 3 quả bóng màu xanh trong 7 quả bóng xanh, ta có $C_7^3$ = 35 cách lấy.

– Lấy 3 quả bóng màu vàng trong 3 quả bóng vàng, ta có $C_3^3$ = 1 cách lấy.

– Lấy 3 quả bóng màu đỏ trong 14 quả bóng đỏ, ta có $C_{14}^3$ = 364 cách lấy.

Theo quy tắc cộng, ta có 35 + 1 + 364 = 400 cách để lấy được 3 quả bóng cùng màu.

Vậy có 400 cách để lấy được 3 quả bóng cùng màu.

Bài 3: Bác Dũng có 8 người bạn. Bác Dũng muốn mời 4 trong 8 người bạn đó đi câu cá vào cuối tuần. Nhưng trong 8 người bạn đó, có 2 người bạn không thích câu cá nên không đi. Vậy số cách chọn nhóm 4 người để đi câu cùng bác Dũng là bao nhiêu?

Hướng dẫn giải

Bác Dũng có 8 người bạn nhưng có hai người không đi nên số người có thể đi câu cùng bác Dũng là 8 – 2 = 6 người.

Khi đó, bác Dũng chọn 4 người trong 6 người để đi câu cùng thì số cách chọn là tổ hợp chập 4 của 6 người bạn.

Ta có $C_6^4$= 15.

⇒ Bác Dũng có 15 cách để lựa chọn 4 người bạn trong 6 người bạn đi câu cá cùng.

Vậy bác Dũng có 15 cách để lựa chọn 4 người bạn đi câu cá cùng.

Bài 4: Tính $C_{30}^{19}+C_{30}^{20}-C_{31}^{20}$.

Hướng dẫn giải

Ta có $C_{30}^{19}+C_{30}^{20}=C_{31}^{20}$nên $C_{30}^{19}+C_{30}^{20}-C_{31}^{20}=C_{31}^{20}-C_{31}^{20}=0$.

Học tốt Tổ hợp

Các bài học để học tốt Tổ hợp Toán lớp 10 hay khác:

15 Bài tập Tổ hợp (có đáp án) - Cánh diều Trắc nghiệm Toán 10

Với 15 bài tập trắc nghiệm Tổ hợp Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.

15 Bài tập Tổ hợp (có đáp án) - Cánh diều Trắc nghiệm Toán 10

Câu 1.Tên 15 quả bóng khác nhau để vào trong hộp. Có bao nhiêu cách chọn ra 4 quả bóng.

A. 4!;

B. 15!;

C. 1 365;

D. 32 760.

Câu 2. Số tập con gồm ba phần tử khác nhau của một tập hợp gồm bảy phần tử khác nhau?

A. $\frac{7!}{3!}$;

B. $C_7^3$;

C. $A_7^3$;

D. 7.

Câu 3.Từ 6 điểm phân biệt thuộc đường thẳng ∆ và một điểm không thuộc đường thẳng ∆ ta có thể tạo được tất cả bao nhiêu tam giác?

A.210;

B.30;

C.15;

D.35;

Câu 4.Nếu $C_n^k=10$ và $A_n^k=60$. Thì k bằng

A. 3;

B. 5;

C. 6;

D. 10.

Câu 5. Có bao nhiêu giá trị nguyên dương của n thỏa mãn $A_n^2-3C_n^2=15-5n$

A. 0;

B. 1;

C. 2;

D. 3.

Câu 6. Số tam giác xác định bởi các đỉnh của một đa giác đều 10 cạnh là:

A. 35;

B. 120;

C. 240;

D. 720.

Câu 7. Đội văn nghệ của nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 4 học sinh từ đội văn nghệ để biễu diễn trong lễ bế giảng. Hỏi có bao nhiêu cách chọn sao cho có đúng hai học sinh lớp 12A được chọn?

A. 66;

B. 24;

C. 60;

D. 72.

Câu 8.Trong hộp có 5 quả cầu đỏ và 7 quả cầu xanh kích thước giống nhau. Lấy ngẫu nhiên 5 quả cầu từ hộp. Hỏi có bao nhiêu khả năng lấy được số quả cầu đỏ nhiều hơn số quả cầu xanh.

A. 245;

B. 3480;

C. 246;

D. 3360.

Câu 9.Một đa giác đều có số đường chéo gấp đôi số cạnh. Hỏi đa giác đó có bao nhiêu cạnh?

A. 5;

B. 6;

C. 7;

D. 8.

Câu 10. Cho k, n là các số nguyên dương, k ≤ n. Trong các phát biểu sau, phát biểu nào sai?

A. $A_n^k=n\left(n-1\right)\mathrm{...}\left(n-k+1\right)$;

B. P_n = n(n – 1)(n – 2)...2.1;

C. P_n = n!;

D. $A_n^k=\frac{n!}{k!}$.

Câu 11. Giá trị của n bằng bao nhiêu, biết $\frac{5}{C_5^n}-\frac{2}{C_6^n}=\frac{14}{C_7^n}$

A. n = 2 hoặc n = 4;

B. n = 5;

C. n = 4;

D. n = 3.

Câu 12. Cho đa giác đều n đỉnh, n $\in$ ℕ; n ≥ 3. Tìm giá trị của n biết rằng đa giác đã cho có 135 đường chéo.

A. 15;

B. 27;

C. 8;

D. 18.

Câu 13.Trong không gian cho 2n điểm phân biệt n $\in$ ℕ; n ≥ 3, trong đó không có 3 điểm nào thẳng hàng và trong 2n điểm đó có đúng n điểm cùng nằm trên mặt phẳng. Biết rằng có đúng 505 mặt phẳng phân biệt được tạo thành từ 2n điểm đã cho. Tìm n?

A.n = 9;

B.n = 7;

C. Không có n thỏa mãn;

D.n = 8.

Câu 14.Trong một giải cờ vua gồm nam và nữ vận động viên. Mỗi vận động viên phải chơi hai ván với mỗi động viên còn lại. Cho biết có 2 vận động viên nữ và cho biết số ván các vận động viên chơi nam chơi với nhau hơn số ván họ chơi với hai vận động viên nữ là 84. Hỏi số ván tất cả các vận động viên đã chơi?

A.168;

B.156;

C.132;

D.182.

Câu 15.Có 14 người gồm 8 nam và 6 nữ. Số cách chọn 6 người trong đó có đúng 2 nữ là

A.1078;

B. 1414;

C. 1050;

D. 1386.

Xem thêm bài tập trắc nghiệm Toán lớp 10 Cánh diều có đáp án hay khác: