Với giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 12 dễ dàng làm bài tập Toán 12 Bài 1.
Toán 12 Kết nối tri thức Bài 1: Tính đơn điệu và cực trị của hàm số
Giải Toán 12 | No tags
Mục lục
- Đang tải mục lục...
Mở đầu trang 5 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
Mở đầu trang 5 Toán 12 Tập 1: Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí s(t) (mét) của chất điểm trên trục số đã chọn tại thời điểm t (giây) được cho bởi công thức s(t) = t3 – 9t2 + 15t, t ≥ 0. Hỏi trong khoảng thời gian nào thì chất điểm chuyển động sang phải, trong khoảng thời gian nào thì chất điểm chuyển động sang trái?
Lời giải:
Ta có s(t) = t3 – 9t2 + 15t.
Có v(t) = s'(t) = 3t2 – 18t + 15.
Chất điểm chuyển động sang phải khi v(t) > 0.
Có v(t) > 0 và v(t) < 0 1 < t < 5.
Do t ≥ 0 nên ta có:
Chất điểm chuyển động sang phải khi t ∈ (0; 1) và (5; +∞).
Chất điểm chuyển động sang trái khi t ∈ (1; 5).
Vậy chất điểm chuyển động sang phải trong khoảng thời gian từ 0 giây đến 1 giây hoặc trong khoảng thời gian lớn hơn 5 giây, chất điểm chuyển động sang trái trong khoảng thời gian từ 1 giây đến 5 giây.
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
HĐ1 trang 6 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
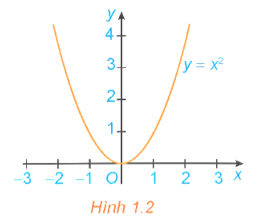
HĐ1 trang 6 Toán 12 Tập 1: Quan sát đồ thị của hàm số y = x2 (H.1.2)
a) Hàm số đồng biến trên khoảng nào?
b) Hàm số nghịch biến trên khoảng nào?
Lời giải:
a) Hàm số đồng biến trên khoảng (0; +∞).
b) Hàm số nghịch biến trên khoảng (−∞; 0).
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Luyện tập 1 trang 6 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
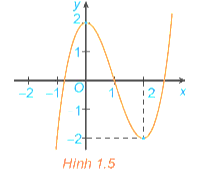
Luyện tập 1 trang 6 Toán 12 Tập 1: Hình 1.5 là đồ thị của hàm số y = x3 – 3x2 + 2. Hãy tìm các khoảng đồng biến, khoảng nghịch biến của hàm số.
Lời giải:
Tập xác định của hàm số là ℝ. Từ đồ thị suy ra:
Hàm số y = x3 – 3x2 + 2 đồng biến trên các khoảng (−∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
HĐ2 trang 7 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
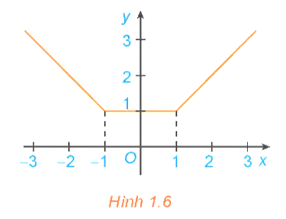
HĐ2 trang 7 Toán 12 Tập 1: Xét hàm số có đồ thị như hình 1.6
a) Xét dấu đạo hàm của hàm số trên các khoảng (−∞; −1), (1; +∞). Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu đạo hàm của hàm số trên mỗi khoảng này.
b) Có nhận xét gì về đạo hàm y' và hàm số y trên khoảng (−1;1)?
Lời giải:
a) +) Với x < −1, ta có y' = −1 < 0.
+) Với x > 1, ta có y' = 1 > 0.
Nhận xét:
+ Với x ∈ (−∞; −1), ta có y' < 0 thì hàm số nghịch biến.
+ Với x ∈ (1; +∞), ta có y' > 0 thì hàm số đồng biến.
b) Với x ∈ (−1;1) ta có y' = 0 thì hàm số y không đổi.
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Luyện tập 2 trang 7 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
Luyện tập 2 trang 7 Toán 12 Tập 1: Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số y = −x2 + 2x + 3.
Lời giải:
Tập xác định của hàm số là ℝ.
Có y' = −2x + 2.
y' > 0 với x ∈ (−∞; 1) và y' < 0 với x ∈ (1; +∞).
Do đó hàm số đồng biến trên khoảng (−∞; 1) và nghịch biến trên khoảng (1; +∞).
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
HĐ3 trang 7 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
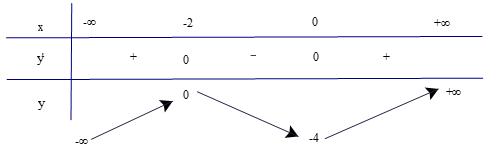
HĐ3 trang 7 Toán 12 Tập 1: Cho hàm số y = f(x) = x3 – 3x2 + 2x + 1.
a) Tính đạo hàm f'(x) và tìm các điểm x mà f'(x) = 0.
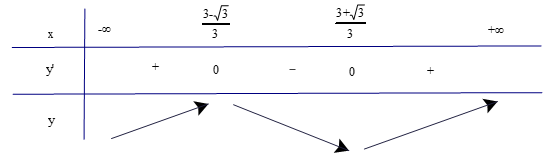
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
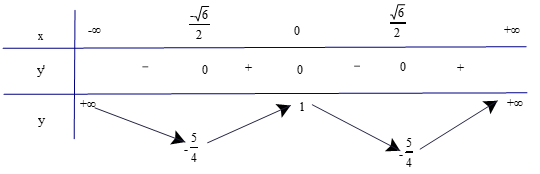
a) Có f'(x) = 3x2 – 6x + 2.
f’(x) = 0 3x2 – 6x + 2 = 0
b)
c) Hàm số đồng biến trên các khoảng và
Hàm số nghịch biến trên khoảng .
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Luyện tập 3 trang 9 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
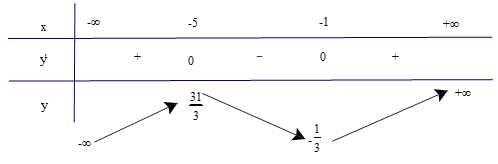
Luyện tập 3 trang 9 Toán 12 Tập 1: Tìm các khoảng đơn điệu của các hàm số sau:
a) b) .
Lời giải:
a) Tập xác định của hàm số là ℝ.
Ta có y' = x2 + 6x + 5; y' = 0 ⇔ x = −1 hoặc x = −5.
Lập bảng biến thiên của hàm số
Từ bảng biến thiên ta có:
Hàm số đồng biến trên các khoảng (−∞; −5) và (−1; +∞).
Hàm số nghịch biến trên khoảng (−5; −1).
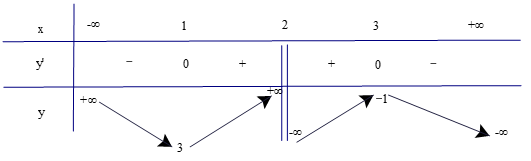
b) Tập xác định của hàm số là ℝ\{2}.
Có ;
y' = 0 ⇔ x = 3 hoặc x = 1.
Lập bảng biến thiên của hàm số
Từ bảng biến thiên ta có:
Hàm số đồng biến trên các khoảng (1; 2) và (2; 3).
Hàm số nghịch biến trên các khoảng (−∞; 1) và (3; +∞).
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Vận dụng 1 trang 9 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
Vận dụng 1 trang 9 Toán 12 Tập 1: Giải bài toán trong tình huống mở đầu bằng cách thực hiện lần lượt các yêu cầu sau:
Lời giải:
a) s(t) = t3 – 9t2 + 15t.
Có v(t) = s'(t) = 3t2 – 18t + 15.
b) Có v(t) > 0 ⇔ và v(t) < 0 ⇔ 1 < t < 5.
Do t ≥ 0 nên ta có:
Chất điểm chuyển động sang phải khi t ∈ (0; 1) và (5; +∞).
Chất điểm chuyển động sang trái khi t ∈ (1; 5).
Vậy chất điểm chuyển động sang phải trong khoảng thời gian từ 0 giây đến 1 giây hoặc trong khoảng thời gian lớn hơn 5 giây, chất điểm chuyển động sang trái trong khoảng thời gian từ 1 giây đến 5 giây.
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
HĐ4 trang 9 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
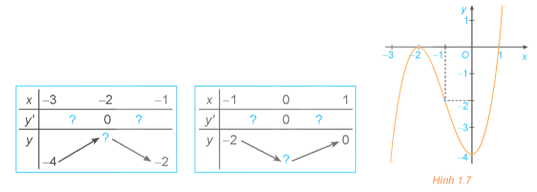
HĐ4 trang 9 Toán 12 Tập 1: Quan sát đồ thị của hàm số y = x3 + 3x2 – 4 (H.1.7). Xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở:
Lời giải:
Tập xác định của hàm số là ℝ.
Có y' = 3x2 + 6x; y' = 0 x = 0 hoặc x = −2.
Ta có bảng biến thiên
Dựa vào bảng biến thiên trên, ta có
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Luyện tập 4 trang 10 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
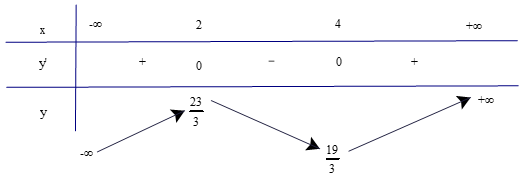
Luyện tập 4 trang 10 Toán 12 Tập 1: Hình 1.9 là đồ thị của hàm số y = f(x). Hãy tìm các cực trị của hàm số.
Lời giải:
Từ đồ thị ta có:
Hàm số đạt cực đại tại x = −1 và yCĐ = y(−1) = 5.
Hàm số đạt cực tiểu tại x = 1 và yCT = y(1) = 1.
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
HĐ5 trang 10 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
HĐ5 trang 10 Toán 12 Tập 1: Cho hàm số .
a) Tính đạo hàm f'(x) và tìm các điểm mà tại đó đạo hàm f'(x) = 0.
b) Lập bảng biến thiên của hàm số.
c) Từ bảng biến thiên suy ra các điểm cực trị của hàm số.
Lời giải:
a) Tập xác định của hàm số là ℝ.
Có y' = x2 – 6x + 8.
Có y' = 0 ⇔ x2 – 6x + 8 = 0 ⇔ x = 4 hoặc x = 2.
b) Ta có bảng biến thiên
c) Dựa vào bảng biến thiên ta có:
Hàm số đạt cực đại tại x = 2 và yCĐ = y(2) = .
Hàm số đạt cực tiểu tại x = 4 và yCT = y(4) = .
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Câu hỏi trang 11 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
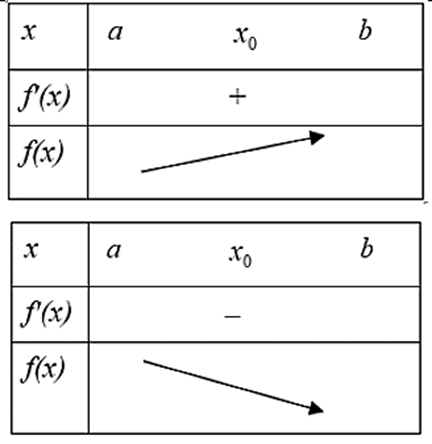
Câu hỏi trang 11 Toán 12 Tập 1: Giải thích vì sao nếu f'(x) không đổi dấu khi x qua x0 thì x0 không phải là điểm cực trị của hàm số f(x)?
Lời giải:
f'(x) không đổi dấu khi x qua x0, ta có bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy nếu f'(x) không đổi dấu khi x qua x0 thì x0 không phải là điểm cực trị của hàm số f(x).
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Luyện tập 5 trang 12 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
Luyện tập 5 trang 12 Toán 12 Tập 1: Tìm cực trị của các hàm số sau:
a) y = x4 – 3x2 + 1;
b) .
Lời giải:
a) Tập xác định của hàm số là ℝ.
Ta có y' = 4x3 – 6x; y' = 0 ⇔ x = 0 hoặc x = hoặc .
Lập bảng biến thiên của hàm số
Từ bảng biến thiên ta có:
Hàm số đạt cực tiểu tại và yCT = .
Hàm số đạt cực đại tại x = 0 và yCĐ = 1.
Hàm số đạt cực tiểu tại và yCT = .
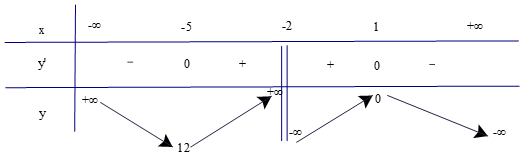
b) Tập xác định của hàm số là ℝ\{−2}.
Có .
Có y' = 0⇔ −x2 – 4x + 5 = 0 ⇔ x = 1 hoặc x = −5.
Lập bảng biến thiên của hàm số
Từ bảng biến thiên ta có:
Hàm số đạt cực tiểu tại x = −5 và yCT = 12.
Hàm số đạt cực đại tại x = 1 và yCĐ = 0.
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Vận dụng 2 trang 12 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
Vận dụng 2 trang 12 Toán 12 Tập 1: Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5 m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức
h(t) = 2 + 24,5t – 4,9t2.
Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Lời giải:
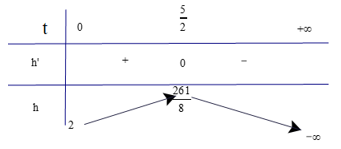
Tập xác định của hàm số là ℝ.
Có h'(t) = −9,8t + 24,5; h'(t) = 0 ⇔ .
Lập bảng biến thiên của hàm số
Dựa vào bảng biến thiên ta có tại thời điểm thì vật đạt độ cao lớn nhất là .
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Bài 1.1 trang 13 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
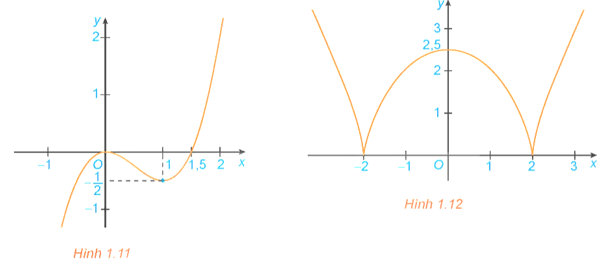
Bài 1.1 trang 13 Toán 12 Tập 1: Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
a) Đồ thị hàm số (H.1.11);
b) Đồ thị hàm số (H.1.12).
Lời giải:
a) Dựa vào đồ thị hàm số ta có:
Hàm số đồng biến trên các khoảng (−∞; 0) và (1; +∞).
Hàm số nghịch biến trên khoảng (0; 1).
b) Dựa vào đồ thị hàm số ta có:
Hàm số đồng biến trên các khoảng (−2; 0) và (2; +∞).
Hàm số nghịch biến trên các khoảng (−∞; −2) và (0; 2).
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Bài 1.2 trang 13 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
Bài 1.2 trang 13 Toán 12 Tập 1: Xét sự đồng biến, nghịch biến của các hàm số sau:
a) ;
b) y = −x3 + 2x2 – 5x + 3.
Lời giải:
a) Tập xác định của hàm số là ℝ.
Có y' = x2 – 4x + 3.
Hàm số đồng biến khi y' > 0 x2 – 4x + 3 > 0 .
Hàm số nghịch biến khi y' < 0 x2 – 4x + 3 < 0 1 < x < 3.
Do đó hàm số đồng biến trên các khoảng (−∞; 1) và (3; +∞); nghịch biến trên khoảng (1; 3).
b) Tập xác định của hàm số là ℝ.
Có y' = −3x2 + 4x – 5
Do đó hàm số luôn nghịch biến trên ℝ.
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Bài 1.3 trang 13 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
Bài 1.3 trang 13 Toán 12 Tập 1: Tìm các khoảng đơn điệu của các hàm số sau:
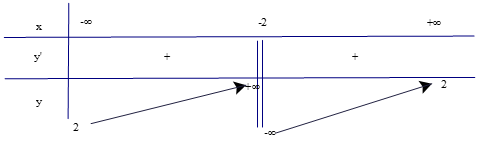
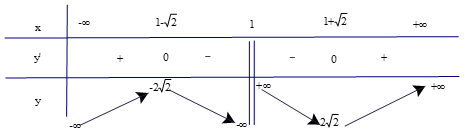
a) ; b) .
Lời giải:
a) Tập xác định của hàm số là ℝ\{−2}.
Có .
Lập bảng biến thiên của hàm số
Dựa vào bảng biến thiên ta có:
Hàm số đồng biến trên cách khoảng (−∞; −2) và (−2; +∞).
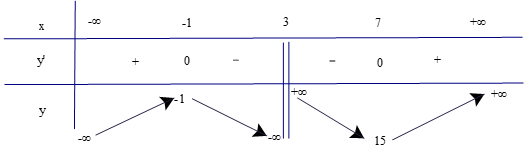
b) Tập xác định của hàm số là ℝ\{3}.
Có ;
Có y' = 0 ⇔ x2 – 6x – 7 = 0 ⇔ x = −1 hoặc x = 7.
Lập bảng biến thiên của hàm số
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng (−∞; −1) và (7; +∞).
Hàm số nghịch biến trên các khoảng (−1; 3) và (3; 7).
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Bài 1.4 trang 13 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
Bài 1.4 trang 13 Toán 12 Tập 1: Xét chiều biến thiên của các hàm số sau:
a) ;
b) .
Lời giải:
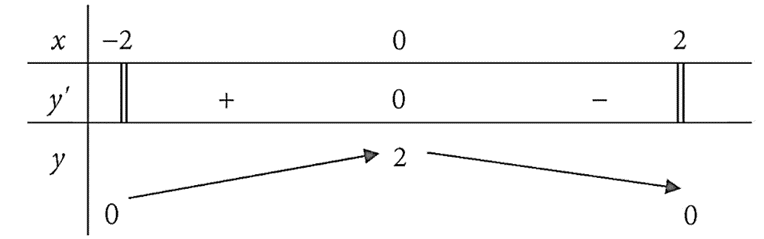
a) Tập xác định của hàm số là D = [−2; 2].
Có y' = 0 ⇔ x = 0.
Lập bảng biến thiên của hàm số
Dựa vào bảng biến thiên, ta có
Hàm số đồng biến trên khoảng (−2; 0) và nghịch biến trên khoảng (0; 2).
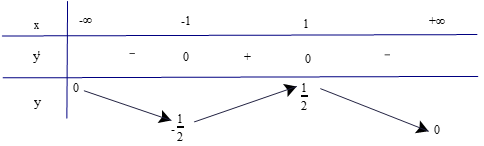
b) Tập xác định của hàm số là ℝ.
Có ; y' = 0 ⇔ −x2 + 1 = 0 ⇔ x = 1 hoặc x = −1.
Lập bảng biến thiên của hàm số
Dựa vào bảng biến thiên, ta có:
Hàm số đồng biến trên khoảng (−1; 1).
Hàm số nghịch biến trên các khoảng (−∞; −1) và (1; +∞).
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Bài 1.5 trang 13 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
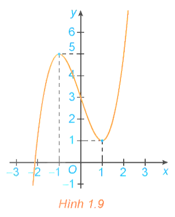
Bài 1.5 trang 13 Toán 12 Tập 1: Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số trong đó N(t) được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm N'(t) và . Từ đó, giải thích tại sao số dân của thị trấn đó luôn tăng nhưng sẽ không vượt quá một ngưỡng nào đó.
Lời giải:
a) Số dân vào năm 2000 (t = 0) của thị trấn đó là: nghìn người.
Sau 15 năm kể từ năm 2000 số dân của thị trấn đó là: .
Vậy số dân của thị trấn đó vào năm 2015 là 19250 người.
b) Có ;
Vì N'(t) > 0, ∀t do đó hàm số N(t) là hàm đồng biến hơn nữa do đó dân số của thị trấn đó sẽ không vượt quá 25 nghìn người.
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Bài 1.6 trang 14 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
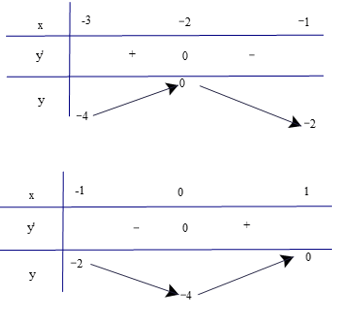
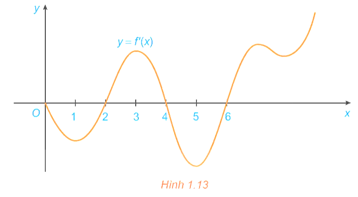
Bài 1.6 trang 14 Toán 12 Tập 1: Đồ thị của đạo hàm bậc nhất y = f'(x) của hàm số f(x) được cho trong hình 1.13.
a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.
b) Tại giá trị nào của x thì f(x) có cực đại và cực tiểu? Giải thích.
Lời giải:
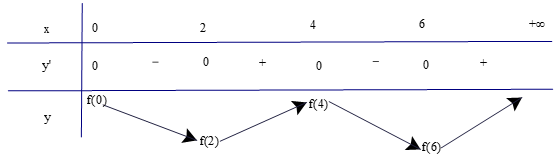
Dựa vào đồ thị của hàm y = f'(x), ta có bảng biến thiên của hàm số y = f(x) như sau
a) Dựa vào bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng (2; 4) và (6; +∞).
b) Dựa vào bảng biến thiên, ta có:
Hàm số đạt cực tiểu tại x = 2 và x = 6.
Hàm số đạt cực đại tại x = 4.
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Bài 1.7 trang 14 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
Bài 1.7 trang 14 Toán 12 Tập 1: Tìm cực trị của các hàm số sau:
a) y = 2x3 – 9x2 + 12x – 5;
b) y = x4 – 4x2 + 2;
c) ;
d)
Lời giải:
a) Tập xác định của hàm số là ℝ.
Có y' = 6x2 – 18x + 12; y' = 0 ⇔ x = 1 hoặc x = 2.
Lập bảng biến thiên của hàm số
Dựa vào bảng biến thiên, ta có
Hàm số đạt cực đại tại x = 1 và yCĐ = 0.
Hàm số đạt cực tiểu tại x = 2 và yCT = −1.
b) Tập xác định của hàm số là ℝ.
Có y' = 4x3 – 8x; y' = 0 ⇔ x = 0 hoặc hoặc .
Lập bảng biến thiên của hàm số
Dựa vào bảng biến thiên, ta có:
Hàm số đạt cực tiểu tại và yCT = −2.
Hàm số đạt cực đại tại x = 0 và yCĐ = 2.
Hàm số đạt cực tiểu tại và yCT = −2.
c) Tập xác định của hàm số là ℝ\{1}.
Có ;
Có y' = 0 ⇔ x2 – 2x – 1 = 0 hoặc .
Lập bảng biến thiên của hàm số
Dựa vào bảng biến thiên, ta có:
Hàm số đạt cực đại tại và .
Hàm số đạt cực tiểu tại và .
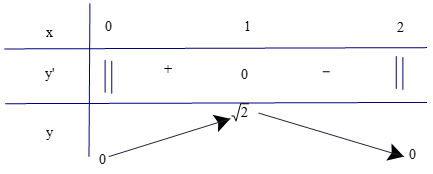
d) Tập xác định của hàm số là D = [0; 2].
Có .
Có y' = 0 ⇔ x = 1.
Lập bảng biến thiên của hàm số
Dựa vào bảng biến thiên ta có:
Hàm số đạt cực đại tại x = 1 và .
Hàm số không có cực tiểu.
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Bài 1.8 trang 14 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
Bài 1.8 trang 14 Toán 12 Tập 1: Cho hàm số y = f(x) = |x|.
a) Tính các giới hạn và .
Từ đó suy ra hàm số không có đạo hàm tại x = 0.
b) Sử dụng định nghĩa, chứng minh hàm số có cực tiểu tại x = 0 (xem hình 1.4).
Lời giải:
a)
Do nên hàm số không có đạo hàm tại x = 0.
b) Theo định nghĩa, hàm số f(x) đạt cực tiểu tại x = x0 nếu tồn tại số h > 0 sao cho f(x) > f(x0) với mọi x ∈ (x0 – h; x0 + h) và x ≠ x0 .
Ở đây, x0 = 0. Ta sẽ chứng minh rằng tồn tại số h > 0 sao cho f(x) > f(0) với mọi x ∈ (– h; h).
Với mọi x ∈ (– h; h), ta có |x| < h.
Mà |x| > 0, với mọi x ≠ 0. Do đó f(x) = |x| > 0 = f(0), với mọi x ∈ (– h; h) và x ≠ 0.
Vậy ta chứng minh được rằng với mọi x ∈ (– h; h) và x ≠ x0, f(x) > f(0). Điều này chứng tỏ rằng hàm số có cực tiểu tại x = 0.
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:
Bài 1.9 trang 14 Toán 12 Tập 1 - Kết nối tri thức
Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức
Bài 1.9 trang 14 Toán 12 Tập 1: Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f'(t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?
Lời giải:
Có .
Có .
Và . Do đó, doanh số luôn tăng nhưng sẽ không vượt quá 5 000.
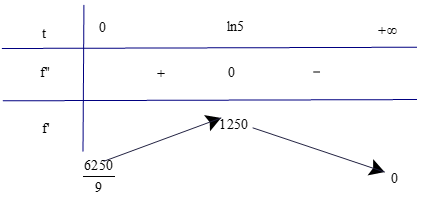
Có
Có f"(t) = 0 ⇔ 5 – et = 0 ⇔ t = ln5.
Ta có bảng biến thiên
Dựa vào bảng biến thiên, ta thấy f'(t) đạt giá trị lớn nhất tại t = ln5 ≈ 1,6 và .
Vậy sau khi phát hành sản phẩm khoảng 1,6 năm thì tốc độ bán hàng lớn nhất.
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác: