Với giải bài tập Toán 7 Bài 4: Làm tròn và ước lượng sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán 7 Bài 4:

Giải Toán 7 Cánh diều Bài 4: Làm tròn và ước lượng

Video Giải Toán 7 Bài 4: Làm tròn và ước lượng - Cô Ngô Thị Vân (Giáo viên VietJack)

Hoạt động khởi động

Giải Toán 7 trang 48 Tập 1

Khởi động trang 48 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Khởi động trang 48 Toán lớp 7 Tập 1: Khởi động trang 48 Toán 7 Tập 1 Cánh diều Hỏi diện tích của bồn hoa khoảng bao nhiêu mét vuông?

Lời giải:

Công thức tính diện tích hình tròn là: S = π.R² trong đó R là bán kính của hình tròn đó. 

Lấy π ≈ 3,14.

Diện tích bồn hoa là: 

S = π.(0,8)² ≈ 3,14 .0,8 .0,8 = 2,0096 (m²) ≈ 2 (m²)

Vậy diện tích bồn hoa khoảng 2 m².

Lời giải bài tập Toán 7 Bài 4: Làm tròn và ước lượng hay, chi tiết khác:

Hoạt động 1 trang 48 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Hoạt động 1 trang 48 Toán lớp 7 Tập 1: Hóa đơn tiền điện tháng 9/2020 của gia đình cô Hạnh là 574 880 đồng. Trong thực tế, cô Hạnh đã trả tiền mặt cho người thu tiền điện số tiền là 575 000 đồng. Tại sao cô Hạnh không thể trả cho người thu tiền điện số tiền chính xác là 574 880 đồng?

Lời giải:

Trên thực tế, hiện nay các đồng tiền có mệnh giá nhỏ nhất là 200 đồng nên số tiền 880 đồng sẽ không có mệnh giá tiền nào phù hợp để trả.

Do vậy cô Hạnh không thể trả chính xác số tiền 574 880 đồng bằng tiền mặt.

Lời giải bài tập Toán 7 Bài 4: Làm tròn và ước lượng hay, chi tiết khác:

Luyện tập 1 trang 48 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Luyện tập 1 trang 48 Toán lớp 7 Tập 1: Quãng đường từ sân vận động Old Trafford ở Greater Manchester đến tháp đồng hồ Big Ben ở London (Vương Quốc Anh) khoảng 200 dặm. (Nguồn: https://www.google.com/maps). Tính độ dài quãng đường đó theo đơn vị ki-lô-mét (làm tròn kết quả đến hàng đơn vị), biết 1 dặm = 1,609344 km. cách từ sân vận động Old Trafford ở Greater Manchester đến tháp đồng hồ Big Ben ở London (Vương Quốc Anh) là 201 dặm. (Nguồn: https://www.google.com). Tính khoảng cách đó theo đơn vị ki-lô-mét (làm tròn đến hàng đơn vị), biết 1 dặm = 1,609344 km.

Lời giải:

Quãng đường từ sân vận động Old Trafford ở Greater Manchester đến tháp đồng hồ Big Ben ở London (Vương Quốc Anh) theo đơn vị ki-lô-mét là khoảng:

200 . 1,609344 = 321,8688 ≈ 322 (km).

Vậy quãng đường đó dài khoảng 322 km.

Lời giải bài tập Toán 7 Bài 4: Làm tròn và ước lượng hay, chi tiết khác:

Hoạt động 2 trang 48 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Hoạt động 2 trang 48 Toán lớp 7 Tập 1: Làm tròn số 144 đến hàng chục. Trên trục số nằm ngang, tìm khoảng cách giữa điểm biểu diễn số làm tròn và điểm biểu diễn số ban đầu.

Lời giải:

Làm tròn số 144 đến hàng chục:

Nhận thấy chữ số ở hàng đơn vị là 4 < 5 nên ta giữ nguyên chữ số hàng chục và thay chữ số hàng đơn vị bằng số 0.

Vậy làm tròn số 144 đến hàng chục ta thu được kết quả là 140.

Biểu diễn 140 và 144 lên chục số ta được:

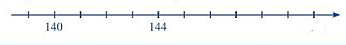
Ta thấy khoảng cách giữa điểm biểu diễn số làm tròn và điểm biểu diễn ban đầu cách nhau 4 đơn vị.

Lời giải bài tập Toán 7 Bài 4: Làm tròn và ước lượng hay, chi tiết khác:

Luyện tập 2 trang 49 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Luyện tập 2 trang 49 Toán lớp 7 Tập 1:

a) Làm tròn số 23 615 với độ chính xác 5.

b) Làm tròn số 187 638 với độ chính xác 50.

Lời giải:

a) Vì 1 < 5 < 10 nên ta làm tròn số 23 615 đến hàng chục.

Gạch chân dưới chữ số hàng chục: 23 615.

Nhận thấy chữ số hàng đơn vị là 5 nên ta tăng thêm chữ số hàng chục một đơn vị và thay chữ số hàng đơn vị bởi số 0.

Vậy số 23 615 làm tròn với độ chính xác 5 ta thu được kết quả là 23 620.

b) Vì 10 < 50 < 100 nên ta làm tròn số 187 638 đến hàng trăm.

Gạch chân dưới chữ số hàng trăm: 187 638 .

Nhận thấy chữ số hàng chục là 3 < 5 nên ta giữ nguyên chữ số hàng trăm và thay các chữ số hàng chục và hàng đơn vị bởi số 0.

Vậy số 187 638 làm tròn với độ chính xác 50 ta thu được kết quả là 187 600.

Lời giải bài tập Toán 7 Bài 4: Làm tròn và ước lượng hay, chi tiết khác:

Luyện tập 3 trang 51 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Luyện tập 3 trang 51 Toán lớp 7 Tập 1: Áp dụng quy tắc làm tròn số để ước lượng kết quả của mỗi phép tính sau:

a) 18,25 + 11,98;

b) 11,91 – 2,49;

c) 30,09.(–29,87)

Lời giải:

a) Làm tròn số 18,25 đến hàng đơn vị ta được số là 18; làm tròn số 11,98 đến hàng đơn vị ta được số là 12.

Khi đó ta ước lượng kết quả phép tính 18,25 + 11,98 là 18,25 + 11,98 ≈ 18 + 12 = 30.

Vậy kết quả của phép tính 18,25 + 11,98 gần với 30.

b) Làm tròn số 11,91 đến hàng phần mười ta được số 11,9; làm tròn số 2,49 đến hàng phần mười ta được số 2,5.

Khi đó ta ước lượng kết quả phép tính 11,91 – 2,49 là 11,91 – 2,49 ≈ 11,9 – 2,5 = 9,4.

Vậy kết quả của phép tính 11,91 – 2,49 gần với 9,4.

c) Làm tròn số 30,09 đến hàng đơn vị ta được số 30; làm tròn số (-29,87) đến hàng đơn vị ta thu được kết quả là –30.

Khi đó ta ước lượng kết quả phép tính 30,09.(–29,87) là 30,09.(–29,87) ≈ 30.(–30) = –900.

Vậy kết quả của phép tính 30,09.(–29,87) gần với –900.

Lời giải bài tập Toán 7 Bài 4: Làm tròn và ước lượng hay, chi tiết khác:

Bài 1 trang 51 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Bài 1 trang 51 Toán lớp 7 Tập 1: Làm tròn số 98 176 244 với độ chính xác là 50.

Lời giải:

Vì 10 < 50 < 100 nên ta làm tròn số 98 176 244 đến hàng trăm.

Gạch chân dưới chữ số hàng trăm: 98 176 244. 

Nhận thấy chữ số hàng chục là 4 < 5 nên ta giữ nguyên chữ số hàng trăm và thay các chữ số hàng chục, hàng đơn vị bởi chữ số 0.

Khi đó số 98 176 244 làm tròn đến hàng trăm ta thu được kết quả là 98 176 200.

Vậy số 98 176 244 làm tròn với độ chính xác 50 ta thu được kết quả là 98 176 200.

Lời giải bài tập Toán 7 Bài 4: Làm tròn và ước lượng hay, chi tiết khác:

Bài 2 trang 51 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Bài 2 trang 51 Toán lớp 7 Tập 1:

a) Làm tròn số 4,76908 với độ chính xác 0,5.

b) Làm tròn số –4,76908 với độ chính xác 0,05.

Lời giải:

a) Vì 0,1 < 0,5 < 1 nên ta sẽ làm tròn số 4,76908 đến hàng đơn vị.

Gạch chân dưới chữ số hàng đơn vị 4,76908. 

Nhận thấy chữ số ở hàng phần mười là 7 > 5 nên ta tăng thêm chữ số hàng đơn vị một đơn vị. Phần các chữ số đằng sau hàng đơn vị là phần thập phân nên ta bỏ đi.

Khi đó, số 4,76908 làm tròn đến hàng đơn vị ta thu được kết quả là 5.

Vậy số 4,76908 làm tròn với độ chính xác là 0,5 ta thu được kết quả là 5.

b) Vì 0,01 < 0,05 < 0,1 nên ta sẽ làm tròn số –4,76908 đến hàng phần mười.

Gạch chân dưới chữ số hàng phần mười –4,76908. 

Nhận thấy chữ số ở hàng phần trăm là 6 > 5 nên ta tăng thêm chữ số hàng phần mười một đơn vị. Phần các chữ số đằng sau hàng phần mười ta bỏ đi.

Khi đó, số –4,76908 làm tròn đến hàng phần mười ta thu được kết quả là –4,8.

Vậy số –4,76908 làm tròn với độ chính xác là 0,05 ta thu được kết quả là –4,8.

Lời giải bài tập Toán 7 Bài 4: Làm tròn và ước lượng hay, chi tiết khác:

Bài 3 trang 51 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Bài 3 trang 51 Toán lớp 7 Tập 1:

a) Sử dụng máy tính cầm tay để tính rồi viết mỗi số sau dưới dạng số thập phân vô hạn (tuần hoàn hoặc không tuần hoàn): $\frac{17}{3};-\frac{125}{111};\sqrt{5};\sqrt{19}$.

b) Làm tròn số $\sqrt{19}$ với độ chính xác 0,05.

Lời giải:

a) Sử dụng máy tính cầm tay ta được:

$\frac{17}{3}=\mathrm{5,66666...}$

Nhận thấy kết quả nhận được có chu kì là 6 nên ta có $\frac{17}{3}=\mathrm{5,66666...}$= 5, (6)

$-\frac{125}{111}=-\mathrm{1,126126126...}$

Nhận thấy kết quả nhận được có chu kì là 126 nên ta có:

$-\frac{125}{111}=-\mathrm{1,126126126...}=-\mathrm{1,}\left(126\right)$

$\sqrt{5}=\mathrm{2,2360679...}$

$\sqrt{19}=\mathrm{4,35889894...}$

b) Theo câu a ta có $\sqrt{19}=\mathrm{4,35889894...}$

Ta có: 0,01 < 0,05 < 0,1 nên để làm tròn số trên đến 0,05 ta sẽ làm tròn đến hàng phần mười.

Gạch chân dưới chữ số hàng phần mười 4,35889894…. 

Nhận thấy chữ số ở hàng phần trăm là 5 nên ta tăng thêm chữ số hàng phần mười một đơn vị. Phần các chữ số đằng sau hàng phần mười ta bỏ đi.

Khi đó, số 4,35889894… làm tròn đến phần mười ta thu được kết quả là 4,4.

Vậy số $\sqrt{19}$ làm tròn với độ chính xác là 0,05 ta thu được kết quả là 4,4.

Lời giải bài tập Toán 7 Bài 4: Làm tròn và ước lượng hay, chi tiết khác:

Bài 4 trang 51 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Bài 4 trang 51 Toán lớp 7 Tập 1: Áp dụng quy tắc làm tròn số để ước lượng kết quả của mỗi phép tính sau: 

a) (–28,29) + (–11,91)

b) 43,91 – 4,49

c) 60,49.(–19,51)

Lời giải:

a) (–28,29) + (–11,91)

Làm tròn số –28,29 đến hàng đơn vị ta được số –28; làm tròn số –11,91 đến hàng đơn vị ta được số –12.

Khi đó kết quả phép tính của hai số đã làm tròn là (–28) + (–12) = –40.

Vậy kết quả của phép tính (–28,29) + (–11,91) gần với –40.

b) 43,91 – 4,49

Làm tròn số 43,91 đến hàng phần mười ta được số 43,9; làm tròn số 4,49 đến hàng phần mười ta được số 4,5.

Khi đó kết quả phép tính hai số đã làm tròn là: 43,9 – 4,5 = 39,4.

Vậy kết quả của phép tính 43,91 – 4,5 gần với 39,4.

c) 60,49.(–19,51)

Làm tròn số 60,49 đến hàng đơn vị ta được số 60; làm tròn số –19,51 đến hàng đơn vị ta được số –20.

Khi đó kết quả phép tính hai số đã làm tròn là: 60.(–20) = –1200.

Vậy kết quả của phép tính 60,49.(–19,51) gần với –1200.

Lời giải bài tập Toán 7 Bài 4: Làm tròn và ước lượng hay, chi tiết khác:

Bài 5 trang 51 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Bài 5 trang 51 Toán lớp 7 Tập 1: Các nhà khoa học tính được vận tốc ánh sáng bằng 299 792 458 m/s. Để dễ nhớ, người ta nói vận tốc ánh sáng là 300 000 000 m/s. Số liệu đó đã được làm tròn đến hàng nào?

Lời giải:

Độ chính xác d là: 

300 000 000 – 299 792 458 = 207 542

Vì 100 000 < 207 542 < 1 000 000 nên số liệu đã được làm tròn đến hàng triệu.

Vậy số liệu đó đã được làm tròn đến hàng triệu.

Lời giải bài tập Toán 7 Bài 4: Làm tròn và ước lượng hay, chi tiết khác:

Sách bài tập Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Với giải sách bài tập Toán 7 Bài 4: Làm tròn số và ước lượng sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 4.

Giải sách bài tập Toán 7 Bài 4: Làm tròn số và ước lượng - Cánh diều

Giải SBT Toán 7 trang 49 Tập 1

Vở bài tập Toán 7 Bài 4: Làm tròn và ước lượng - Cánh diều

Với giải vở bài tập Toán lớp 7 Bài 4: Làm tròn và ước lượng sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VBT Toán 7 Bài 4.

Giải vở bài tập Toán 7 Bài 4: Làm tròn và ước lượng - Cánh diều

I. Kiến thức trọng tâm

Giải VBT Toán 7 trang 43 Tập 1

Làm tròn và ước lượng (Lý thuyết Toán lớp 7) - Cánh diều

Với tóm tắt lý thuyết Toán 7 Bài 4: Làm tròn và ước lượng hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Làm tròn và ước lượng (Lý thuyết Toán lớp 7) - Cánh diều

Lý thuyết Làm tròn và ước lượng

1. Làm tròn số

1.1 Số làm tròn

Ở nhiều tình huống thực tiễn ta cần tìm một số thực khác xấp xỉ với số thực đã cho để thuận tiện hơn trong ghi nhớ, đo đạc, hay tính toán. Số thực tìm được như thế được gọi là số làm tròn của số thực đã cho.

Ví dụ:

Hóa đơn tiền điện của gia đình bạn An tháng 9/2021 là 356 870 đồng. Trên thực tế mẹ của An đã trả tiền mặt cho người thu tiền điện 357 000 đồng.

Vậy số 357 000 là số làm tròn của số 356 870.

1.2 Làm tròn số với độ chính xác cho trước

Ta nói số a được làm tròn đến số b với độ chính xác d nếu khoảng cách giữa điểm a và điểm b trên trục số không vượt quá d.

Ví dụ: Làm tròn số 126 đến hàng chục ta được số 130. Khoảng cách giữa hai điểm 126 và 130 trên trục số là 130 – 126 = 4. Khoảng cách này không vượt quá 5. Khi đó ta nói số 126 được làm tròn đến số 130 với độ chính xác 5.

Nhận xét:

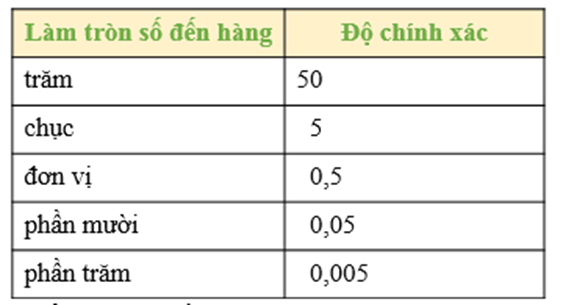
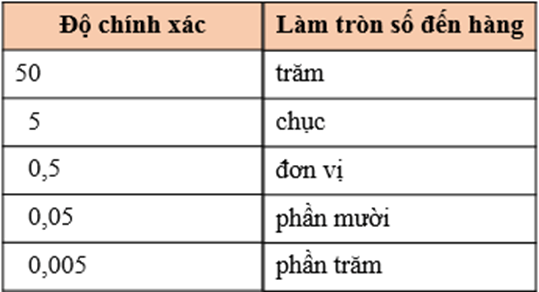
- Khi làm tròn số đến một hàng nào đó thì độ chính xác bằng nửa đơn vị của hàng làm tròn.

- Để làm tròn số với độ chính xác cho trước, ta có thể sử dụng cách ở bảng sau:

- Để làm tròn một số thập phân âm, ta chỉ cần làm tròn số đối của nó rồi đặt dấu “–” trước kết quả.

Ví dụ:

a) Làm tròn số 3,141592653… đến hàng phần trăm.

b) Làm tròn số 128,25 với độ chính xác 0,05.

c) Làm tròn số – 1,9254 với độ chính xác 0,005

d) Làm tròn số $\sqrt{2}$ với độ chính xác 0,5.

Hướng dẫn giải

a) Ta áp dụng quy tắc làm tròn số thập phân hữu hạn. Do chữ số ở hàng phần nghìn là 1 < 5 nên 3,141592653… ≈ 3,14.

Người ta chứng minh được rằng số 3,141592653… làm tròn đến 3,14 cũng với độ chính xác 0,005.

b) Để làm tròn số 128,25 với độ chính xác 0,05 ta sẽ làm tròn đến hàng phần mười. Áp dụng quy tắc làm tròn số ta được 128,25 ≈ 128,3.

c) Để làm tròn số –1,9254 với độ chính xác 0,005 ta sẽ làm tròn đến hàng phần trăm. Áp dụng quy tắc làm tròn số ta được 1,9254 ≈ 1,93. Vì vậy, – 1,9254 ≈ –1,93.

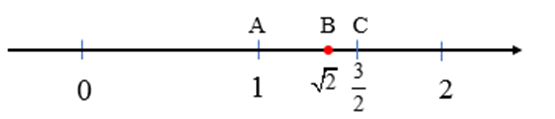
d)

Ta biểu diễn số $\sqrt{2}$ trên trục số. Khi đó AC = 0,5, điểm B nằm giữa A và C nên AB < AC.

Mà AC = 0,5 nên AB < 0,5, tức là khoảng cách giữa điểm $\sqrt{2}$ và điểm 1 trên trục số nhỏ hơn 0,5. Vậy với độ chính xác 0,5 thì $\sqrt{2}$ ≈ 1.

Chú ý: Trong đo đạc và tính toán thực tiễn, ta thường có gắng làm tròn số thực với độ chính xác d nhỏ nhất càng tốt. Trong thực tế, làm tròn số thực là một công việc có nhiều khó khăn. Tuy nhiên, người ta cũng biết một số cách để làm tròn số thực.

2. Ước lượng

Trong thực tiễn, đôi lúc ta không quá quan tâm đến tính chính xác của kết quả tính toán mà chỉ cần ước lượng kết quả, tức là tìm một số gần sát với kết quả chính xác.

Ví dụ: Áp dụng quy tắc làm tròn để ước lượng kết quả của các phéo tính sau:

a) 5,14 + 4,93

b) 60,3 . 49,5

Hướng dẫn giải

a) Làm tròn đến hàng phần mười của mỗi số hạng: 5,14 ≈ 5,1; 4,93 ≈ 4,9

Khi đó 5,14 + 4, 93 ≈ 5,1 + 4,9 = 10.

b) Làm tròn đến hàng đơn vị mỗi thừa số ta có: 60,3 ≈ 60; 49,5 ≈ 50.

Khi đó 60,3 . 49,5 ≈ 60 . 50 = 3000.

Bài tập Làm tròn và ước lượng

Bài 1:

a) Làm tròn số 43 258 với độ chính xác 500;

b) Làm tròn số 81,934 với độ chính xác 0,5.

Hướng dẫn giải

a) Để làm tròn số 43 258 với độ chính xác 500 ta sẽ làm tròn đến hàng nghìn. Áp dụng quy tắc làm tròn số ta có 43 258 ≈ 43 000.

b) Để làm tròn số 81,934 với độ chính xác 0,5 ta sẽ làm tròn đến hàng đơn vị. Áp dụng quy tắc làm tròn số ta có 81, 934 ≈ 82.

Bài 2: Áp dụng quy tắc làm tròn số để ước lượng kết quả của mỗi phép tính sau

a) ( –34,17) + (– 65,83);

b) (– 19,641) . (–29,613).

Hướng dẫn giải

a) Ta làm tròn hai số hạng đến hàng phần mười ta có –34,17 ≈ –34,2; – 65,83 ≈ – 65,8.

Khi đó (–34,17) + (–65,83) ≈ (–34,2) + (–65,8) = –100.

b) Ta làm tròn hai thừa số đến hàng đơn vị, ta có: – 19,641 ≈ –20; –29,613 ≈ –30.

Vậy (– 19,641) . (–29,613) ≈ (–20).(–30) = 600.

Học tốt Làm tròn và ước lượng

Các bài học để học tốt Làm tròn và ước lượng Toán lớp 7 hay khác:

15 Bài tập Làm tròn và ước lượng (có đáp án) - Cánh diều Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Làm tròn và ước lượng Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Làm tròn và ước lượng (có đáp án) - Cánh diều Trắc nghiệm Toán 7

Câu 1. Làm tròn số 9,375 đến hàng phần mười ta được kết quả là:

A. 9,3;

B. 9,4;

C. 9,37;

D. 9,38.

Câu 2. Làm tròn số 14,11 đến hàng đơn vị ta được số nào?

A. 14;

B. 14,1;

C. 14,2;

D. 15.

Câu 3. Làm tròn một số với độ chính xác 0,0005 tức là làm tròn đến hàng:

A. hàng đơn vị;

B. hàng phần mười;

C.hàng phần trăm;

D.hàng phần nghìn.

Câu 4. Làm tròn số 576 123 với độ chính xác 5 000 ta được:

A. 580 000;

B. 576 000;

C. 570 000;

D. 600 000.

Câu 5. Làm tròn số 1,(02) với độ chính xác 0,005 ta được:

A. 1,0;

B. 1,02;

C. 1,1;

D. 1,021.

Câu 6. Biết $\sqrt{11}=3,31662479...$ Làm tròn số $\sqrt{11}$ với độ chính xác 0,005 ta được:

A. 3,3;

B. 3,31;

C. 3,32;

D. 3,4.

Câu 7. Vào một ngày tháng 3 năm 2022, xăng dầu có giá 27 798 đồng/ lít. Một người đi xe máy muốn đổ xăng cho chiếc xe của mình nên đã làm tròn giá xăng là 30 000 đồng/ lít để ước lượng giá tiền mình cần trả để đổ xăng. Hỏi người đó đã làm tròn giá xăng đến hàng nào?

A. Hàng chục;

B. Hàng trăm;

C. Hàng nghìn;

D. Hàng chục nghìn;

Câu 8. Các nhà khoa học tính được vận tốc ánh sáng bằng 299 792 458 m/s. Để dễ nhớ, người ta nói vận tốc ánh sáng là 300 000 000 m/s. Số liệu đã được làm tròn với độ chính xác là bao nhiêu?

A. 5 000;

B. 50 000;

C. 500 000;

D. 5 000 000.

Câu 9. Cho các điểm biểu diễn các số trên trục số như hình vẽ sau:

Biết $\sqrt{10}=3,16227766...$

Số $\sqrt{10}$ khi làm tròn với độ chính xác 0,5 thì được biểu diễn bởi điểm nào?

A. Điểm A;

B. Điểm B;

C. Điểm C.

D. Không được biểu diễn bởi điểm nào.

Câu 10. Thực hiện phép tính (11,253 + 2,5) – (7,253 – 5,25) rồi làm tròn kết quả với độ chính xác 0,05 ta được kết quả là:

A. 11,7;

B. 12;

C. 11,75;

D. 11,8.

Câu 11. Áp dụng quy tắc làm tròn số để ước lượng kết quả phép tính: 31,12 – (–11,07)

A. 20,05;

B. 20;

C. 42,19;

D. 42.

Câu 12. Ước lượng kết quả của phép tính$\frac{4,87+2,8}{2,3+1,9}$:

A. 2;

B. 3;

C. $\frac{8}{5}$;

D. $\frac{8}{3}$.

Câu 13. Kết quả của phép tính 2,123.10,09 – 5,29.4,98 sau khi được ước lượng là:

A. –5;

B. –1;

C. 1;

D. –3.

Câu 14. Diện tích hình vuông có độ dài cạnh là 12,3 cm (làm tròn kết quả với độ chính xác 5) ta được:

A. 151 cm²;

B. 151,3 cm²;

C. 151,29 cm²;

D. 150 cm².

Câu 15. Người ta muốn sơn một bức tường hình chữ nhật với chiều dài 4,8 m và chiều rộng 3,2 m. Hãy ước lượng diện tích bức tường cần sơn.

A. 15,36 m²;

B. 15 m²;

C. 12 m²;

D. 16 m².

Xem thêm bài tập trắc nghiệm Toán lớp 7 Cánh diều có đáp án hay khác: