Với giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán Hình 7 Bài 14.

Giải Toán 7 Kết nối tri thức Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Video Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Cô Trần Thị Ngọc Anh (Giáo viên VietJack)

Mở đầu

Giải Toán 7 trang 70 Tập 1

Mở đầu trang 70 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Mở đầu trang 70 Toán 7 Tập 1: Trong thực tế, nhiều khi ta không thể đo được hết các cạnh của hai tam giác để khẳng định được chúng có bằng nhau hay không. Khi đó, có cách nào khác giúp ta biết được điều đó?

Sau bài toán này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Lời giải:

Chúng ta có thêm 2 cách khác để chứng minh hai tam giác bằng nhau như sau:

- Cách 1: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

- Cách 2: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

HĐ1 trang 70 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

HĐ1 trang 70 Toán 7 Tập 1: Vẽ $\widehat{xAy}=60°.$ Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4 cm, AC = 3 cm.

Nối điểm B với điểm C ta được tam giác ABC (H.4.27). Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC.

Lời giải:

Dùng thước thẳng có vạch chia ta đo được độ dài cạnh BC của tam giác ABC xấp xỉ  3,6 cm.

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

HĐ2 trang 70 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

HĐ2 trang 70 Toán 7 Tập 1: Vẽ thêm tam giác $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ với $\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}=60°,A^{\text{'}}{B}^{\text{'}}=4cm$ và $A^{\text{'}}{C}^{\text{'}}=3cm$ (H.4.28).

Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác ABC và $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}.$

- Hai tam giác ABC và $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ có bằng nhau không?

- Độ dài các cạnh BC và B'C'của hai tam giác em vừa vẽ có bằng các cạnh BC và B'C' của hai tam giác các bạn khác vẽ không?

- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?

Lời giải:

Thực hiện tương tự trong Hoạt động 1, ta vẽ hình như sau:

Bước 1. Vẽ $\widehat{x^{\text{'}}{A}^{\text{'}}{y}^{\text{'}}}=60°.$

Bước 2. Lấy điểm $B^{\text{'}}$ trên $A^{\text{'}}{y}^{\text{'}}$ sao cho $A^{\text{'}}{B}^{\text{'}}=4cm$ và lấy điểm $C^{\text{'}}$ trên $A^{\text{'}}{x}^{\text{'}}$ sao cho $A^{\text{'}}{C}^{\text{'}}=3cm.$

Bước 3. Nối điểm $B^{\text{'}}$ và $C^{\text{'}}$ ta được tam giác $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}.$

Dùng thước thẳng có vạch chia ta đo được:

AB = A'B' = 4cm, AC = A'C' = 3cm, BC = B'C' ≈ 3,6 cm

- Xét hai tam giác ABC và $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ có:

$AB=A^{\text{'}}{B}^{\text{'}}$ (chứng minh trên).

$BC=B^{\text{'}}{C}^{\text{'}}$ (chứng minh trên).

$AC=A^{\text{'}}{C}^{\text{'}}$ (chứng minh trên).

Do đó $\Delta ABC=\Delta A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ (c – c – c).

- Độ dài các cạnh BC và B'C' của hai tam giác em vừa vẽ bằng các cạnh BC và B'C' của hai tam giác các bạn khác vẽ.

- Hai tam giác em vừa vẽ bằng hai tam giác mà các bạn khác vẽ.

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

Câu hỏi trang 71 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Câu hỏi trang 71 Toán 7 Tập 1: Trong Hình 4.29, hai tam giác nào bằng nhau?

Lời giải:

Hai tam giác DEF và GHK có góc D không phải góc xen giữa hai cạnh EF, FD và góc G không phải góc xen giữa hai cạnh GH, HK nên ta không thực hiện xét hai tam giác này.

Xét hai tam giác ABC và MNP có:

AB = MN (theo giả thiết).

$\widehat{BAC}=\widehat{NMP}$ (theo giả thiết).

AC = MP (theo giả thiết).

Do đó $\Delta ABC=\Delta MNP$ (c – g – c).

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

Luyện tập 1 trang 71 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Luyện tập 1 trang 71 Toán 7 Tập 1: Hai tam giác ABC và MNP trong Hình 4.31 có bằng nhau không? Vì sao?

Lời giải:

Xét tam giác MNP có $\widehat{M}+\widehat{N}+\widehat{P}=180°.$

Do đó $\widehat{M}=180°-\widehat{N}-\widehat{P}=180°-50°-70°=60°.$

Xét hai tam giác ABC và MNP có:

AB = MN (theo giả thiết).

$\widehat{BAC}=\widehat{NMP}$ (cùng bằng 60^o).

AC = MP (theo giả thiết).

Vậy $\Delta ABC=\Delta MNP$ (c – g – c).

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

Vận dụng trang 71 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Vận dụng trang 71 Toán 7 Tập 1: Cho Hình 4.32, biết $\widehat{OAB}=\widehat{O\text{D}C},$ OA = OD và AB = CD. Chứng minh rằng:

a) AC = DB;

b) $\Delta OAC=\Delta O\text{DB.}$

Lời giải:

a) Do AB = CD nên AB + BC = CD + BC.

hay AC = DB.

Vậy AC = DB.

b) Xét hai tam giác OAC và ODB có:

OA = OD (theo giả thiết).

$\widehat{OAC}=\widehat{O\text{D}B}$ (theo giả thiết).

AC = BD (chứng minh trên).

Vậy $\Delta OAC=\Delta O\text{D}B$ (c – g – c).

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

HĐ3 trang 72 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

HĐ3 trang 72 Toán 7 Tập 1: Vẽ đoạn thẳng BC = 3 cm. Vẽ hai tia Bx và Cy sao cho $\widehat{xBC}=80°,\widehat{yCB}=40°$ như Hình 4.33.

Lấy giao điểm A của hai tia Bx và Cy, ta được tam giác ABC (H.4.33). Dùng thước thẳng có vạch chia đo độ dài hai cạnh AB, AC của tam giác ABC.

Lời giải:

Dùng thước thẳng có vạch chia, ta đo được độ dài cạnh AB xấp xỉ 2,2 cm và độ dài cạnh AC xấp xỉ 3,4 cm.

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

HĐ4 trang 72 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

HĐ4 trang 72 Toán 7 Tập 1: Vẽ thêm tam giác $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ sao cho $B^{\text{'}}{C}^{\text{'}}=3cm,\widehat{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=80°,\widehat{A^{\text{'}}{C}^{\text{'}}{B}^{\text{'}}}=40°$ (H.4.34).

Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác ABC và $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}.$ Hai tam giác ABC và $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ có bằng nhau không?

Lời giải:

Tương tự Hoạt động 3, ta vẽ hình như sau:

Bước 1. Vẽ đoạn thẳng $B^{\text{'}}{C}^{\text{'}}=3cm.$

Bước 2. Dùng thước đo độ, vẽ hai tia $B^{\text{'}}{x}^{\text{'}}$ và $C^{\text{'}}{y}^{\text{'}}$ sao cho $\widehat{x^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=80°,\widehat{y^{\text{'}}{C}^{\text{'}}{B}^{\text{'}}}=40°.$

Bước 3. Lấy giao điểm $A^{\text{'}}$ của hai tia $B^{\text{'}}{x}^{\text{'}}$ và $C^{\text{'}}{y}^{\text{'}}$ ta được tam giác $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}.$

- Dùng thước thẳng có vạch chia, ta đo được AB = A'B' ≈ 2,2 cm; AC = A'C' ≈ 3,4cm và BC = B'C' = 3cm.

- Xét hai tam giác ABC và $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ có:

$AB=A^{\text{'}}{B}^{\text{'}}$ (chứng minh trên).

$\widehat{ABC}=\widehat{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}$ (cùng bằng 80^o).

BC = B'C' (chứng minh trên).

Vậy $\Delta ABC=\Delta A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ (c – g – c).

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

Câu hỏi trang 72 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Câu hỏi trang 72 Toán 7 Tập 1: Hai tam giác nào trong Hình 4.35 bằng nhau?

Lời giải:

Tam giác GHK có góc H không phải góc kề của cạnh GK và tam giác DEF có góc F không phải góc kề của cạnh DE nên ta không xét hai tam giác này.

Xét hai tam giác ABC và MNP có:

$\widehat{ABC}=\widehat{MNP}$ (cùng bằng 50^o).

BC = NP (theo giả thiết).

$\widehat{ACB}=\widehat{MPN}$ (cùng bằng 70^o).

Vậy $\Delta ABC=\Delta MNP$ (g – c – g).

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

Luyện tập 2 trang 73 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Luyện tập 2 trang 73 Toán 7 Tập 1: Chứng minh hai tam giác ABD và CBD trong Hình 4.37 bằng nhau.

Lời giải:

Xét hai tam giác ABD và CBD có:

$\widehat{AB\text{D}}=\widehat{CB\text{D}}$ (theo giả thiết).

BD chung.

$\widehat{A\text{D}B}=\widehat{C\text{D}B}$ (theo giả thiết).

Vậy $\Delta AB\text{D}=\Delta CB\text{D}$ (g – c – g).

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

Thử thách nhỏ trang 73 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Thử thách nhỏ trang 73 Toán 7 Tập 1: Bạn Lan nói rằng: “Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau” (H.4.38). Theo em bạn Lan nói có đúng không? Vì sao?

Lời giải:

Xét tam giác ABC có $\widehat{BAC}+\widehat{ABC}+\widehat{BCA}=180°.$

Do đó  $\widehat{BCA}=180°-\widehat{BAC}-\widehat{ABC}$(1).

Xét tam giác $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ có $\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}+\widehat{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}+\widehat{B^{\text{'}}{C}^{\text{'}}{A}^{\text{'}}}=180°.$

Do đó $\widehat{B^{\text{'}}{C}^{\text{'}}{A}^{\text{'}}}=180°-\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}-\widehat{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}$ (2).

Mà $\widehat{BAC}=\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}},\widehat{ABC}=\widehat{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}$ (theo giả thiết) nên từ (1) và (2) ta có $\widehat{BCA}=\widehat{B^{\text{'}}{C}^{\text{'}}{A}^{\text{'}}}.$

Xét hai tam giác ABC và $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ có:

$\widehat{BAC}=\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}$ (theo giả thiết).

$AC=A^{\text{'}}{C}^{\text{'}}$ (theo giả thiết).

$\widehat{BCA}=\widehat{B^{\text{'}}{C}^{\text{'}}{A}^{\text{'}}}$ (chứng minh trên).

Do đó $\Delta ABC=\Delta A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ (g – c – g).

Vậy Lan nói đúng.

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

Bài 4.12 trang 73 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Bài 4.12 trang 73 Toán 7 Tập 1: Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.

Lời giải:

Xét Hình 4.39a.

Xét hai tam giác ABD và CDB có:

AB = CD (theo giả thiết).

$\widehat{AB\text{D}}=\widehat{C\text{D}B}$ (theo giả thiết).

BD chung.

Vậy $\Delta AB\text{D}=\Delta C\text{D}B$ (c – g – c).

Xét Hình 4.39b.

Xét hai tam giác AOD và COB có:

OA = OC (theo giả thiết).

$\widehat{AO\text{D}}=\widehat{COB}$ (2 góc đối đỉnh).

OD = OB (theo giả thiết).

Vậy $\Delta AO\text{D}=\Delta COB$ (c – g – c).

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

Bài 4.13 trang 73 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Bài 4.13 trang 73 Toán 7 Tập 1: Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.

a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau.

b) Chứng minh rằng $\Delta DAB=\Delta BC\text{D}.$

Lời giải:

a) Xét hai tam giác AOD và COB có:

OA = OC (theo giả thiết).

$\widehat{AO\text{D}}=\widehat{COB}$ (2 góc đối đỉnh).

OD = OB (theo giả thiết).

Vậy $\Delta AO\text{D}=\Delta COB$ (c – g – c).

Xét hai tam giác AOB và COD có:

OA = OC (theo giả thiết).

$\widehat{AOB}=\widehat{CO\text{D}}$ (2 góc đối đỉnh).

OB = OD (theo giả thiết).

Vậy $\Delta AOB=\Delta CO\text{D}$ (c – g – c).

b) Do $\Delta AO\text{D}=\Delta COB$ nên AD = BC (2 cạnh tương ứng).

Do $\Delta AOB=\Delta CO\text{D}$ nên AB = CD (2 cạnh tương ứng).

Xét hai tam giác DAB và BCD có:

AD = BC (chứng minh trên).

AB = CD (chứng minh trên).

BD chung.

Vậy $\Delta DAB=\Delta BC\text{D}$ (c – c – c).

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

Bài 4.14 trang 73 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Bài 4.14 trang 73 Toán 7 Tập 1: Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.

Lời giải:

Xét hai tam giác ADE và BCE có:

$\widehat{DA\text{E}}=\widehat{CBE}$ (theo giả thiết).

AE = BE (theo giả thiết).

$\widehat{A\text{ED}}=\widehat{BEC}$ (2 góc đối đỉnh).

Vậy $\Delta A\text{D}E=\Delta BCE$ (g – c – g).

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

Bài 4.15 trang 73 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Bài 4.15 trang 73 Toán 7 Tập 1: Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:

a) $\Delta ABE=\Delta DCE;$

b) EG = EH.

Lời giải:

a) Do AB // CD nên $\widehat{ABE}=\widehat{DCE}$ (2 góc so le trong) và $\widehat{BA\text{E}}=\widehat{C\text{D}E}$ (2 góc so le trong).

Xét hai tam giác ABE và DCE có:

$\widehat{ABE}=\widehat{DCE}$ (chứng minh trên).

AB = CD (theo giả thiết).

$\widehat{BA\text{E}}=\widehat{C\text{D}E}$ (chứng minh trên).

Vậy $\Delta ABE=\Delta DCE$ (g – c – g).

b) Do $\Delta ABE=\Delta DCE$ nên BE = CE (2 cạnh tương ứng).

Do G, E, H thẳng hàng $\widehat{GEB}=\widehat{HEC}$ (2 góc đối đỉnh).

Do $\widehat{ABE}=\widehat{DCE}$ nên $\widehat{GBE}=\widehat{HCE}.$

Xét hai tam giác GEB và HEC có:

$\widehat{GEB}=\widehat{HEC}$ (chứng minh trên).

BE = CE (chứng minh trên).

$\widehat{GBE}=\widehat{HCE}$ (chứng minh trên).

Do đó $\Delta GEB=\Delta HEC$ (g – c – g).

Vậy EG = EH (2 cạnh tương ứng).

Lời giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác hay khác:

Sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức

Với giải sách bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 14.

Giải SBT Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức

Giải SBT Toán 7 trang 60 Tập 1

Vở thực hành Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức

Với giải vở thực hành Toán lớp 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài 14.

Giải Vở thực hành Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Kết nối tri thức

B – Câu hỏi trắc nghiệm

Giải VTH Toán 7 trang 63 Tập 1

Trường hợp bằng nhau thứ hai và thứ ba của tam giác (Lý thuyết Toán lớp 7) - Kết nối tri thức

Với tóm tắt lý thuyết Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Trường hợp bằng nhau thứ hai và thứ ba của tam giác (Lý thuyết Toán lớp 7) - Kết nối tri thức

Lý thuyết Trường hợp bằng nhau thứ hai và thứ ba của tam giác

1. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)

• Trong tam giác ABC, góc BAC (hay góc A) được gọi là góc xen giữa của hai cạnh AB và AC.

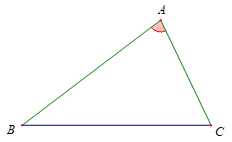
• Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

Ví dụ:

+ Tam giác ABC và tam giác EFD có cạnh AB = EF = 5cm; AC = ED = 3cm; góc A là góc xen giữa của cạnh AB và AC, góc E là góc xen giữa của cạnh EF và ED; $\hat{A}=\hat{E}=79°$.

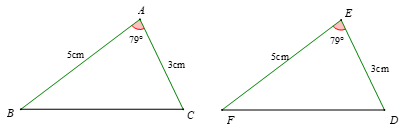
Khi đó ta có $\Delta ABC=\Delta EFD$ theo trường hợp cạnh góc cạnh (c.g.c)

2. Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (g.c.g)

• Trong tam giác ABC, hai góc ABC, ACB (hay góc B và góc C) được gọi là hai góc kề cạnh BC của tam giác ABC.

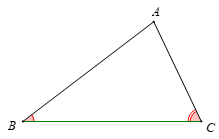
• Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Ví dụ

+ Tam giác ABC và tam giác EFD có $\hat{B}=\hat{F}=37°$; $\hat{C}=\hat{D}=64°$; góc B và góc C là hai góc kề của cạnh BC, góc F và góc D là hai góc kề của cạnh FD; cạnh BC = FD = 6cm.

Khi đóta có <$\Delta ABC=\Delta EFD$theo trường hợp góc cạnh góc (g.c.g)

Bài tập Trường hợp bằng nhau thứ hai và thứ ba của tam giác

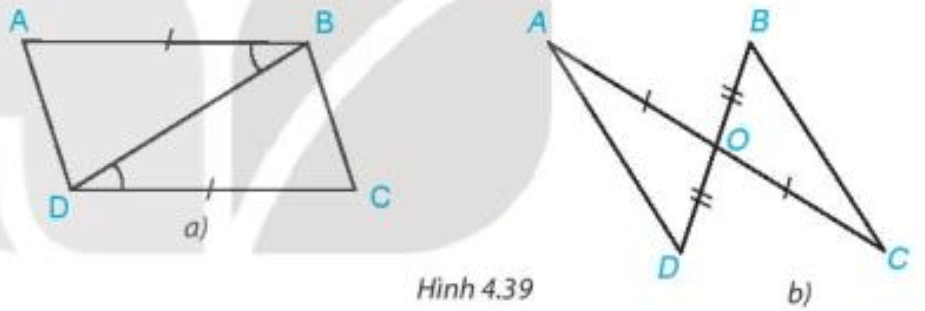
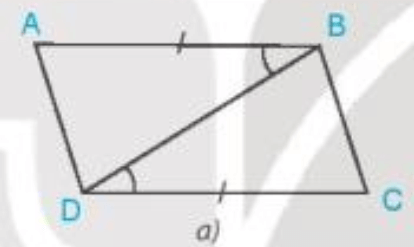
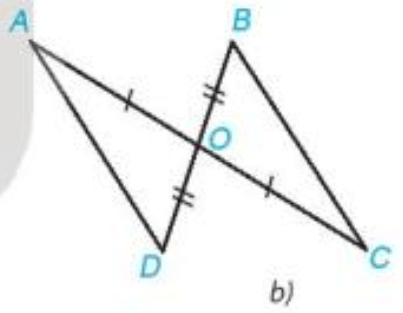
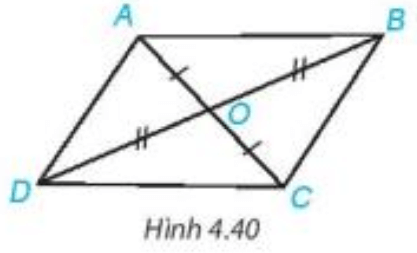
Bài 1. Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.

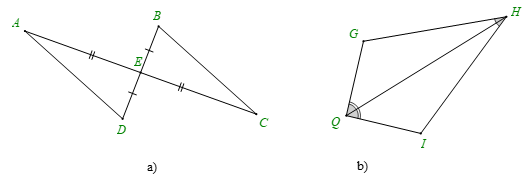
Hướng dẫn giải

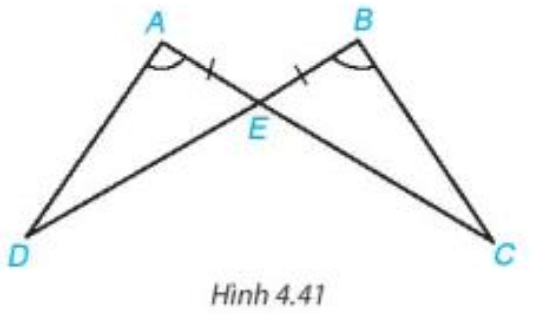
a) Hai tam giác AED và CEB có:

AE = CE

$\widehat{AED}=\widehat{CEB}$(hai góc đối đỉnh)

DE = BE

Do đó $\Delta AED=\Delta CEB$(c.g.c)

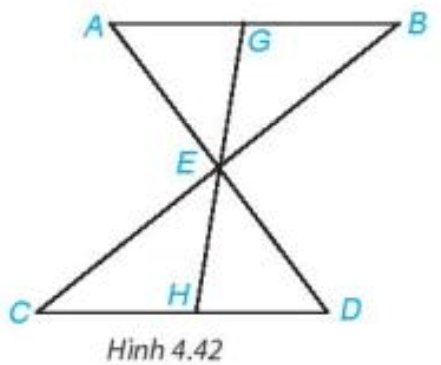
b) Hai tam giác QGH và QIH có:

$\widehat{GQH}=\widehat{IQH}$

QH là cạnh chung

$\widehat{GHQ}=\widehat{IHQ}$

Do đó $\Delta QGH=\Delta QIH$(g.c.g)

Bài 2. Cho hình vẽ dưới đây, biết CE = DE và $\widehat{CEA}=\widehat{DEA}$.

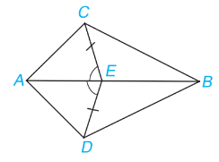
Chứng minh rằng:

a) $\Delta AEC=\Delta AED$;

b) $\Delta ABC=\Delta ABD$.

Hướng dẫn giải

a) Xét $\Delta AEC$ và $\Delta AED$ có:

CE = DE (theo giả thiết)

$\widehat{CEA}=\widehat{DEA}$ (theo giả thiết)

AE là cạnh chung

Do đó $\Delta AEC=\Delta AED$ (c.g.c)

b) Vì $\Delta AEC=\Delta AED$ (theo câu a)

⇒ AC = AD (2 cạnh tương ứng) và $\widehat{CAE}=\widehat{DAE}$ (2 góc tương ứng)

Xét $\Delta ABC$ và $\Delta ABD$ có:

AC = AD (chứng minh trên)

$\widehat{CAE}=\widehat{DAE}$ (chứng minh trên)

AB là cạnh chung

Do đó $\Delta ABC=\Delta ABD$ (c.g.c)

Bài 3. Cho hình vẽ dưới đây, biết đoạn thẳng JK song song và bằng đoạn thẳng ML.

Chứng minh rằng:

a) $\Delta JOK=\Delta LOM$

b) OP = OQ.

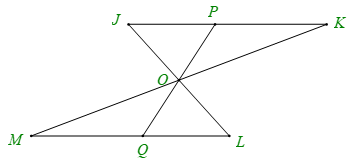
Hướng dẫn giải

a) Vì JK ∥ML nên:

$\widehat{\text{OJ}K}=\widehat{OLM}$ (2 góc so le trong)

$\widehat{\text{O}KJ}=\widehat{OML}$ (2 góc so le trong)

Xét $\Delta \text{JO}K$ và $\Delta LOM$ có:

$\widehat{\text{OJ}K}=\widehat{OLM}$ (chứng minh trên)

JK = ML (theo giả thiết)

$\widehat{\text{O}KJ}=\widehat{OML}$ (chứng minh trên)

Do đó $\Delta JOK=\Delta LOM$ (g.c.g)

b) Vì $\Delta JOK=\Delta LOM$ (theo câu a)

⇒ KO = MO (2 cạnh tương ứng)

Xét $\Delta KOP$ và $\Delta MOQ$ có:

$\widehat{\text{O}KJ}=\widehat{OML}$ (chứng minh trên)

KO = MO (chứng minh trên)

$\widehat{KOP}=\widehat{MOQ}$ (2 góc đối đỉnh)

Do đó $\Delta KOP=\Delta MOQ$ (g.c.g)

⇒ OP = OQ (2 cạnh tương ứng).

Học tốt Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Các bài học để học tốt Trường hợp bằng nhau thứ hai và thứ ba của tam giác Toán lớp 7 hay khác:

15 Bài tập Trường hợp bằng nhau thứ hai và thứ ba của tam giác (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Trường hợp bằng nhau thứ hai và thứ ba của tam giác (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Xem thử

Chỉ từ 150k mua trọn bộ trắc nghiệm Toán 7 Kết nối tri thức (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: