Tam giác cân. Đường trung trực của đoạn thẳng (Lý thuyết Toán lớp 7) - Kết nối tri thức
Với tóm tắt lý thuyết Toán 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng sách Kết nối tri thức hay nhất, chi tiết
sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.
Tam giác cân. Đường trung trực của đoạn thẳng (Lý thuyết Toán lớp 7) - Kết nối tri thức
Lý thuyết Tam giác cân. Đường trung trực của đoạn thẳng
1. Tam giác cân và tính chất
• Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.
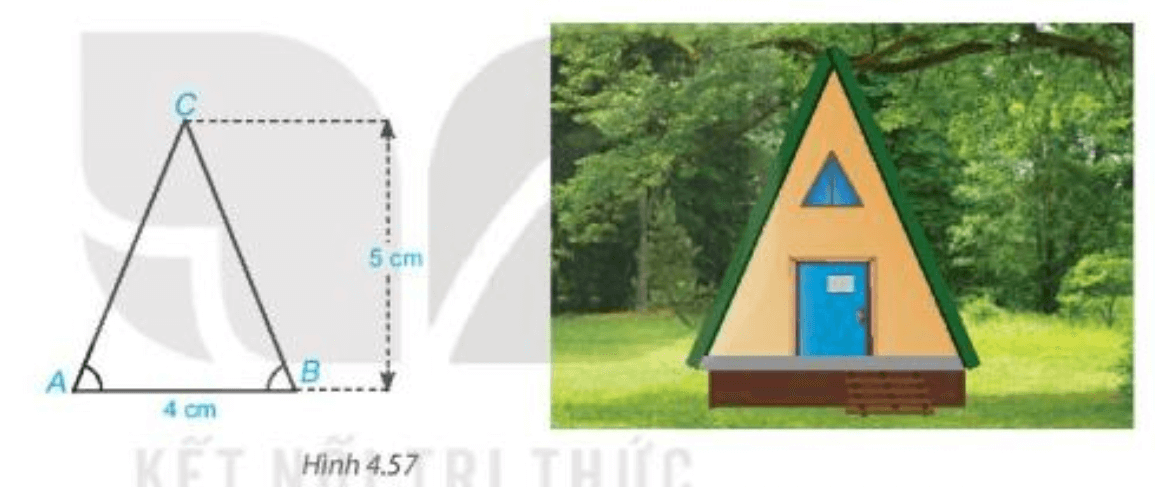
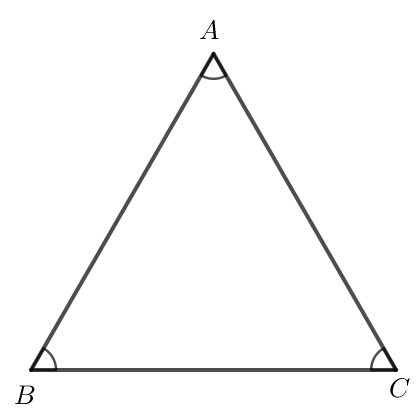
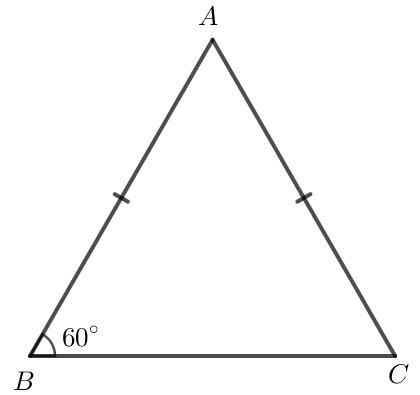
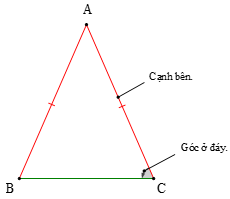
Ví dụ: Trong hình dưới đây, có cạnh AB = AC được gọi là tam giác cân tại đỉnh A, hai cạnh AB và AC là hai cạnh bên, BC là cạnh đáy, và là hai góc ở đáy, là góc ở đỉnh.
• Tính chất:
+ Trong tam giác cân, hai góc ở đáy bằng nhau.
+ Tam giác có hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân.
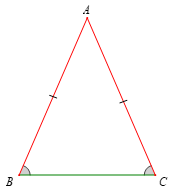
Ví dụ: Tam giác ABC cân tại A thì =. Ngược lại, tam giác ABC có =thì tam giác ABC cân tại A.
Chú ý:
• Tam giác đều là tam giác có ba cạnh bằng nhau. Khi đó ba góc cũng bằng nhau và bằng 60°.
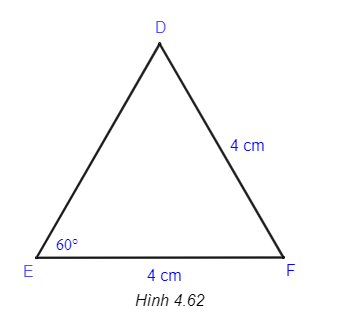
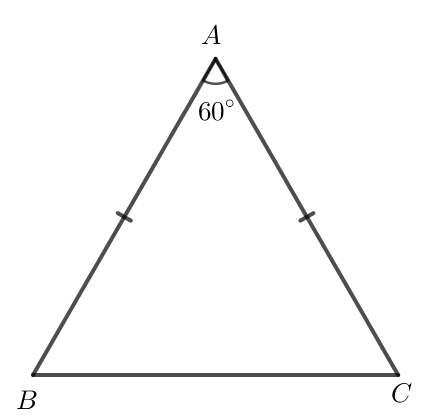
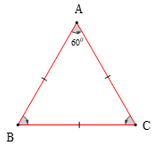
Ví dụ: Tam giác ABC có AB = AC = BC thì tam giác ABC được gọi là tam giác đều. Tam giác ABC đều có = == 60°.
• Một tam giác có ba cạnh hoặc ba góc bằng nhau thì tam giác ấy là tam giác đều.
• Tam giác cân có 1 góc bằng 60° thì tam giác ấy là tam giác đều.
2. Đường trung trực của một đoạn thẳng
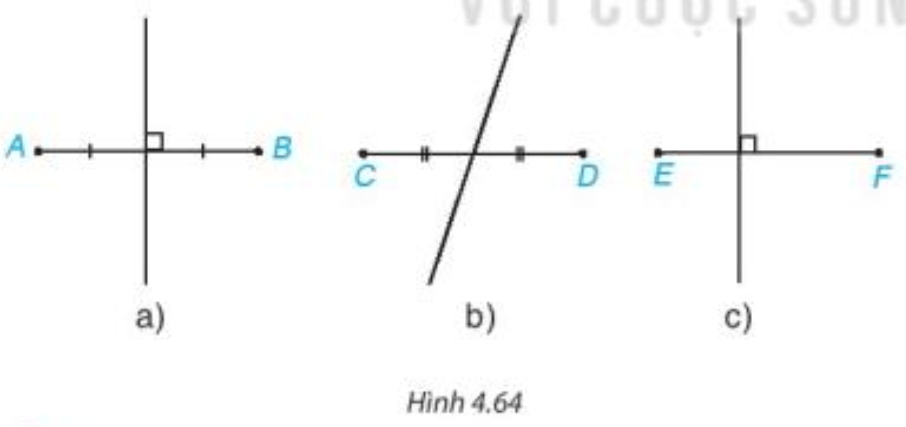
• Định nghĩa: Đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.
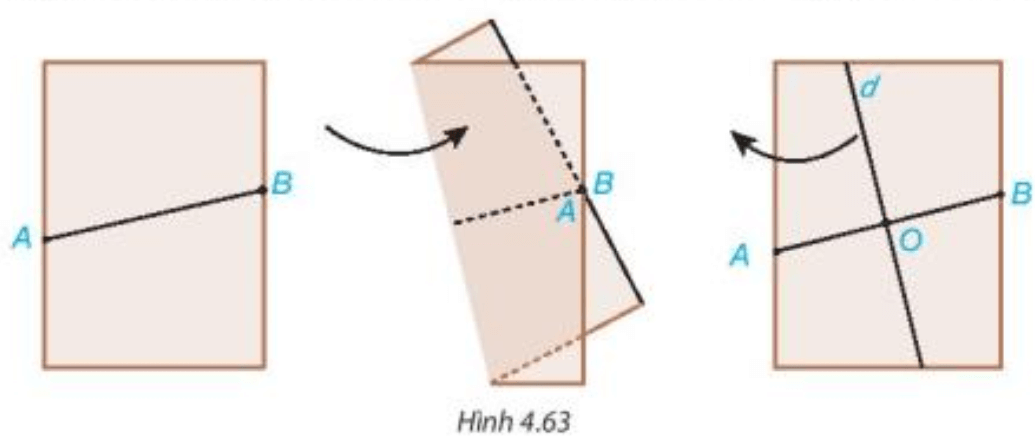
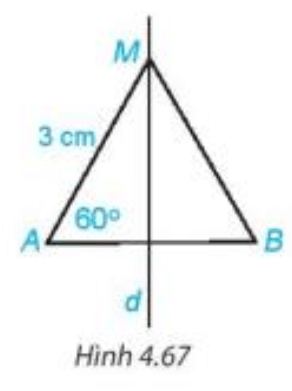
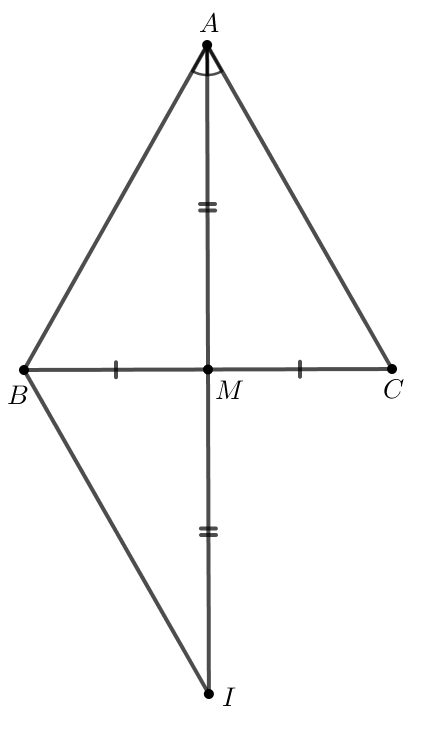
Ví dụ: Đường thẳng d vuông góc với đoạn AB tại M và M là trung điểm của AB. Khi đó d được gọi là đường trung trực của đoạn thẳng AB.
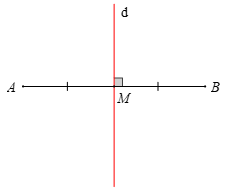
• Đường trung trực của đoạn thẳng cũng là trục đối xứng của đoạn thẳng đó.
• Tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
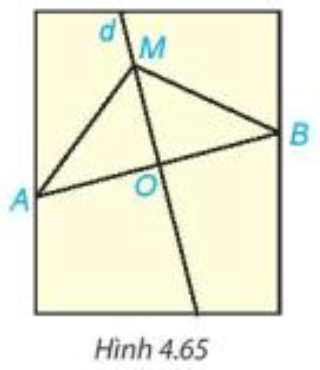
Ví dụ: Đường thẳng d là đường trung trực của đoạn thẳng AB và D ∈ d.
Khi đó DA = DB.
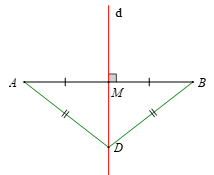
• Đường trung trực của đoạn thẳng là tập hợp tất cả các điểm cách đều hai mút của đoạn thẳng đó.
Chú ý:
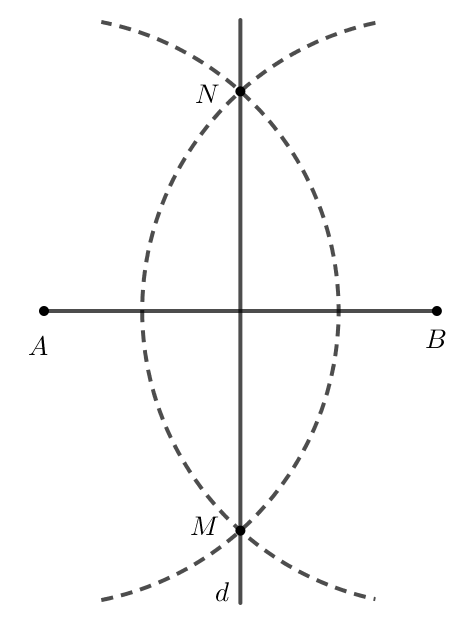
• Cách vẽ đường trung trực của đoạn thẳng bằng compa và thước thẳng.
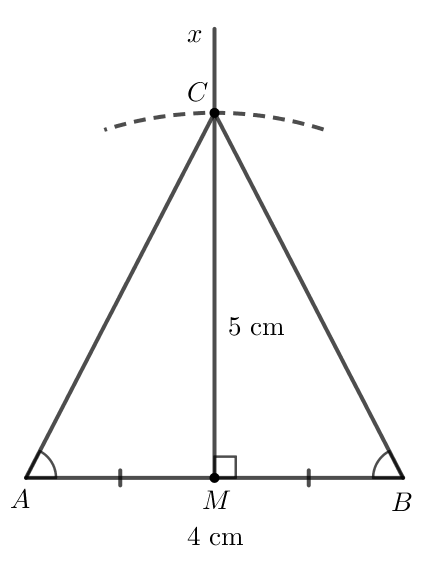
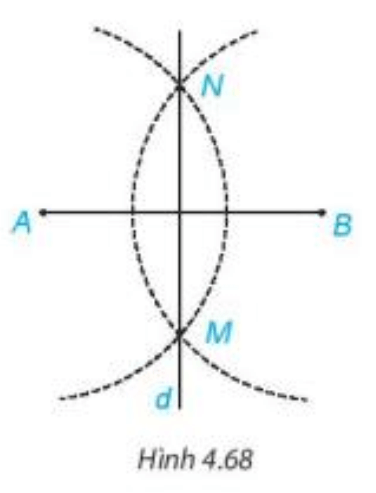
Chẳng hạn: Vẽ đường thẳng d là đường trung trực của đoạn thẳng AB như sau:
+ Vẽ đoạn thẳng AB;
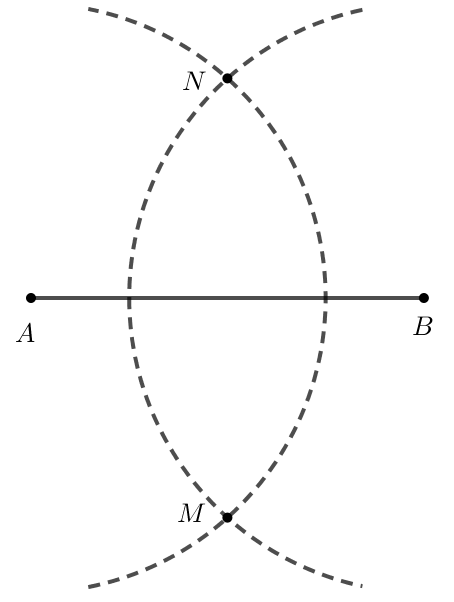
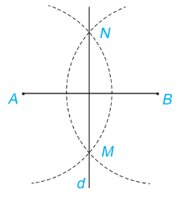
+ Lấy A làm tâm, vẽ cung tròn (bán kính lớn hơn ). Sau đó lấy B làm tâm, vẽ cung tròn cùng bán kính sao cho hai cung này cắt nhau tại hai điểm M và N;
+ Dùng thước thẳng vẽ đường thẳng đi qua M và N. Đường thẳng đó là đường trung trực của đoạn thẳng AB.
Bài tập Tam giác cân. Đường trung trực của đoạn thẳng
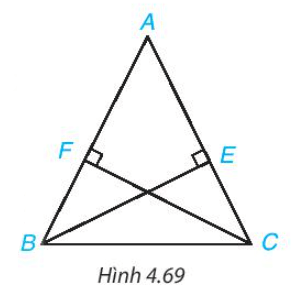
Bài 1. Cho tam giác ABC cân tại A. Kẻ BH và CK lần lượt vuông góc với AC và AB (H ∈ AC; K ∈ AB). Chứng minh rằng BH = CK.
Hướng dẫn giải


Xét tam giác BHA (vuông tại H) và tam giác CKA (vuông tại K) có:
AB = AC ( cân tại A)
là góc chung
⇒ (cạnh huyền – góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
Vậy BH = CK (đpcm).
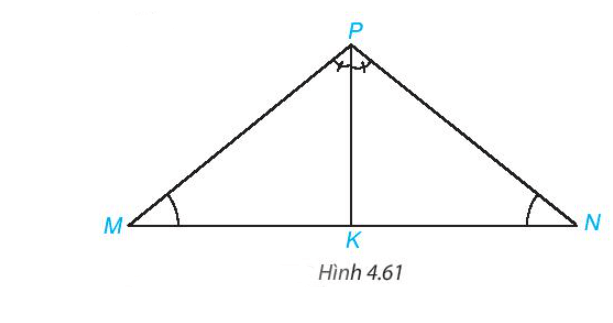
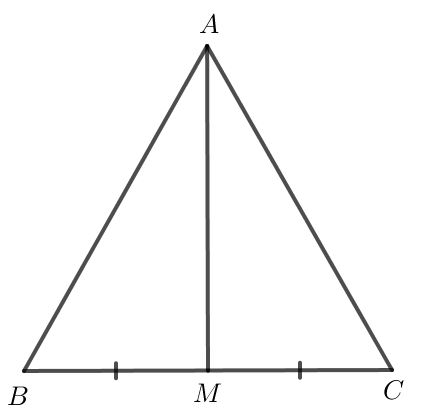
Bài 2. Cho tam giác ABC cân tại A. I là trung điểm của đoạn thẳng BC. Chứng minh AI vuông góc với BC và AI là tia phân giác của góc BAC.
Hướng dẫn giải

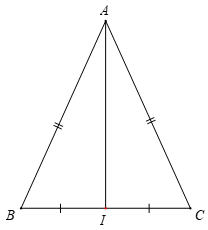
Xét tam giác AIB và tam giác AIC có:
AB = AC ( cân tại A)
BI = CI (theo giả thiết)
AI là cạnh chung
⇒ (c.c.c)
⇒ (hai góc tương ứng)
Mà
⇒
⇒ AI ⊥ BC (đpcm)
Vì (chứng minh trên)
⇒ (hai góc tương ứng)
⇒ AI là tia phân giác của góc BAC (đpcm).
Bài 3. Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh tam giác ADE là tam giác cân.
Hướng dẫn giải
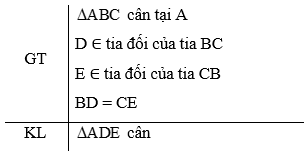
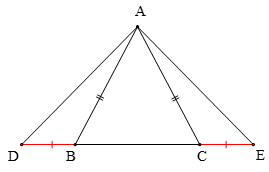
cân tại A ⇒ (tính chất)
Mà: (hai góc kề bù)
(hai góc kề bù)
Do đó,
Xét tam giác ADB và tam giác AEC có:
AB = AC ( cân tại A)
(chứng minh trên)
BD = CE (theo giả thiết)
⇒ (c.g.c)
⇒ AD = AE (hai cạnh tương ứng)
⇒ cân tại A (đpcm).
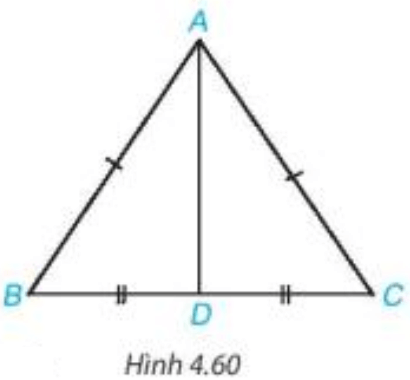
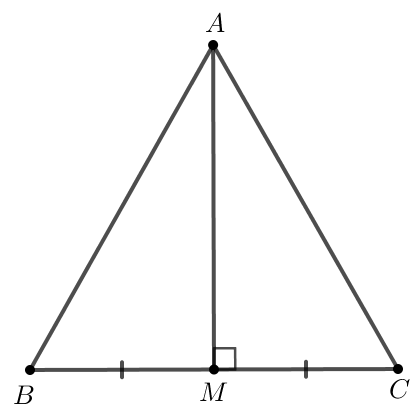
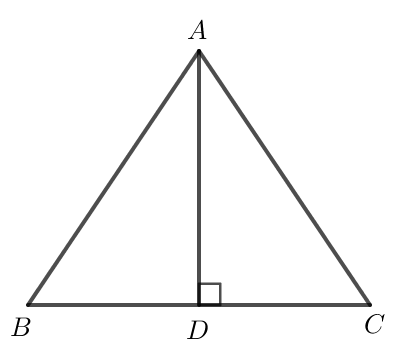
Bài 4. Cho tam giác ABC cân tại A có AH là đường phân giác của góc BAC (H ∈ BC). Chứng minh AH là đường trung trực của đoạn thẳng BC.
Hướng dẫn giải

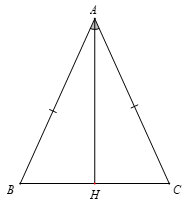
Xét tam giác ABH và tam giác ACH có:
AB = AC ( cân tại A)
(AH là đường phân giác của )
AH là cạnh chung
⇒ (c.g.c)
⇒ HB = HC (hai cạnh tương ứng) (1)
Và (hai góc tương ứng)
Mà (hai góc kề bù)
⇒ ⇒ AH ⊥ BC (2)
Từ (1) và (2) ⇒AH là đường trung trực của đoạn thẳng BC (đpcm).
Học tốt Tam giác cân. Đường trung trực của đoạn thẳng
Các bài học để học tốt Tam giác cân. Đường trung trực của đoạn thẳng Toán lớp 7 hay khác: