Với giải bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán 7 Bài 30.

Giải Toán 7 Kết nối tri thức Bài 30: Làm quen với xác suất của biến cố

1. Xác suất của biến cố

Giải Toán 7 trang 51 Tập 2

HĐ1 trang 51 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 30: Làm quen với xác suất của biến cố

HĐ1 trang 51 Toán 7 Tập 2: Chọn cụm từ thích hợp (không thể, ít khả năng, nhiều khả năng, chắc chắn) thay vào dấu “?” trong các câu sau:

a) Tôi ..?.. đi bộ 20 km mà không nghỉ.

b) ..?.. có tuyết rơi ở Hà Nội vào mùa đông.

c) Anh An là một học sinh giỏi. Anh An ..?.. sẽ đỗ thủ khoa trong kì thi Trung học phổ thông quốc gia tới.

Lời giải:

a) Tôi không thể đi bộ 20 km mà không nghỉ.

b) Ít khả năng có tuyết rơi ở Hà Nội vào mùa đông.

c) Anh An là một học sinh giỏi. Anh An nhiều khả năng sẽ đỗ thủ khoa trong kì thi Trung học phổ thông quốc gia tới.

Lời giải bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố hay, chi tiết khác:

HĐ2 trang 51 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 30: Làm quen với xác suất của biến cố

HĐ2 trang 51 Toán 7 Tập 2: Một hộp đựng 20 viên bi, trong đó 13 viên màu đỏ và 7 viên màu đen có cùng kích thước. Ban Nam lấy ngẫu nhiên một viên bi từ trong hộp. Hỏi khả năng Nam lấy được viên bi màu nào lớn hơn?

Lời giải:

Do số bi đỏ nhiều hơn số bi đen nên khả năng Nam lấy được viên bi màu đỏ lớn hơn.

Lời giải bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố hay, chi tiết khác:

Luyện tập 1 trang 52 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 30: Làm quen với xác suất của biến cố

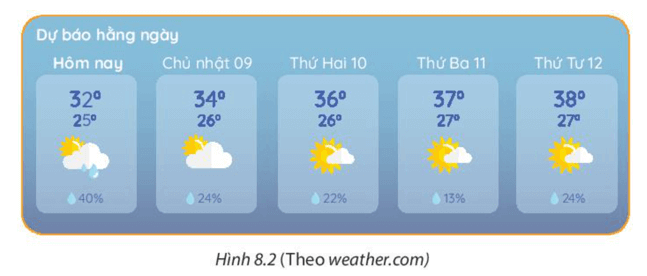
Luyện tập 1 trang 52 Toán 7 Tập 2: Hình 8.2 cho biết thông tin dự báo thời tiết tại thành phố Hà Nội trong 5 ngày

(từ 8 - 5 - 2021 đến 12 - 5 - 2021).

Quan sát hình trên, em hãy cho biết ngày nào có khả năng (hay xác suất) mưa nhiều nhất, ít nhất.

Lời giải:

Ngày có khả năng mưa nhiều nhất là ngày 8 - 5 - 2021.

Ngày có khả năng mưa ít nhất là ngày 11 - 5 - 2021.

Lời giải bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố hay, chi tiết khác:

Luyện tập 2 trang 53 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 30: Làm quen với xác suất của biến cố

Luyện tập 2 trang 53 Toán 7 Tập 2: Gieo đồng thời hai con xúc xắc. Tìm xác suất của các biến cố sau:

- Tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn 13.

- Tổng số chấm xuất hiện trên hai con xúc xắc bằng 1.

Lời giải:

Số chấm cao nhất xuất hiện trong các mặt của con xúc xắc là 6, do đó tổng số chấm xuất hiện trên hai con xúc xắc cao nhất là 12.

Do đó biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn 13” là biến cố chắc chắn nên xác suất của biến cố này bằng 1.

Số chấm thấp nhất xuất hiện trong các mặt của con xúc xắc là 1, do đó tổng số chấm xuất hiện trên hai con xúc xắc luôn lớn hơn 1.

Do đó biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 1” là biến cố không thể nên xác suất của biến cố này bằng 0.

Lời giải bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố hay, chi tiết khác:

Luyện tập 3 trang 54 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 30: Làm quen với xác suất của biến cố

Luyện tập 3 trang 54 Toán 7 Tập 2: Trong trò chơi Ô cửa bí mật, có ba ô cửa 1, 2, 3 và người ta đặt phần thưởng sau một ô cửa. Người chơi sẽ chọn ngẫu nhiên một ô cửa trong ba ô cửa và nhận phần thưởng sau ô cửa đó. Tìm xác suất để người chơi chọn được ô cửa có phần thưởng.

Lời giải:

Do có ba ô cửa và chỉ có 1 ô cửa có phần thưởng nên xuất suất để người chơi chọn được ô cửa có phần thưởng là $\frac{1}{3}$

Lời giải bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố hay, chi tiết khác:

Luyện tập 4 trang 54 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 30: Làm quen với xác suất của biến cố

Luyện tập 4 trang 54 Toán 7 Tập 2: Gieo một con xúc xắc được chế tạo cân đối.

Tìm xác suất để số chấm xuất hiện trên con xúc xắc là 2.

Lời giải:

Một con xúc xắc có 6 mặt có số chấm từ 1 đến 6.

Do đó xác suất để xuất hiện mặt 2 chấm là $\frac{1}{6}$.

Lời giải bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố hay, chi tiết khác:

Bài 8.4 trang 55 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 30: Làm quen với xác suất của biến cố

Bài 8.4 trang 55 Toán 7 Tập 2: Mai và Việt mỗi người gieo một con xúc xắc. Tìm xác suất của các biến cố sau:

a) Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 1;

b) Tích số chấm xuất hiện trên hai con xúc xắc lớn hơn 36.

Lời giải:

a) Số chấm thấp nhất xuất hiện trong các mặt của con xúc xắc là 1, do đó tổng số chấm xuất hiện trên hai con xúc xắc luôn lớn hơn 1.

Do đó biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 1” là biến cố chắc chắn nên xác suất của biến cố này bằng 1.

b) Số chấm cao nhất xuất hiện trong các mặt của con xúc xắc là 6, do đó tích số chấm xuất hiện trên hai con xúc xắc cao nhất là 36.

Do đó biến cố “Tích số chấm xuất hiện trên hai con xúc xắc lớn hơn 36” là biến cố không thể nên xác suất của biến cố này bằng 0.

Lời giải bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố hay, chi tiết khác:

Bài 8.5 trang 55 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 30: Làm quen với xác suất của biến cố

Bài 8.5 trang 55 Toán 7 Tập 2: Trước trận chung kết bóng đá World Cup năm 2010 giữa hai đội Hà Lan và Tây Ban Nha, để dự đoán kết quả người ta bỏ cùng loại thức ăn vào hai hộp giống nhau, một hộp có gắn cờ Hà Lan, một hộp gắn cờ Tây Ban Nha và cho Paul chọn hộp thức ăn. Người ta cho rằng nếu Paul chọn hộp gắn cờ nước nào thì đội bóng của nước đó thắng. Paul chọn ngẫu nhiên một hộp. Tính xác suất để Paul dự đoán đội Tây Ban Nha thắng.

Lời giải:

Paul chọn ngẫu nhiên một hộp trong hai hộp thức ăn nên xác suất để Paul dự đoán đội Tây Ban Nha thắng là $\frac{1}{2}$.

Lời giải bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố hay, chi tiết khác:

Bài 8.6 trang 55 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 30: Làm quen với xác suất của biến cố

Bài 8.6 trang 55 Toán 7 Tập 2: Một tổ học sinh của lớp 7B có 5 bạn nam và 5 bạn nữ. Giáo viên gọi ngẫu nhiên một bạn lên bảng để kiểm tra bài tập. Xét hai biến cố sau:

A: “Bạn được gọi là bạn nam” và B: “Bạn được gọi là bạn nữ”.

a) Hai biến cố A và B có đồng khả năng không? Vì sao?

b) Tìm xác suất của biến cố A và biến cố B.

Lời giải:

a) Do số bạn nam và số bạn nữ trong tổ đó bằng nhau nên biến cố A và biến cố B đồng khả năng.

b) Do biến cố A và biến cố B đồng khả năng nên xác suất của biến cố A bằng xác suất của biến cố B và bằng $\frac{1}{2}$.

Lời giải bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố hay, chi tiết khác:

Bài 8.7 trang 55 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 30: Làm quen với xác suất của biến cố

Bài 8.7 trang 55 Toán 7 Tập 2: Gieo một con xúc xắc được chế tạo cân đối. Tìm xác suất của các biến cố sau:

A: “Số chấm xuất hiện trên con xúc xắc nhỏ hơn 7”;

B: “Số chấm xuất hiện trên con xúc xắc là 0”;

C: “Số chấm xuất hiện trên con xúc xắc là 6”.

Lời giải:

Số chấm cao nhất xuất hiện trong các mặt của con xúc xắc là 6, do đó biến cố A là biến cố chắc chắn nên xác suất của biến cố A bằng 1.

Số chấm thấp nhất xuất hiện trong các mặt của con xúc xắc là 1, do đó biến cố B là biến cố không thể nên xác suất của biến cố B bằng 0.

Một con xúc xắc có 6 mặt có số chấm từ 1 đến 6.

Do đó xác suất để xuất hiện mặt 6 chấm là $\frac{1}{6}$hay xác suất của biến cố C bằng $\frac{1}{6}$.

Luyện tập chung

Lời giải bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố hay, chi tiết khác:

Sách bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố - Kết nối tri thức

Với giải sách bài tập Toán 7 Bài 30: Làm quen với xác suất của biến cố sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 30.

Giải SBT Toán 7 Bài 30: Làm quen với xác suất của biến cố - Kết nối tri thức

Giải SBT Toán 7 trang 43 Tập 2

Vở thực hành Toán 7 Bài 30: Làm quen với xác suất của biến cố - Kết nối tri thức

Với giải vở thực hành Toán lớp 7 Bài 30: Làm quen với xác suất của biến cố sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài 30.

Giải vở thực hành Toán 7 Bài 30: Làm quen với xác suất của biến cố - Kết nối tri thức

Giải VTH Toán 7 trang 59 Tập 2

Làm quen với xác suất của biến cố (Lý thuyết Toán lớp 7) - Kết nối tri thức

Với tóm tắt lý thuyết Toán 7 Bài 30: Làm quen với xác suất của biến cố sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Làm quen với xác suất của biến cố (Lý thuyết Toán lớp 7) - Kết nối tri thức

Lý thuyết Làm quen với xác suất của biến cố

1. Xác suất của biến cố

Khả năng xảy ra của một biến cố được đo lường bởi một số nhận giá trị từ 0 đến 1, gọi là xác suất của biến cố đó.

Nhận xét: Xác suất của một biến cố càng gần 1 thì biến cố đó càng có nhiều khả năng xảy ra. Xác suất của một biến cố càng gần 0 thì biến cố đó càng ít khả năng xảy ra.

Ví dụ: Lớp 7A tổ chức trò chơi và chia lớp thành 2 nhóm: Nhóm I và nhóm II. Theo dự đoán của các bạn trong lớp, xác suất để nhóm I giành chiến thắng là 45%, xác suất thua là 40% và xác suất hòa là 15%. Theo dự đoán trên, nhóm nào có khả năng giành chiến thắng cao hơn?

Hướng dẫn giải:

Xác suất thua của nhóm I là 40%, tức là xác suất thắng của nhóm II là 40%.

Do đó xác suất thắng của nhóm I lớn hơn xác suất thắng của nhóm II.

Vậy nhóm I có khả năng thắng cao hơn.

2. Xác suất của một số biến cố đơn giản

a. Xác suất của biến cố chắc chắn, biến cố không thể

Khả năng xảy ra của biến cố chắc chắn là 100%. Vậy biến cố chắc chắn có xác suất bằng 1.

Khả năng xảy ra của biến cố không thể là 0%. Vậy biến cố không thể có xác suất bằng 0.

Ví dụ 1:

Xác xuất của biến cố A: “Chúng ta có thể quay về quá khứ” bằng 0 vì A là biến cố không thể.

Xác suất của biến cố B: “Ngày mai Mặt Trời mọc ở đằng đông” bằng 1 vì B là biến cố chắc chắn.

Xét hai biến cố A và B, nếu chỉ xảy ra hoặc A hoặc B và hai biến cố A, B là đồng khả năng thì xác suất của chúng bằng nhau và bằng 0,5.

Ví dụ 2:Bạn An tung một đồng xu cân đối và đồng chất. Tìm xác suất của biến cố sau: “Tung được mặt ngửa”.

Hướng dẫn giải:

Khi tung một đồng xu thì có thể xảy ra khả năng đồng xu xuất hiện mặt sấp hoặc đồng xu xuất hiện mặt ngửa. Vì là đồng xu cân đối và đồng chất nên việc tung được mặt sấp hoặc mặt ngửa đều có khả năng xảy ra là bằng nhau.

Do đó xác suất xảy ra biến cố bằng 0,5.

b. Xác suất của các biến cố đồng khả năng

∙ Gieo một đồng xu cân đối. Xét hai biến cố sau:

A: “Đồng xu xuất hiện mặt ngửa”.

B: “Đồng xu xuất hiện mặt sấp”.

Do đồng xu cân đối nên biến cố A và biến cố B có khả năng xảy ra như nhau. Ta nói hai biến cố A và B là đồng khả năng.

Vì chỉ xảy ra hoặc biến cố A hoặc biến cố B nên xác suất của biến cố A và xác suất của biến cố B bằng nhau và bằng $\frac{1}{2}$ (hay 50%).

Ví dụ: Khi gieo một đồng xu cân đối, xác suất xuất hiện mặt sấp và mặt ngửa bằng nhau và đều bằng $\frac{1}{2}$.

∙ Trong một trò chơi hay thí nghiệm, nếu có k biến cố đồng khả năng và luôn xảy ra duy nhất một biến cố trong k biến cố này thì xác suất của mỗi biến cố đó đều bằng $\frac{1}{k}$.

Ví dụ:Gieo một con xúc xắc được chế tạo cân đối. Tính xác suất của biến cố sau:

A: “Số chấm xuất hiện trên mặt con xúc xắc là 6”.

Hướng dẫn giải:

Khi gieo một con xúc xắc cân đối thì 6 mặt của nó có khả năng xuất hiện bằng nhau nên xác suất xuất hiện của mỗi mặt đều là $\frac{1}{6}$.

Do 6 kết quả đều có khả năng xảy ra bằng nhau nên xác suất của biến cố đã cho bằng $\frac{1}{6}$.

Bài tập Làm quen với xác suất của biến cố

Bài 1.Một chiếc hộp đựng 6 chiếc thẻ ghi các số 5; 6; 7; 8; 9; 11. Rút ngẫu nhiên một tấm thẻ trong hộp. Tính xác suất để:

a) Rút được tấm thẻ ghi số nhỏ hơn 12;

b) Rút được tấm thẻ ghi số 10;

c) Rút được tấm thẻ ghi số 7.

Hướng dẫn giải

a) Biến cố: “Rút được tấm thẻ ghi số nhỏ hơn 12” là biến cố chắc chắn vì trong hộp cả 6 tấm thẻ đều ghi số nhỏ hơn 12.

Vậy xác suất của biến cố này bằng 1.

b) Biến cố: “Rút được tấm thẻ ghi số 10” là biến cố không thể vì trong hộp không có tấm thẻ nào ghi số 10.

Vậy xác suất của biến cố này bằng 0.

c) Do rút ngẫu nhiên nên mỗi tấm thẻ có khả năng rút được như nhau.

Trong hộp có sáu tấm thẻ nên có sáu biến cố đồng khả năng.

Vì luôn xảy ra duy nhất một trong sáu biến cố đó nên xác suất để rút được tấm thẻ ghi số 7 là $\frac{1}{6}$.

Bài 2.Lớp 7A có 40 học sinh trong đó có 10 học sinh nam. Giáo viên gọi ngẫu nhiên một bạn lên bảng để kiểm tra bài tập. Hỏi bạn nam hay bạn nữ có khả năng được gọi lên bảng nhiều hơn? Tại sao?

Hướng dẫn giải

Bạn nữ có khả năng được gọi lên bảng nhiều hơn vì lớp 7A có nhiều học sinh nữ hơn nên xác suất để bạn nữ được gọi lên bảng lớn hơn.

Bài 3.Trong một ống cắm bút có 1 bút vàng, 1 bút đỏ và 1 bút đen có kích thước và khối lượng như nhau. Lần lượt lấy ra 1 bút từ ống. Gọi A là biến cố: ''Lấy được bút đỏ ở lần thứ nhất''. Tìmxác suất của biến cố đã cho.

Hướng dẫn giải

Trong hoạt động trên có 3 kết quả có thể xảy ra đó là ở lần lấy thứ nhất có thể lấy ra bút vàng hoặc bút đỏ hoặc bút đen.

Vì các bút có kích thước và khối lượng như nhau nên mỗi kết quả đều có khả năng xảy ra bằng nhau do đó xác suất của biến cố đã cho bằng $\frac{1}{3}$.

Bài 4.Một hộp đựng 20 quả bóng có cùng kích thước, khác nhau về màu sắc trong đó có 5 quả bóng màu xanh, 5 quả bóng màu đỏ, 5 quả bóng màu đen, 5 quả bóng màu vàng. Bạn An lấy ngẫu nhiên 1 quả bóng từ trong hộp.

Xét 4 biến cố sau:

A: “Minh lấy được quả bóng màu xanh”;

B: “Minh lấy được quả bóng màu đỏ”;

C: “Minh lấy được quả bóng màu đen”;

D: “Minh lấy được quả bóng màu vàng”.

Tính xác suất của các biến cố A, B, C, D.

Hướng dẫn giải

Mỗi quả bóng có khả năng được chọn như nhau.

Số quả bóng màu xanh, màu đỏ, màu đen, màu vàng bằng nhau nên các biến cố A, B, C, D là đồng khả năng.

Vì luôn xảy ra duy nhất một trong 4 biến cố này nên xác suất của bốn biến cố bằng nhau và bằng $\frac{1}{4}$.

Học tốt Làm quen với xác suất của biến cố

Các bài học để học tốt Làm quen với xác suất của biến cố Toán lớp 7 hay khác:

15 Bài tập Làm quen với xác suất của biến cố (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Làm quen với xác suất của biến cố Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Làm quen với xác suất của biến cố (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Xem thử

Chỉ 150k mua trọn bộ trắc nghiệm Toán 7 Kết nối tri thức (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: