Giải Toán 7 | No tags
Với giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán Hình 7 Bài 35.
Mở đầu
Mở đầu trang 77 Toán 7 Tập 2: Có thể coi ba ngôi nhà của ba anh em trong một khu vườn là ba đỉnh của một tam giác (không tù). Họ muốn khoan một giếng chung trong vườn cách đều ba ngôi nhà (H.9.36). Em có thể giúp họ chọn địa điểm để khoan giếng không?
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Lời giải:
Coi ba ngôi nhà của ba anh em là ba đỉnh của tam giác.
Khi đó đường thẳng nối 2 trong 3 nhà với nhau là cạnh của tam giác.
Giếng cách đều 3 ngôi nhà tức giếng cách đều 3 đỉnh của tam giác.
Khi đó giếng là giao điểm ba đường trung trực của tam giác.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Câu hỏi trang 77 Toán 7 Tập 2: Mỗi tam giác có mấy đường trung trực?
Lời giải:
Một tam giác có 3 cạnh nên mỗi tam giác sẽ có 3 đường trung trực tương ứng với mỗi cạnh.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
HĐ1 trang 78 Toán 7 Tập 2: Vẽ tam giác ABC (không tù) và ba đường trung trực của các đoạn thẳng BC, CA, AB. Quan sát hình và cho biết ba đường trung trực đó có cùng đi qua một điểm không.
Lời giải:
Ta thấy ba đường trung trực của tam giác cùng đi qua một điểm.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
HĐ2 trang 78 Toán 7 Tập 2: Dùng tính chất đường trung trực của một đoạn thẳng, hãy lập luận để suy ra tính chất nói ở HĐ1 bằng cách trả lời các câu hỏi sau:
Cho O là giao điểm các đường trung trực của hai cạnh BC và CA (H.9.38).
a) Tại sao OB = OC, OC = OA?
b) Điểm O có nằm trên đường trung trực của cạnh AB không?
Lời giải:
a) Do O nằm trên đường trung trực của cạnh BC nên OB = OC.
Do O nằm trên đường trung trực của cạnh CA nên OC = OA.
b) Do OB = OC và OC = OA nên OA = OB.
Do đó O nằm trên đường trung trực của cạnh AB.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Luyện tập 1 trang 79 Toán 7 Tập 2: Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều ba đỉnh của tam giác đó.
Lời giải:
Gọi M là giao điểm của BG và AC, N là giao điểm của CG và AB.
Do ∆ABC đều nên AB = BC = CA và.
M là trung điểm của AC nên AM = MC.
Xét ∆ABM và ∆CBM có:
AB = CB (chứng minh trên).
(chứng minh trên).
AM = CM (chứng minh trên).
Suy ra ∆ABM = ∆CBM (c - g - c).
Do đó (2 góc tương ứng).
Mà nên .
Do đó BM ⊥ AC.
BM vuông góc với AC tại trung điểm M của AC nên BM là đường trung trực của AC.
N là trung điểm của AB nên AN = BN.
Xét ∆CAN và ∆CBN có:
CA = CB (chứng minh trên).
(chứng minh trên).
AN = BN (chứng minh trên).
Suy ra ∆CAN = ∆CBN (c - g - c).
Do đó (2 góc tương ứng).
Mà nên .
Do đó CN ⊥ AB.
CN vuông góc với AB tại trung điểm N của AB nên CN là đường trung trực của AB.
G là giao điểm 2 đường trung trực của ∆ABC nên G cách đều 3 đỉnh của tam giác.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Vận dụng 1 trang 79 Toán 7 Tập 2: Em hãy trả lời câu hỏi trong tình huống mở đầu.
Lời giải:
Coi ba ngôi nhà của ba anh em là ba đỉnh của tam giác.
Khi đó đường thẳng nối 2 trong 3 nhà với nhau là cạnh của tam giác.
Giếng cách đều 3 ngôi nhà tức giếng cách đều 3 đỉnh của tam giác.
Khi đó giếng là giao điểm ba đường trung trực của tam giác.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Thử thách nhỏ trang 79 Toán 7 Tập 2: Sử dụng tính chất đường trung trực của một đoạn thẳng, hãy giải thích nếu điểm Q cách đều ba đỉnh của tam giác ABC thì Q phải là giao điểm ba đường trung trực của tam giác ABC.
Lời giải:
Q cách đều 3 đỉnh của tam giác ABC nên QA = QB = QC.
Do QA = QB nên Q nằm trên đường trung trực của AB.
Do QB = QC nên Q nằm trên đường trung trực của BC.
Do QC = QA nên Q nằm trên đường trung trực của CA.
Do đó Q là giao điểm ba đường trung trực của tam giác ABC.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Câu hỏi trang 79 Toán 7 Tập 2: Mỗi tam giác có mấy đường cao?
Lời giải:
Mỗi tam giác có 3 đường cao xuất phát từ 3 đỉnh của tam giác.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
HĐ3 trang 79 Toán 7 Tập 2: Vẽ tam giác ABC và ba đường cao của nó. Quan sát hình và cho biết, ba đường cao đó có cùng đi qua một điểm không.
Lời giải:
Ta thấy ba đường cao của tam giác cùng đi qua một điểm.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Luyện tập 2 trang 81 Toán 7 Tập 2:
a) Chứng minh rằng trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Lời giải:
a)
Gọi M là trung điểm của BC.
Do tam giác ABC cân tại A nên AB = AC và .
Do AB = AC nên A nằm trên đường trung trực của BC.
Do đó AM ⊥ BC nên AM là đường cao của tam giác ABC.
Xét ∆ABM có = 90o (trong tam giác vuông, hai góc nhọn phụ nhau).
Suy ra (1).
Xét ∆ACM có = 90o (trong tam giác vuông, hai góc nhọn phụ nhau).
Suy ra (2).
Mà nên từ (1) và (2) ta có .
Do đó AM là tia phân giác của .
Vậy đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác ABC.
b)
Trong tam giác ABC đều có điểm O là điểm cách đều 3 đỉnh của tam giác.
Gọi M, N, P lần lượt là trung điểm của AB, AC, BC.
Do O cách đều 3 đỉnh của tam giác ABC nên O là giao điểm 3 đường trung trực của tam giác ABC.
Do đó OM ⊥ AM, ON ⊥ AN, OP ⊥ CP.
∆ABC đều nên AB = AC = BC.
Do M, N, P lần lượt là trung điểm của AB, AC, BC nên AM = AN = NC = CP.
Xét ∆OAM vuông tại M và ∆OAN vuông tại N:
AM = AN (chứng minh trên).
OA chung.
Suy ra ∆OAM = ∆OAN (cạnh huyền - cạnh góc vuông).
Do đó OM = ON (2 cạnh tương ứng) (2).
Xét ∆OCN vuông tại N và ∆OCP vuông tại P:
CN = CP (chứng minh trên).
OC chung.
Suy ra ∆OCN = ∆OCP (cạnh huyền - cạnh góc vuông).
Do đó ON = OP (2 cạnh tương ứng) (2).
Từ (1) và (2) suy ra OM = ON = OP.
Vậy trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Bài 9.26 trang 81 Toán 7 Tập 2: Gọi H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HBC, HCA, HAB.
Lời giải:
Gọi D, E, F lần lượt là chân đường cao kẻ từ A, B, C đến BC, CA, AB.
Xét ∆HBC có HD ⊥ BC, BF ⊥ HC.
HD cắt BF tại A nên A là trực tâm của ∆HCA.
Xét ∆HCA có HE ⊥ AC, BF ⊥ HC.
HE cắt BF tại B nên B là trực tâm của ∆HCA.
Xét ∆HAB có HF ⊥ AB, AE ⊥ HB.
HF cắt AE tại C nên C là trực tâm của ∆HAB.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Bài 9.27 trang 81 Toán 7 Tập 2: Cho tam giác ABC có = 100o và trực tâm H. Tính góc BHC.
Lời giải:
Gọi D, F, E lần lượt là chân đường cao kẻ từ A, B, C đến BC, CA, AB.
Ta có (2 góc đối đỉnh), (2 góc đối đỉnh).
Do đó = 100o.
Xét ∆FAH vuông tại F: = 90o (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó .
Xét ∆EAH vuông tại E: = 90o (trong tam giác vuông, hai góc nhọn phụ nhau).
Do đó .
Khi đó
hay .
Do đó = 180o – 100o = 80o.
Vậy = 80o.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Bài 9.28 trang 81 Toán 7 Tập 2: Xét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.
Lời giải:
Giả sử O nằm trên cạnh BC.
Do OA = OB nên ∆OAB cân tại O.
Do đó .
Do OA = OC nên ∆OAC cân tại O.
Do đó .
Khi đó hay .
Xét ∆ABC có .
Mà nên hay .
Do đó ∆ABC vuông tại A.
Vậy nếu O nằm trên một cạnh của tam giác ABC và O cách đều ba đỉnh của tam giác ABC thì ABC là một tam giác vuông.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Bài 9.29 trang 81 Toán 7 Tập 2:
a) Có một chi tiết máy (đường viền ngoài là đường tròn) bị gãy (H.9.46). Làm thế nào để xác định được bán kính của đường tròn này?
b) Trên bản đồ, ba khu dân cư được quy hoạch tại ba điểm A, B, C không thẳng hàng. Hãy tìm trên bản đồ đó một điểm M cách đều A, B, C để quy hoạch một trường học.
Lời giải:
a)
Để xác định bán kính của đường tròn này ta thực hiện như sau:
Bước 1. Xác định 3 điểm A, B, C nằm trên đường viền của chi tiết máy.
Bước 2. Xác định các đường trung trực của tam giác ABC.
Bước 3. Xác định giao điểm O của ba đường trung trực của tam giác ABC.
Bước 4. Độ dài đoạn thẳng OB là bán kính của đường tròn.
b) Coi 3 điểm A, B, C là 3 đỉnh của tam giác ABC.
Do M cách đều A và B nên MA = MB.
Do đó M nằm trên đường trung trực của AB.
Do M cách đều B và C nên MB = MC.
Do đó M nằm trên đường trung trực của BC.
Vậy M là giao điểm 3 đường trung trực của tam giác ABC.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Bài 9.30 trang 81 Toán 7 Tập 2: Cho hai đường thẳng không vuông góc b, c cắt nhau tại điểm A và cho điểm H không thuộc b và c (H.9.47).
Hãy tìm điểm B thuộc b, điểm C thuộc c sao cho tam giác ABC nhận H làm trực tâm.
Lời giải:
Ta thực hiện theo các bước như sau:
Bước 1. Từ H kẻ đường thẳng vuông góc với đường thẳng b và cắt đường thẳng c tại một điểm. Điểm này chính là điểm C.
Bước 2. Từ H kẻ đường thẳng vuông góc với đường thẳng c và cắt đường thẳng b tại một điểm. Điểm này chính là điểm B.
Bước 3. Nối hai điểm B, C ta được tam giác ABC.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Với giải sách bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 35.
Với giải vở thực hành Toán lớp 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài 35.
Với tóm tắt lý thuyết Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.
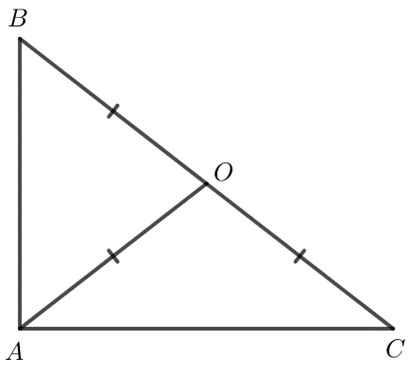
1. Sự đồng quy của ba đường trung trực trong một tam giác
a) Đường trung trực của tam giác
Trong tam giác ABC, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác. Ở hình dưới đây, a là đường trung trực ứng với cạnh BC của tam giác ABC.
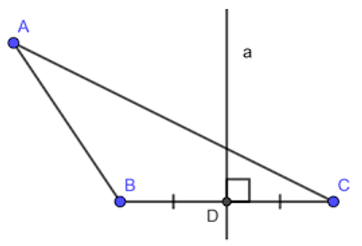
b) Sự đồng quy của ba đường trung trực
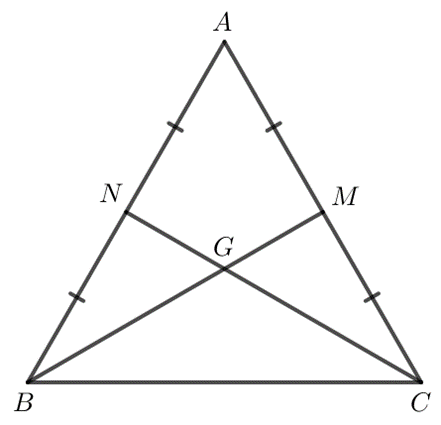
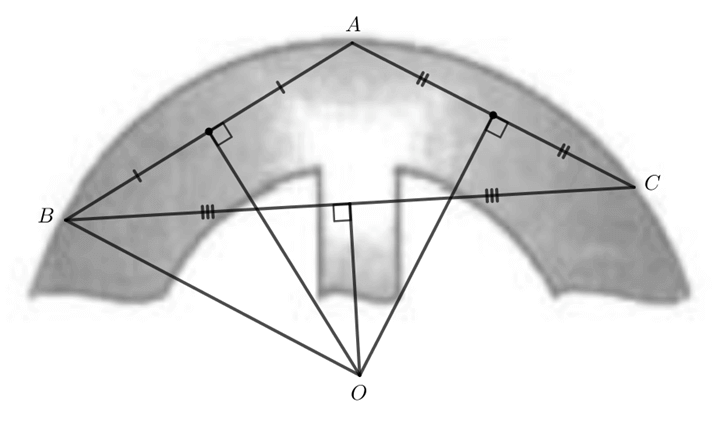
Định lí 1: Ba đường trung trực của một tam giác đồng quy tại một điểm. Điểm này cách đều ba đỉnh của tam giác.
Ví dụ: Trong tam giác ABC có các đường trung trực a, b, c đồng quy tại điểm O.
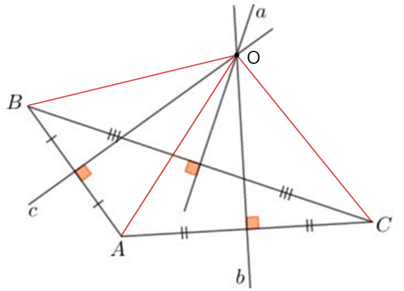
Khi đó: OA = OB = OC.
Nhận xét: Vì giao điểm O của ba đường trung trực trong tam giác ABC cách đều ba đỉnh của tam giác đó (OA = OB = OC) nên có một đường tròn tâm O đi qua ba đỉnh A, B, C.
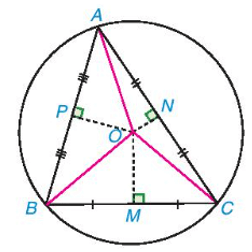
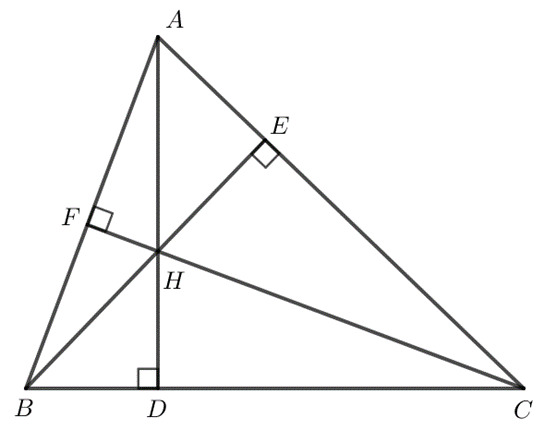
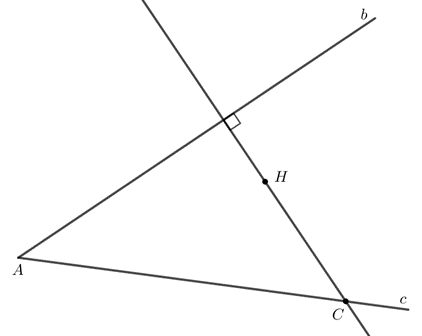
2. Sự đồng quy của ba đường cao trong tam giác
a) Đường cao của tam giác
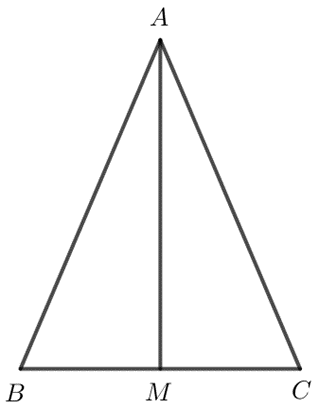
Trong hình dưới đây, đoạn thẳng AH kẻ từ đỉnh A, vuông góc với cạnh đối diện BC là một đường cao của tam giác ABC. Ta còn nói AH là đường cao xuất phát từ đỉnh A (hay đường cao ứng với cạnh BC).
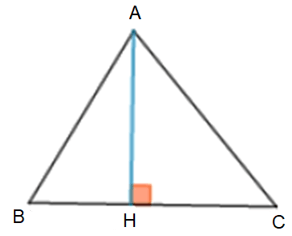
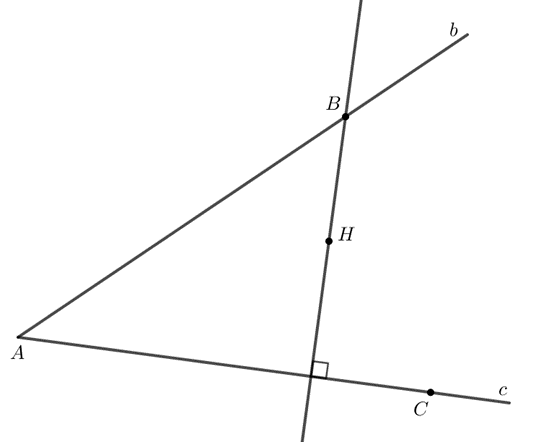
b) Sự đồng quy của ba đường cao
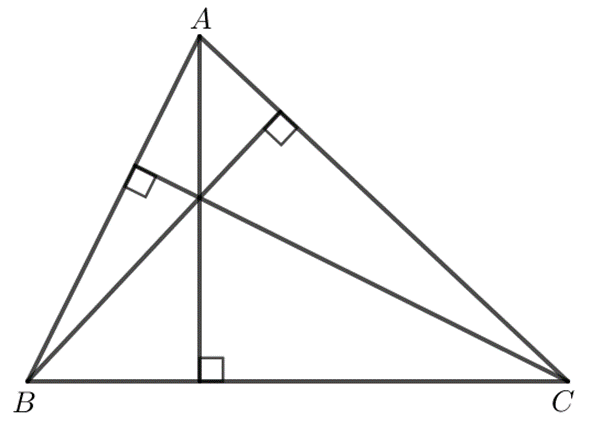
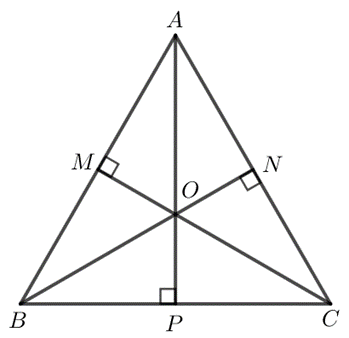
Định lí 2: Ba đường cao của một tam giác đồng quy tại một điểm.
Ví dụ: Trong tam giác ABC có các đường cao AI, BJ, CK đồng quy tại điểm H.
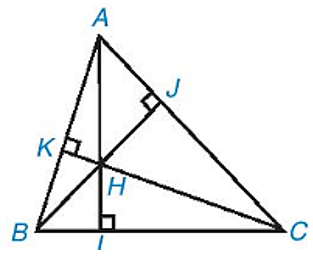
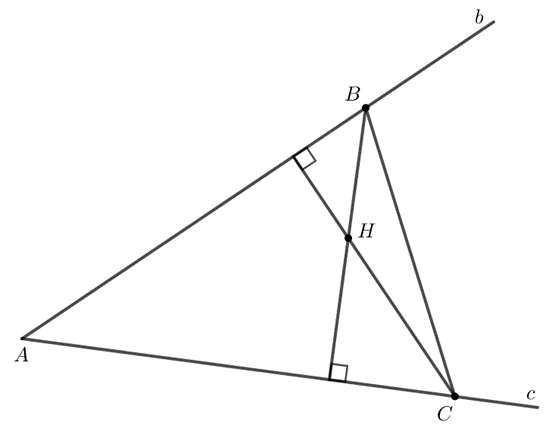
Chú ý:
- Điểm đồng quy của ba đường cao của một tam giác gọi là trực tâm của tam giác đó.
Ví dụ:Cho tam giác ABC có các đường cao AI, BJ, CK đồng quy tại điểm H.
Khi đó, H được gọi là trực tâm của tam giác ABC.
- Gọi H là trực tâm của tam giác ABC, ta có:
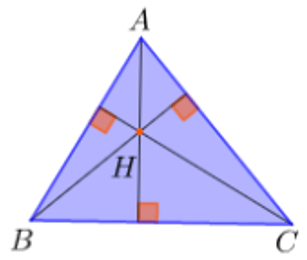
+) Khi ABC là tam giác nhọn thì H nằm bên trong tam giác.
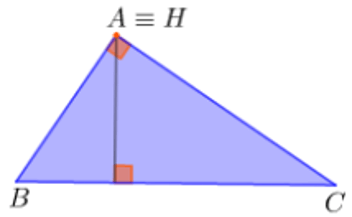
+) Khi ABC là tam giác vuông thì H trùng với A (kí hiệu H ≡ A).
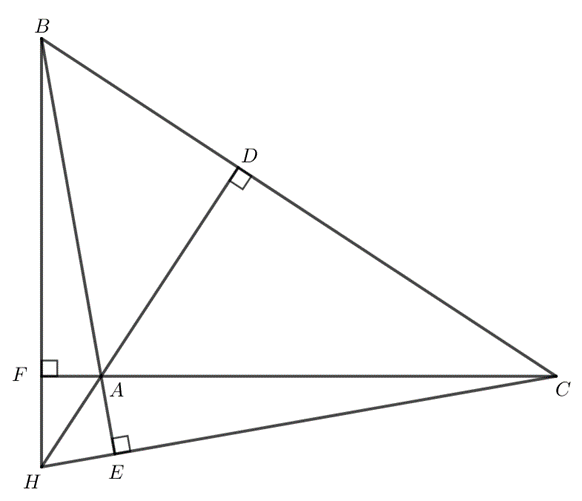
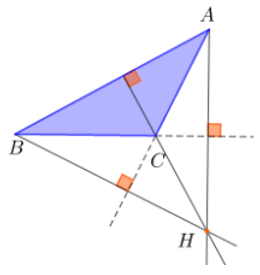
+) Khi ABC là tam giác tù thì H nằm bên ngoài tam giác.
Bài 1: Cho tam giác ABC vuông. Kẻ đường thẳng vuông góc với cạnh huyền BC của tam giác ABC tại điểm D không thuộc đoạn BC. Nó cắt đường thẳng chứa cạnh AB tại E và cắt đường thẳng chứa cạnh AC tại F. Xác định trực tâm của tam giác BEF.
Hướng dẫn giải
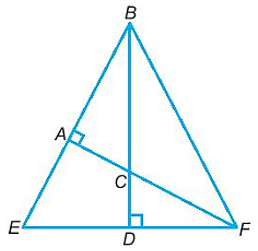
Trong tam giác BEF, đường cao xuất phát từ B là đường thẳng BD, đường cao xuất phát từ F là đường thẳng FA.
Hai đường cao BD và FA cắt nhau tại C.
Vậy suy ra C là trực tâm của tam giác BEF.
Bài 2: Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox là đường trung trực của đoạn thẳng PM, gọi N là điểm sao cho Oy là đường trung trực của đoạn thẳng PN. Đường thẳng MN cắt Ox tại R, cắt Oy tại S. Chứng minh tia PO là tia phân giác của góc RPS.
Hướng dẫn giải
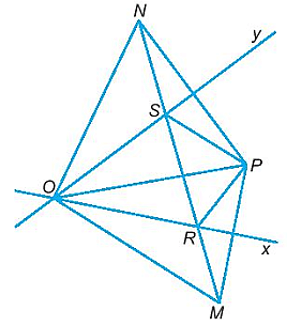
Tam giác OPM là tam giác cân tại O (Vì Ox là đường trung trực của đoạn thẳng PM)
Suy ra (1) và OM = OP.
Lại có tam giác RPM là tam giác cân tại R (Vì Ox, hay chính là Rx là đường trung trực của đoạn thẳng PM).
Suy ra (2)
Trừ vế với vế của (1) cho (2) ta có:
Hay (*)
Tương tự ta có tam giác OPN là tam giác cân tại O (Vì Oy là đường trung trực của đoạn thẳng PN)
Suy ra (3) và ON = OP.
Lại có tam giác SPN là tam giác cân tại R (Vì Oy, hay chính là Sy là đường trung trực của đoạn thẳng PN).
Suy ra (4)
Trừ vế với vế của (3) cho (4) ta có:
.
Hay (**)
Vì OM = ON (= OP) nên tam giác OMN là tam giác cân tại O.
Do đó: (***)
Từ (*), (**), (***) ta suy ra được .
Vậy suy ra PO là tia phân giác của góc RPS (đpcm).
Bài 3: Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh .
Hướng dẫn giải
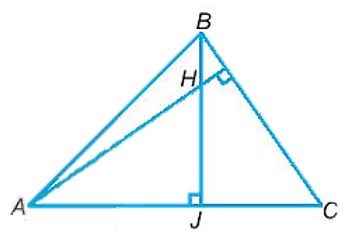
Gọi BJ là đường cao xuất phát từ B của tam giác ABC.
Xét hai tam giác AHJ và tam giác BCJ có:
AH = BC (gt)
(cùng phụ với )
Do đó ∆AHJ = ∆BCJ (cạnh huyền – góc nhọn)
Suy ra AJ = BJ (hai cạnh tương ứng)
Xét tam giác JAB vuông tại J và có AJ = BJ (cmt)
Nên JAB là tam giác vuông cân tại J.
Vậy (đpcm).
Các bài học để học tốt Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác Toán lớp 7 hay khác:
Với 15 bài tập trắc nghiệm Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.
Chỉ 150k mua trọn bộ trắc nghiệm Toán 7 Kết nối tri thức (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: