Toán 8 Cánh diều Bài 7: Trường hợp đồng dạng thứ hai của tam giác
Giải Toán 8 | No tags
Mục lục
- Đang tải mục lục...
Khởi động trang 79 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
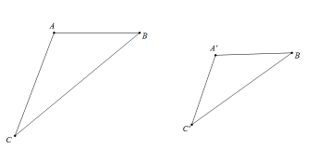
Khởi động trang 79 Toán 8 Tập 2: Bạn Hoàng và bạn Thu cùng vẽ bản đồ một ốc đảo và ba vị trí với tỉ lệ bản đồ khác nhau. Bạn Hoàng dùng ba điểm A, B, C lần lượt biểu thị các vị trí thứ nhất, thứ hai, thứ ba (Hình 68a). Bạn Thu dùng ba điểm A’, B’, C’ lần lượt biểu thị ba vị trí đó (Hình 68b).
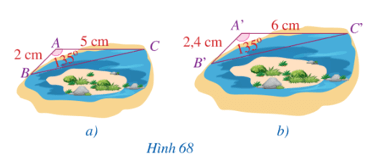
Hai tam giác A’B’C và ABC có đồng dạng hay không?
Lời giải:
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Ta có: Do đó
Xét ∆A’B’C’ và ∆ABC có:
Suy ra ∆A’B’C’ ᔕ ∆ABC (c.g.c).
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác:
Hoạt động 1 trang 79 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Hoạt động 1 trang 79 Toán 8 Tập 2:
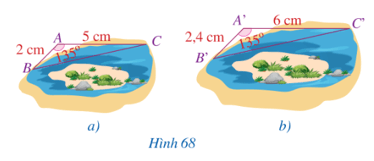
Quan sát Hình 68 và so sánh:
a) Các tỉ số và
b) Các góc và
Lời giải:
a) Ta có: Do đó
b) Ta có:
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác:
Luyện tập 1 trang 80 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Luyện tập 1 trang 80 Toán 8 Tập 2: Cho hai tam giác ABC và A’B’C’ thoả mãn AB = 2, AC = 3, A’B’ = 6, A’C’ = 9 và Chứng minh
Lời giải:
Ta có Suy ra
Xét ∆ABC và ∆A’B’C’, có:
Suy ra ∆ABC ᔕ ∆A’B’C’ (c.g.c)
Do đó (các cặp góc tương ứng).
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác:
Luyện tập 2 trang 80 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Luyện tập 2 trang 80 Toán 8 Tập 2: Cho góc xOy. Trên tia Ox lấy các điểm A, B sao cho OA = 2cm, OB = 9cm. Trên tia Oy lấy các điểm M, Nsao cho OM = 3cm, ON = 6cm. Chứng minh
Lời giải:
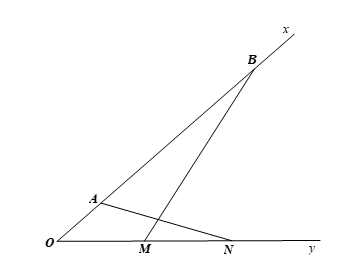
Xét hai tam giác OBM và ONA, ta có: Suy ra
Lại có là góc chung. Suy ra ∆OBM ᔕ ∆ONA (c.g.c).
Do đó (hai góc tương ứng).
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác:
Hoạt động 2 trang 81 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Hoạt động 2 trang 81 Toán 8 Tập 2: Cho hai tam giác ABC và A’B’C’ có:(Hình 72). Chứng minh ∆A’B’C’ ᔕ ∆ABC.
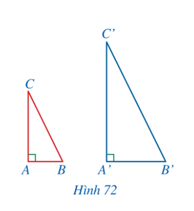
Lời giải:
Xét ∆A’B’C’ và ∆ABC có:
Suy ra ∆A’B’C’ ᔕ∆ABC (c.g.c).
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác:
Luyện tập 3 trang 81 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Luyện tập 3 trang 81 Toán 8 Tập 2: Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ sao cho Chứng minh
Lời giải:
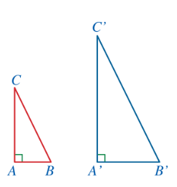
Ta có nên
Xét ∆ABC và ∆A’B’C’, ta có: và
Suy ra ∆ABC ᔕ ∆A’B’C’ (c.g.c).
Do đó (hai góc tương ứng).
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác:
Bài 1 trang 81 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Bài 1 trang 81 Toán 8 Tập 2: Cho Hình 74.
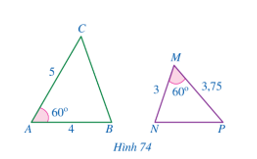
a) Chứng minh ∆ABC ᔕ ∆MNP.
b) Góc nào của tam giác ∆MNP bằng góc B?
c) Góc nào của tam giác ∆ABC bằng góc P?
Lời giải:
a) Ta có Suy ra
Xét ∆ABC và ∆MNP có:
và
Vậy ∆ABC ᔕ ∆MNP (c.g.c).
b) ∆ABC ᔕ ∆MNP, suy ra (hai góc tương ứng).
c) ∆ABC ᔕ ∆MNP, suy ra (hai góc tương ứng).
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác:
Bài 2 trang 82 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Bài 2 trang 82 Toán 8 Tập 2: Cho Hình 75, chứng minh:
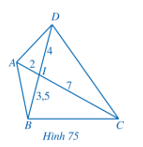
a) ∆IAB ᔕ ∆IDC;
b) ∆IAD ᔕ ∆IBC.
Lời giải:
a) Ta có Suy ra
Xét ∆IAB và ∆IDC có:
(đối đỉnh) và
Vậy ∆IAB ᔕ ∆IDC (c.g.c).
b) Ta có Suy ra
Xét ∆IAD và ∆IBC có:
(đối đỉnh) và
Vậy ∆IAD ᔕ ∆IBC (c.g.c).
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác:
Bài 3 trang 82 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
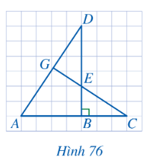
Bài 3 trang 82 Toán 8 Tập 2: Cho Hình 76, biết AB = 4, BC = 3, BE = 2, BD = 6. Chứng minh:
a) ∆ABD ᔕ ∆EBC;
b)
c) Tam giác DGE vuông.
Lời giải:
a) Ta có Suy ra
Xét∆ABD và ∆EBCcó:
và
Vậy ∆ABD ᔕ ∆EBC (c.g.c).
b) Do ∆ABD ᔕ ∆EBC (câu a), suy ra (hai góc tương ứng)
Mà (đối đỉnh) nên
c) Ta có (tổng hai góc nhọn của ∆ABD vuông tại B bằng 90°)
Mà (câu b)
Suy ra hay
Xét ∆GDE có (tổng ba góc của một tam giác)
Suy ra
Vậy tam giác DGE vuông tại G.
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác:
Bài 4 trang 82 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Bài 4 trang 82 Toán 8 Tập 2: Cho Hình 77, chứng minh:
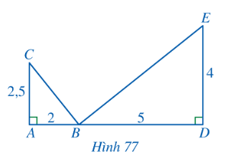
a)
b) BC ⊥ BE.
Lời giải:
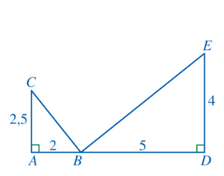
a) Ta có Suy ra
Xét ∆ABC và ∆DEB có:
Suy ra ∆ABC ᔕ ∆DEB (c.g.c).
Do đó (hai góc tương ứng).
b) Ta có (tổng hai góc nhọn của ∆BDE vuông tại D bằng 90°)
Mà (câu a)
Suy ra
Lại có
Nên
Do đó BC ⊥ BE.
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác:
Bài 5 trang 82 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Bài 5 trang 82 Toán 8 Tập 2: Cho ∆ABC ᔕ ∆MNP.
a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh ∆ABD ᔕ ∆MNQ.
b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh ∆ABG ᔕ ∆MNK.
Lời giải:
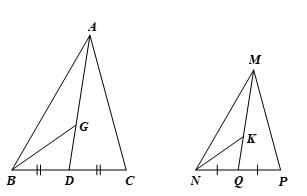
a) Vì ∆ABC ᔕ ∆MNP (giả thiết) nên và
Vì D, Q lần lượt là trung điểm của BC và NP nên
Do đó suy ra
Xét ∆ABDvà ∆MNQ có:
(do
Suy ra ∆ABD ᔕ ∆MNQ (c.g.c).
b) Vì ∆ABD ᔕ ∆MNQ (câu a) (hai góc tương ứng) và (tỉ số đồng dạng)
Mà G, K lần lượt là trọng tâm của hai tam giác ABC và MNP nên
Do đó
Xét ∆ABG và ∆MNK có:
(do
Vậy ∆ABG ᔕ ∆MNK (c.g.c).
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác:
Bài 6 trang 82 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Bài 6 trang 82 Toán 8 Tập 2: Cho Hình 78, biết AH2 = BH.CH. Chứng minh:
a) ∆HAB ᔕ ∆HCA;
b) Tam giác ∆ABC vuông tại A.
Lời giải:
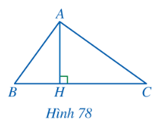
a) Từ AH2 = BH.CH ta có
Xét ∆HAB và ∆HCA có:
Suy ra ∆HAB ᔕ ∆HCA (c.g.c).
b) Vì ∆HAB ᔕ ∆HCA (câu a) nên (hai góc tương ứng).
Mà (tổng hai góc nhọn của ∆ABH vuông tại H bằng 90°)
Suy ra hay
Vậy ∆ABC vuông tại A.
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác:
Bài 7 trang 82 Toán 8 Tập 2 Cánh diều
Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác - Cánh diều
Bài 7 trang 82 Toán 8 Tập 2: Đố. Chỉ sử dụng thước thẳng có chia đơn vị đến milimét và thước đo góc, làm thế nào đo được khoảng cách giữa hai vị trí B, C trên thực tế, biết rằng có vị trí A thoả mãn AB = 20 m, AC = 50 m,
Bạn Vy làm như sau: Vẽ tam giác A’B’C’ có A’B’ = 2 cm, A’C’ = 5 cm, Bạn Vy lấy thước đo khoảng cách giữa hai điểm B’, C’ và nhận được kết quả B’C’ ≈ 6,6 cm. Từ đó, bạn Vy kết luận khoảng cách giữa hai vị trí B, C trên thực tế khoảng 66 m. Em hãy giải thích tại sao bạn Vy có thể kết luận như vậy.
Lời giải:
Đổi A’B’ = 2 cm = 0,02 m;
A’C’ = 5 cm = 0,05 m;
B’C’ = 6,6 cm = 0,066 m.
Ta có
Do đó
Xét ∆ABC và ∆A’B’C’ có:
Suy ra ∆ABC ᔕ ∆A’B’C’ (c.g.c)
Do đó
Nên BC = 1 000 . B’C’ = 1 000 . 0,066 = 66 (m).
Vậy khoảng cách giữa hai vị trí B, C trên thực tế khoảng 66m.
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay, chi tiết khác: