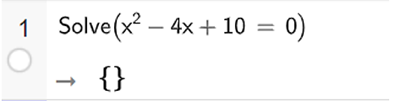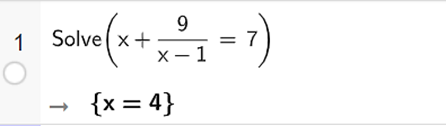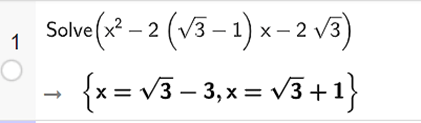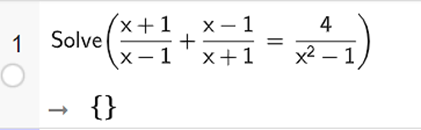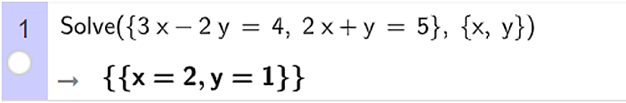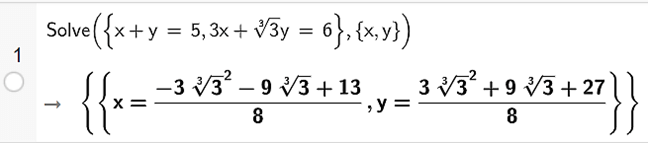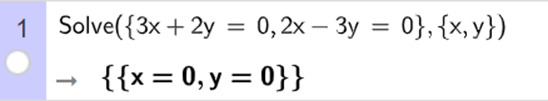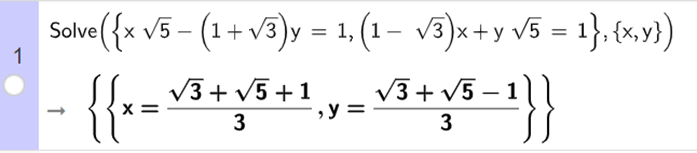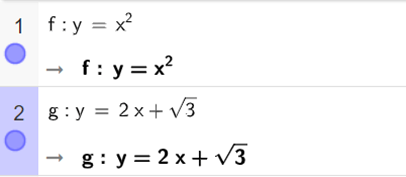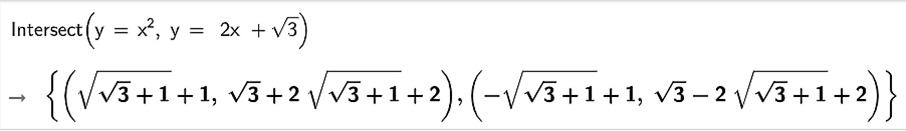Với giải bài tập Toán 9 Giải phương trình hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 9.

Giải Toán 9 Kết nối tri thức Giải phương trình hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra

Giải Toán 9 trang 114

Thực hành 1 trang 114 Toán 9 Tập 2 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra - Kết nối tri thức

Thực hành 1 trang 114 Toán 9 Tập 2: Giải các phương trình sau:

a) x² – 4x + 10 = 0;

b) $x+\frac{9}{x-1}=7;$

c) $x^2-2\left(\sqrt{3}-1\right)x-2\sqrt{3}=0$;

d) $\frac{x+1}{x-1}+\frac{x-1}{x+1}=\frac{4}{x^2-1}.$.

Lời giải:

Bước 1. Khởi động phần mềm Geogebrra , chọn Complex Adaptive System (CAS).

Bước 2. Ta dùng lệnh Solve () hoặc Solitions () trên ô lệnh của cửa sổ CAS để giải phương trình.

a) x² – 4x + 10 = 0

Ta nhập Solve (x^2 – 4x + 10 = 0), ta thu được kết quả như hình vẽ.

Vậy phương trình đã cho vô nghiệm.

b) $x+\frac{9}{x-1}=7$

Ta nhập Solve (x + 9/(x – 1) = 7), ta thu được kết quả như hình vẽ.

Vậy phương trình đã cho có nghiệm x = 4.

c) $x^2-2\left(\sqrt{3}-1\right)x-2\sqrt{3}=0$

Ta nhập Solve (x^2 – 2(sqrt(3) – 1) – 2sqrt(3) = 0), ta thu được kết quả như hình vẽ.

Vậy phương trình đã cho có hai nghiệm x = $\sqrt{3}$ - 3 và x = $\sqrt{3}$ + 1.

d) $\frac{x+1}{x-1}+\frac{x-1}{x+1}=\frac{4}{x^2-1}.$

Ta nhập Solve ((x + 1)/(x – 1) + (x – 1)/(x + 1)  = 4/(x^2 – 1)), ta thu được kết quả như hình vẽ.

Vậy phương trình đã cho vô nghiệm.

Lời giải bài tập Toán 9 Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra hay, chi tiết khác:

Thực hành 2 trang 114 Toán 9 Tập 2 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra - Kết nối tri thức

Thực hành 2 trang 114 Toán 9 Tập 2: Giải các hệ phương trình sau:

a) $\left\{\begin{array}{l}3x-2y=4\\ 2x+y=5;\end{array}\right.$

b) $\left\{\begin{array}{l}x+y=5\\ 3x+\sqrt[3]{3}y=6;\end{array}\right.$

c) $\left\{\begin{array}{l}3x+2y=0\\ 2x-3y=0;\end{array}\right.$

d) $\left\{\begin{array}{l}x\sqrt{5}-\left(1+\sqrt{3}\right)y=1\\ \left(1-\sqrt{3}\right)x+y\sqrt{5}=1.\end{array}\right.$

Lời giải:

Bước 1. Khởi động phần mềm Geogebrra , chọn Complex Adaptive System (CAS).

Bước 2.

: Ta dùng lệnh Solve ({, }), {, }), hoặc Solitions ({, }), {, }) trên ô lệnh của cửa sổ CAS để giải hệ phương trình.

: Sử dụng câu lệnh Intersect ({, (}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng.

a) $\left\{\begin{array}{l}3x-2y=4\\ 2x+y=5\end{array}\right.$

Ta nhập Solve ({3x – 2y = 4, 2x + y = 5}, {x, y}), ta thu được kết quả như hình vẽ.

Vậy hệ phương trình đã cho có nghiệm là x = 2; y = 1.

b) $\left\{\begin{array}{l}x+y=5\\ 3x+\sqrt[3]{3}y=6\end{array}\right.$

Ta nhập Solve ({x + y = 5, 3x + cbrt(3)y = 6}, {x, y}), ta thu được kết quả như hình vẽ.

Vậy hệ phương trình đã cho có nghiệm là $x=\frac{-3{\sqrt[3]{3}}^2-9\sqrt[3]{3}+13}{8};y=\frac{3{\sqrt[3]{3}}^2+9\sqrt[3]{3}+27}{8}.$

c) $\left\{\begin{array}{l}3x+2y=0\\ 2x-3y=0\end{array}\right.$

Ta nhập Solve ({3x + 2y = 0, 2x – 3y = 0}, {x, y}), ta thu được kết quả như hình vẽ.

Vậy hệ phương trình đã cho có nghiệm là x = 0; y = 0.

c) $\left\{\begin{array}{l}x\sqrt{5}-\left(1+\sqrt{3}\right)y=1\\ \left(1-\sqrt{3}\right)x+y\sqrt{5}=1\end{array}\right.$

Ta nhập Solve ({x sqrt(5) – (1 + sqrt(3))y = 1, (1 – sqrt(3))x – y sqrt(5) = 1}, {x, y}), ta thu được kết quả như hình vẽ.

Vậy hệ phương trình đã cho có nghiệm là $x=\frac{\sqrt{3}+\sqrt{5}+1}{3};y=\frac{\sqrt{3}+\sqrt{5}-1}{3}.$

Lời giải bài tập Toán 9 Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra hay, chi tiết khác:

Thực hành 3 trang 114 Toán 9 Tập 2 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra - Kết nối tri thức

Thực hành 3 trang 114 Toán 9 Tập 2: Cho đường thẳng (d): y = 2x + $\sqrt{3}$ và parabol (P): y = x².

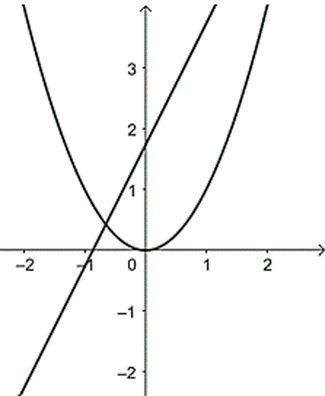
a) Vẽ đường thẳng (d) và parabol (P) trên cùng một mặt phẳng tọa độ.

b) Tìm tọa độ giao điểm của (d) và (P).

Lời giải:

Khởi động GeoGebra và đồng thời chọn hai chế độ Graphic 2 và CAS để vẽ đồ thị của đường thẳng (d): y = 2x + $\sqrt{3}$ và parabol (P): y = x².

a) Nhập công thức hàm số y = x² và y = 2x + $\sqrt{3}$ vào từng ô lệnh trong cửa sổ CAS.

Nháy chuột chọn nút ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.

Ta vẽ đường thẳng (d) và parabol (P) trên cùng một mặt phẳng tọa độ như sau:

b) Sử dụng câu lệnh Intersect ({, (}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng.

Ta nhập Intersect ({y = x², y = 2x + $\sqrt{3}$), ta thu được kết quả như hình vẽ.

Vậy hai hàm số đã cho giao nhau tại hai điểm là $\left(\sqrt{\sqrt{3}+1}+1;\sqrt{3}+2\sqrt{\sqrt{3}+1}+2\right),$ $\left(-\sqrt{\sqrt{3}+1}+1;\sqrt{3}-2\sqrt{\sqrt{3}+1}+2\right).$

Lời giải bài tập Toán 9 Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra hay, chi tiết khác: