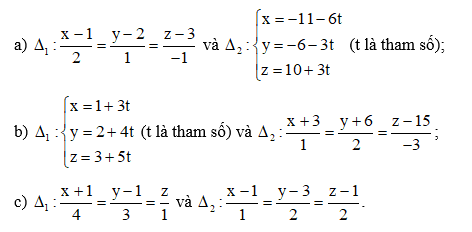Bài 6 trang 79 Toán 12 Tập 2 Cánh diều

Giải Toán 12 Bài 2: Phương trình đường thẳng - Cánh diều

Bài 6 trang 79 Toán 12 Tập 2: Xác định vị trí tương đối của hai đường thẳng ∆₁, ∆₂ trong mỗi trường hợp sau:

Lời giải:

a) Đường thẳng ∆₁ đi qua điểm M₁(1; 2; 3) và có $\overrightarrow{u_1}=\left(2;1;-1\right)$ là vectơ chỉ phương.

Đường thẳng ∆₂ đi qua điểm M₂(– 11; – 6; 10) và có $\overrightarrow{u_2}=\left(-6;-3;3\right)$ là vectơ chỉ phương.

Ta có$-3\overrightarrow{u_1}=\overrightarrow{u_2}$, suy ra $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ cùng phương;

$\overrightarrow{M_1{M}_2}=\left(-12;-8;7\right)$ và $\frac{-12}{2}\ne \frac{-8}{1}$ nên $\overrightarrow{u_1},\overrightarrow{M_1{M}_2}$ không cùng phương.

Vậy ∆₁ // ∆₂.

b) Đường thẳng ∆₁ đi qua điểm M₁(1; 2; 3) và có $\overrightarrow{u_1}=\left(3;4;5\right)$ là vectơ chỉ phương.

Đường thẳng ∆₂ đi qua điểm M₂(– 3; – 6; 15) và có $\overrightarrow{u_2}=\left(1;2;-3\right)$ là vectơ chỉ phương.

Ta có:$\frac{3}{1}\ne \frac{4}{2}$, suy ra $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ không cùng phương;

$\overrightarrow{M_1{M}_2}=\left(-4;-8;12\right)$, $\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]=\left(\left|\begin{array}{cc}4& 5\\ 2& -3\end{array}\right|;\left|\begin{array}{cc}5& 3\\ -3& 1\end{array}\right|;\left|\begin{array}{cc}3& 4\\ 1& 2\end{array}\right|\right)=\left(-22;14;2\right)$.

Do $\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]\cdot \overrightarrow{M_1{M}_2}=$ (– 22) ∙ (– 4) + 14 ∙ (– 8) + 2 ∙ 12 = 0 nên $\overrightarrow{u_1},\overrightarrow{u_2},\overrightarrow{M_1{M}_2}$ đồng phẳng.

Vậy ∆₁ cắt ∆₂.

c) Đường thẳng ∆₁ đi qua điểm M₁(– 1; 1; 0) và có $\overrightarrow{u_1}=\left(4;3;1\right)$ là vectơ chỉ phương.

Đường thẳng ∆₂ đi qua điểm M₂(1; 3; 1) và có $\overrightarrow{u_2}=\left(1;2;2\right)$ là vectơ chỉ phương.

Ta có: $\overrightarrow{M_1{M}_2}=\left(2;2;1\right)$,$\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]=\left(\left|\begin{array}{cc}3& 1\\ 2& 2\end{array}\right|;\left|\begin{array}{cc}1& 4\\ 2& 1\end{array}\right|;\left|\begin{array}{cc}4& 3\\ 1& 2\end{array}\right|\right)=\left(4;-7;5\right)$.

Do $\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]\cdot \overrightarrow{M_1{M}_2}=$ 4 ∙ 2 + (– 7) ∙ 2 + 5 ∙ 1 = – 1 ≠ 0 nên $\overrightarrow{u_1},\overrightarrow{u_2},\overrightarrow{M_1{M}_2}$không đồng phẳng.

Vậy ∆₁ và ∆₂ chéo nhau.

Lời giải bài tập Toán 12 Bài 2: Phương trình đường thẳng hay, chi tiết khác: