Hoạt động 5 trang 69 Toán 12 Tập 2 Cánh diều

Giải Toán 12 Bài 2: Phương trình đường thẳng - Cánh diều

Hoạt động 5 trang 69 Toán 12 Tập 2: Cho hai đường thẳng phân biệt ∆₁, ∆₂ lần lượt đi qua các điểm M₁, M₂ và tương ứng có vectơ chỉ phương là $\overrightarrow{u_1},\overrightarrow{u_2}$

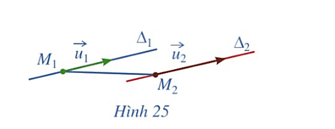
a) Giả sử ∆₁ song song với ∆₂ (Hình 25). Các cặp vectơ sau có cùng phương hay không: $\overrightarrow{u_1}$và $\overrightarrow{u_2}$; $\overrightarrow{u_1}$ và $\overrightarrow{M_1{M}_2}$?

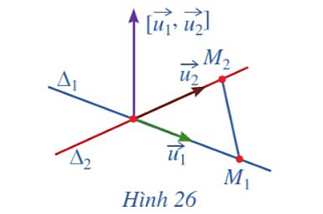
b) Giả sử ∆₁ và ∆₂ cắt nhau (Hình 26). Hai vectơ $\overrightarrow{u_1}$ và $\overrightarrow{u_2}$ có cùng phương hay không? Ba vectơ $\overrightarrow{u_1}$,$\overrightarrow{u_2}$ và $\overrightarrow{M_1{M}_2}$ có đồng phẳng hay không?

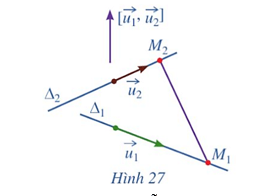
c) Giả sử ∆₁ và ∆₂ chéo nhau (Hình 27). Hai vectơ $\overrightarrow{u_1}$ và $\overrightarrow{u_2}$ có cùng phương hay không? Ba vectơ $\overrightarrow{u_1}$,$\overrightarrow{u_2}$ và $\overrightarrow{M_1{M}_2}$ có đồng phẳng hay không?

Lời giải:

a) Vì ∆₁ song song với ∆₂ nên hai vectơ $\overrightarrow{u_1}$ và $\overrightarrow{u_2}$ cùng phương; hai vectơ $\overrightarrow{u_1}$ và $\overrightarrow{M_1{M}_2}$ không cùng phương.

b) Vì ∆₁ và ∆₂ cắt nhau nên hai vectơ $\overrightarrow{u_1}$ và $\overrightarrow{u_2}$ không cùng phương.

Ba vectơ $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ và $\overrightarrow{M_1{M}_2}$ đồng phẳng vì giá của mỗi vectơ này đều cùng nằm trong mặt phẳng chứa hai đường thẳng cắt nhau ∆₁ và ∆₂.

c) Vì ∆₁ và ∆₂ chéo nhau nên hai vectơ $\overrightarrow{u_1}$ và $\overrightarrow{u_2}$ không cùng phương.

Ba vectơ $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ và $\overrightarrow{M_1{M}_2}$ không đồng phẳng.

Lời giải bài tập Toán 12 Bài 2: Phương trình đường thẳng hay, chi tiết khác: