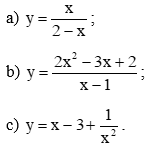Với giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 12 dễ dàng làm bài tập Toán 12 Bài 3.

Giải Toán 12 Cánh diều Bài 3: Đường tiệm cận của đồ thị hàm số

Giải Toán 12 trang 21

Câu hỏi khởi động trang 21 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

Câu hỏi khởi động trang 21 Toán 12 Tập 1: Số dân của một thị trấn sau x năm kể từ năm 1970 được ước tính bởi công thức

$y = f\left(x\right) = \frac{26x + 10}{x + 5}$

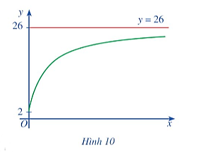
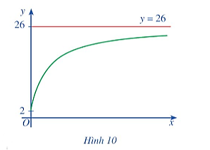
(f(x) được tính bằng nghìn người) (Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2020). Xem y = f(x) là một hàm số xác định trên nửa khoảng [0; + ∞), đồ thị của hàm số đó là đường cong màu xanh ở Hình 10.

Khi x → + ∞, đồ thị hàm số y = f(x) ngày càng “tiến gần” tới đường thẳng nào?

Lời giải:

Khi x → + ∞, đồ thị hàm số y = f(x) ngày càng “tiến gần” tới đường thẳng y = 26.

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

Hoạt động 1 trang 21 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

Hoạt động 1 trang 21 Toán 12 Tập 1: Xét hàm số y = f(x) = $\frac{26x + 10}{x + 5}$ , với x ∈ [0; + ∞) có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm $\underset{x\to +\infty }{\lim }$f(x) .

Lời giải:

Quan sát đồ thị ở Hình 10, ta thấy x → + ∞ thì y → 26.

Vậy $\underset{x\to +\infty }{\lim }$f(x) = 26.

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

Luyện tập 1 trang 22 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

Luyện tập 1 trang 22 Toán 12 Tập 1: Tìm tiệm cận ngang của đồ thị hàm số $y = \frac{3x - 2}{x + 1}$

Lời giải:

Hàm số đã cho có tập xác định là ℝ \ {– 1}.

Ta có: $\underset{x\to +\infty }{\lim }$y =$\underset{x\to +\infty }{\lim }$$\frac{3x - 2}{x + 1}$= 3 ,

          $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{3x-2}{x+1}=3$.

Vậy đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số đã cho.

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

Hoạt động 2 trang 22 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

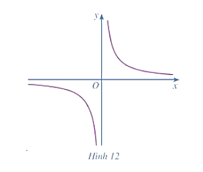
Hoạt động 2 trang 22 Toán 12 Tập 1: Cho hàm số y = f(x) = $\frac{1}{x}$ có đồ thị là đường cong như Hình 12

Tìm $\underset{x\to 0^{+}}{\lim }$f(x), $\underset{x\to 0^{-}}{\lim }$f(x)

Lời giải:

Quan sát đồ thị ở Hình 12, ta thấy:

+) x → 0⁺ thì f(x) → + ∞, do đó $\underset{x\to 0^{+}}{\lim }$f(x) = $+\infty$;

+) x → 0^– thì f(x) → – ∞, do đó $\underset{x\to 0^{-}}{\lim }$f(x) = -$\infty$.

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

Luyện tập 2 trang 23 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

Luyện tập 2 trang 23 Toán 12 Tập 1: Tìm tiệm cận đứng của đồ thị hàm số $y = \frac{x^2 + 3x}{x - 5}$

Lời giải:

Hàm số đã cho có tập xác định là ℝ\{5}.

Ta có $\underset{x\to 5^{+}}{\lim }$y =$\underset{x\to 5^{+}}{\lim }$$\frac{x^2+ 3x}{x - 5}$= +$\infty$  (do $\underset{x\to 5^{+}}{\lim }$$(x^2+3x) =40> 0$,$\underset{x\to 5^{+}}{\lim }$(x - 5) = 0  , khi x → 5⁺ thì x – 5 > 0).

Tương tự $\underset{x\to 5^{-}}{\lim }$y = $\underset{x\to 5^{-}}{\lim }$$\frac{x^2 + 3x}{x - 5}$ = - $\infty$.

Vậy đường thẳng x = 5 là tiệm cận đứng của đồ thị hàm số đã cho.

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

Hoạt động 3 trang 24 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

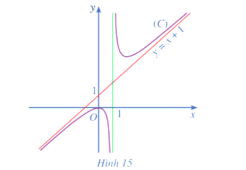
Hoạt động 3 trang 24 Toán 12 Tập 1: Cho hàm số y = f(x) = $x + 1 + \frac{1}{x - 1}$ có đồ thị là (C) và đường thẳng y = x + 1 (Hình 15)

Tìm $\underset{x\to +\infty }{\lim }$[f(x) - (x + 1)]; $\underset{x\to -\infty }{\lim }$[f(x) - (x + 1)] .

Lời giải:

Ta có $\underset{x\to +\infty }{\lim }$[f(x) - (x + 1)] = $\underset{x\to +\infty }{\lim }$$\frac{1}{x - 1}$ = 0;

$\underset{x\to -\infty }{\lim }$[f(x) - (x + 1)]= $\underset{x\to -\infty }{\lim }$$\frac{1}{x - 1}$= 0

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

Luyện tập 3 trang 25 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

Luyện tập 3 trang 25 Toán 12 Tập 1: Chứng minh rằng đường thẳng y = – x là tiệm cận xiên của đồ thị hàm số y = f(x) = $\frac{-x^2 - 2x +3}{x + 2}$.

Lời giải:

Do $\underset{x\to +\infty }{\lim }\left[f\left(x\right)-\left(-x\right)\right]=\underset{x\to +\infty }{\lim }\left[f\left(x\right)+x\right]$ = $\underset{x\to +\infty }{\lim }\left(\frac{-x^2-2x+3}{x+2}+x\right)$ = $\underset{x\to +\infty }{\lim }\frac{3}{x+2}$ = 0 nên đường thẳng y = – x là tiệm cận xiên của đồ thị hàm số đã cho.

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

Luyện tập 4 trang 26 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

Luyện tập 4 trang 26 Toán 12 Tập 1: Tìm tiệm cận xiên của đồ thị hàm số $y = f\left(x\right) = \frac{x^2 -3x + 2}{x + 3}$

Lời giải:

Ta có:  a = $\underset{x\to +\infty }{\lim }$$\frac{f\left(x\right)}{x}$= $\underset{x\to +\infty }{\lim }$$\frac{x^2- 3x + 2}{x(x + 3)}$= 1

và b = $\underset{x\to +\infty }{\lim }\left[f\left(x\right)-x\right]$ = $\underset{x\to +\infty }{\lim }\left(\frac{x^2-3x+2}{x+3}-x\right)$ = $\underset{x\to +\infty }{\lim }\frac{-6x+2}{x+3}$ = -6.

Vậy đường thẳng y = x – 6 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → + ∞).

Tương tự, do $\underset{x\to +\infty }{\lim }$$\frac{f\left(x\right)}{x}=1$  và $\underset{x\to +\infty }{\lim }$[f(x) -x] = - 6  nên đường thẳng y = x – 6 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → – ∞).

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

Bài 1 trang 27 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

Bài 1 trang 27 Toán 12 Tập 1: Tiệm cận đứng của đồ thị hàm số $y = \frac{x+ 2}{x + 1}$ là:

A. x = – 1.

B. x = – 2.

C. x = 1.

D. x = 2. 

Lời giải:

Đáp án đúng là: A

Hàm số đã cho có tập xác định là ℝ\{– 1}.

Ta có $\underset{x\to 1^{+}}{\lim }$y = $\underset{x\to 1^{+}}{\lim }$$\frac{x + 2}{x + 1}$= +$\infty$; $\underset{x\to 1^{-}}{\lim }$y = $\underset{x\to 1^{-}}{\lim }$$\frac{x + 2}{x + 1}$= - $\infty$.

Vậy đường thẳng x = – 1 là tiệm cận đứng của đồ thị hàm số đã cho.

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

Bài 2 trang 27 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

Bài 2 trang 27 Toán 12 Tập 1: Tiệm cận xiên của đồ thị hàm số $y = \frac{x^2+3x +5}{x + 2}$ là:

A. y = x.

B. y = x + 1.

C. y = x + 2.

D. y = x + 3.

Lời giải:

Đáp án đúng là: B

Ta có: a = $\underset{x\to +\infty }{\lim }$$\frac{y}{x}$= $\underset{x\to +\infty }{\lim }$$\frac{x^2+ 3x + 5}{x (x + 2)}$ = 1

và b = $\underset{x\to +\infty }{\lim }$[y - x] = $\underset{x\to +\infty }{\lim }$$\left(\frac{x^2+ 3x + 5}{x + 2} - x\right)$= $\underset{x\to +\infty }{\lim }$$\frac{x + 5}{x + 2}$= 1 .

Vậy đường thẳng y = x + 1 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → + ∞).

Tương tự, do $\underset{x\to -\infty }{\lim }$$\frac{y}{x}$= 1  và $\underset{x\to -\infty }{\lim }$[y - x] = 1 nên đường thẳng y = x + 1 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → – ∞).

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

Bài 3 trang 27 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

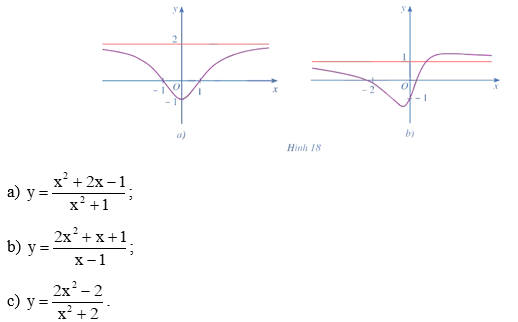
Bài 3 trang 27 Toán 12 Tập 1: Đồ thị hàm số ở Hình 18a, Hình 18b đều có đường tiệm cận ngang là đường thẳng màu đỏ. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau?

Lời giải:

Ta có $\underset{x\to +\infty }{\lim }$$\frac{x^2 + 2x -1}{x^2 + 1}$= 1; $\underset{x\to +\infty }{\lim }$$\frac{2x^2+ x + 1}{x - 1}= +\infty$; $\underset{x\to +\infty }{\lim }$$\frac{2x^2- 2}{x^2 + 2}= 2$.

• Xét đồ thị ở Hình 18a, ta thấy đường thẳng y = 2 là tiệm cận ngang của đồ thị này.

Lại có $\underset{x\to +\infty }{\lim }$$\frac{2x^2 - 2}{x^2 + 2}$= 2, vậy đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số y =$\frac{2x^2- 2}{x^2 + 2}$ . Khi đó, đồ thị hàm số ở Hình 18a là đồ thị của hàm số $y=\frac{2x^2-2}{x^2+2}$.

• Xét đồ thị ở Hình 18b, ta thấy đường thẳng y = 1 là tiệm cận ngang của đồ thị này.

Lại có $\underset{x\to +\infty }{\lim }$$\frac{x^2 + 2x -1}{x^2 + 1}$ = 1, vậy đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số y = $\frac{x^2 + 2x -1}{x^2 + 1}$ . Khi đó, đồ thị hàm số ở Hình 18b là đồ thị của hàm số y = $\frac{x^2 + 2x -1}{x^2 + 1}$ .

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

Bài 4 trang 27 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

Bài 4 trang 27 Toán 12 Tập 1: Tìm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có) của đồ thị mỗi hàm số sau:

Lời giải:

a) Hàm số đã cho có tập xác định là ℝ\{2}.

• Ta có $\underset{x\to 2^{-}}{\lim }$$\frac{x}{2 - x}= +\infty$, $\underset{x\to 2^{+}}{\lim }$$\frac{x}{2 - x}= -\infty$ .

Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số đã cho.

• Lại có $\underset{x\to +\infty }{\lim }$ $\frac{x}{2 - x}= -1$, $\underset{x\to -\infty }{\lim }$$\frac{x}{2 - x}= -1$.

Do đó, đường thẳng y = – 1 là tiệm cận ngang của đồ thị hàm số đã cho.

• Ta có $\underset{x\to +\infty }{\lim }$$\frac{y}{x}$= $\underset{x\to +\infty }{\lim }$$\frac{x}{(2 - x) x}$= $\underset{x\to +\infty }{\lim }$$\frac{1}{2 - x}$= $-\infty$ = 0.

Do đó, đồ thị hàm số y = $\frac{x}{2 - x}$  không có tiệm cận xiên.

b) Hàm số đã cho có tập xác định là ℝ\{1}.

• Ta có $\underset{x\to 1^{+}}{\lim }\frac{2x^2-3x+2}{x-1}=+\infty$; $\underset{x\to 1^{-}}{\lim }\frac{2x^2-3x+2}{x-1}=-\infty$.

Do đó, đường thẳng x = 1 tiệm cận đứng của đồ thị hàm số đã cho.

• Lại có $\underset{x\to +\infty }{\lim }$$\frac{2x^2 - 3x + 2}{x - 1}= +\infty$; $\underset{x\to -\infty }{\lim }$$\frac{2x^2 - 3x + 2}{x - 1}= -\infty$ .

Do đó, đồ thị hàm số đã cho không có tiệm cận ngang.

• Tiệm cận xiên của đồ thị hàm số đã cho có dạng y = ax + b.

Ta có:  a = $\underset{x\to +\infty }{\lim }$$\frac{y}{x}$= $\underset{x\to +\infty }{\lim }$$\frac{2x^2 - 3x + 2}{x (x - 1)}$= 2

và b = $\underset{x\to +\infty }{\lim }$[y - 2x]= $\underset{x\to +\infty }{\lim }$$\left(\frac{2x^2 - 3x + 2}{x - 1} - 2x\right)$= $\underset{x\to +\infty }{\lim }$$\frac{-x + 2}{x - 1}$= -1 .

Vậy đường thẳng y = 2x – 1 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → + ∞).

Tương tự, do $\underset{x\to -\infty }{\lim }$$\frac{y}{x}= 2$  và $\underset{x\to -\infty }{\lim }$[y - 2x] = -1  nên đường thẳng y = 2x – 1 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → – ∞).

c) Hàm số đã cho có tập xác định là ℝ\{0}.

• Ta có $\underset{x\to 0^{+}}{\lim }\left(x-3+\frac{1}{x^2}\right)=+\infty$; $\underset{x\to 0^{-}}{\lim }\left(x-3+\frac{1}{x^2}\right)=+\infty$.

Do đó, đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số đã cho.

• Lại có $\underset{x\to +\infty }{\lim }$$\left(x - 3 + \frac{1}{x^2}\right)$= + $\infty$; $\underset{x\to -\infty }{\lim }$$\left(x - 3 + \frac{1}{x^2}\right)$= - $\infty$.

Do đó, đồ thị hàm số đã cho không có tiệm cận ngang.

• Do $\underset{x\to +\infty }{\lim }$[y - (x - 3)] = $\underset{x\to +\infty }{\lim }$$\frac{1}{x^2}$= 0; $\underset{x\to -\infty }{\lim }$[y - (x - 3)] = $\underset{x\to -\infty }{\lim }$$\frac{1}{x^2}$= 0  nên đường thẳng y = x – 3 là tiệm cận xiên của đồ thị hàm số đã cho.

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

Bài 5 trang 27 Toán 12 Tập 1 Cánh diều

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

Bài 5 trang 27 Toán 12 Tập 1: Số lượng sản phẩm bán được của một công ty trong x (tháng) được tính theo công thức $S\left(x\right) = 200\left(5 - \frac{9}{2 + x} \right)$ , trong đó x ≥ 1 (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).

a) Xem y = S(x) là một hàm số xác định trên nửa khoảng [1; + ∞), hãy tìm tiệm cận ngang của đồ thị hàm số đó.

b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong x (tháng) khi x đủ lớn. 

Lời giải:

a) Xét hàm số y = S(x) = 200$\left(5 - \frac{9}{2 + x}\right)$  với x ∈ [1; + ∞).

Ta có $\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }200\left(5-\frac{9}{2+x}\right)=1000$.

Do đó, đường thẳng y = 1 000 là tiệm cận ngang của đồ thị hàm số đã cho trên nửa khoảng [1; + ∞).

b) Ta có đồ thị hàm số y = S(x) với x ∈ [1; + ∞) nhận đường thẳng y = 1 000 làm tiệm cận ngang, tức là khi x càng lớn thì số lượng sản phẩm bán được của công ty đó trong x (tháng) sẽ tiến gần đến 1 000 sản phẩm.

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác: