Luyện tập 5 trang 12 Toán 12 Tập 1 - Kết nối tri thức

Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức

Luyện tập 5 trang 12 Toán 12 Tập 1: Tìm cực trị của các hàm số sau:

a) y = x⁴ – 3x² + 1;

b) $y=\frac{-x^2+2x-1}{x+2}$.

Lời giải:

a) Tập xác định của hàm số là ℝ.

Ta có y' = 4x³ – 6x; y' = 0 ⇔ x = 0 hoặc x = $-\frac{\sqrt{6}}{2}$ hoặc $x=\frac{\sqrt{6}}{2}$.

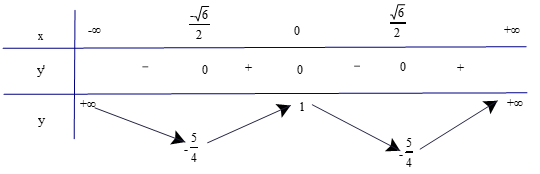
Lập bảng biến thiên của hàm số

Từ bảng biến thiên ta có:

Hàm số đạt cực tiểu tại $x=-\frac{\sqrt{6}}{2}$ và y_CT = $-\frac{5}{4}$.

Hàm số đạt cực đại tại x = 0 và y_CĐ = 1.

Hàm số đạt cực tiểu tại $x=\frac{\sqrt{6}}{2}$ và y_CT = $-\frac{5}{4}$.

b) Tập xác định của hàm số là ℝ\{−2}.

Có $y^{\text{'}}=\frac{\left(-2x+2\right)\left(x+2\right)-\left(-x^2+2x-1\right)}{{\left(x+2\right)}^2}=\frac{-x^2-4x+5}{{\left(x+2\right)}^2}$.

Có y' = 0⇔ −x² – 4x + 5 = 0 ⇔ x = 1 hoặc x = −5.

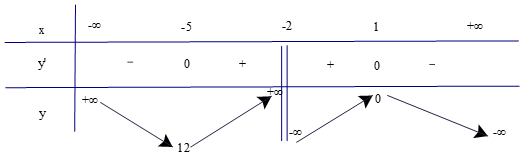
Lập bảng biến thiên của hàm số

Từ bảng biến thiên ta có:

Hàm số đạt cực tiểu tại x = −5 và y_CT = 12.

Hàm số đạt cực đại tại x = 1 và y_CĐ = 0.

Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác: