Hai đường thẳng song song và dấu hiệu nhận biết (Lý thuyết Toán lớp 7) - Kết nối tri thức
Với tóm tắt lý thuyết Toán 7 Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết sách Kết nối tri thức hay nhất, chi tiết
sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.
Hai đường thẳng song song và dấu hiệu nhận biết (Lý thuyết Toán lớp 7) - Kết nối tri thức
Lý thuyết Hai đường thẳng song song và dấu hiệu nhận biết
1. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
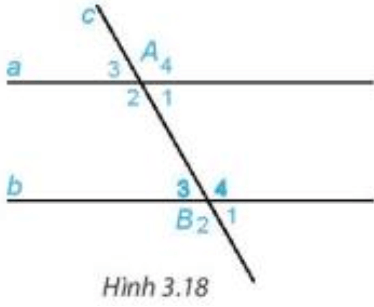
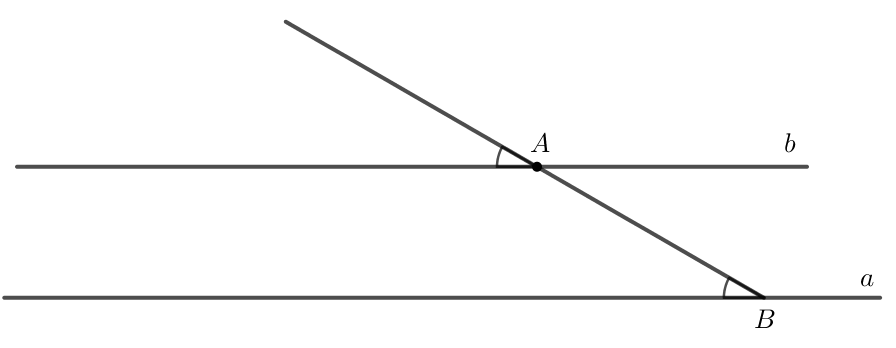
• Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại A và B tạo thành bốn góc đỉnh A và bốn góc đỉnh B. Khi đó ta có:
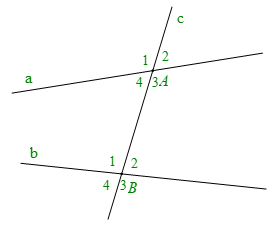
+ Các cặp góc so le trong là: A3 và B1; A4 và B2.
+ Các cặp góc đồng vị là: A1 và B1; A2 và B2; A3 và B3; A4 và B4.
+ Các cặp góc trong cùng phía là: A4 và B1; A3 và B2.
• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+ Hai góc so le trong còn lại bằng nhau.
+ Hai góc đồng vị bằng nhau.
Ví dụ:
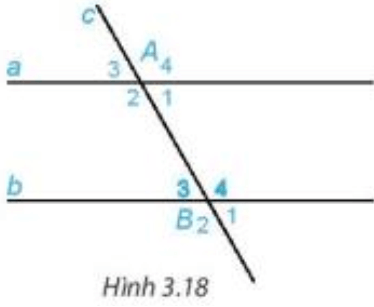
+ Cho đường thẳng c cắt hai đường thẳng phân biệt a, b lần lượt tại A và B.
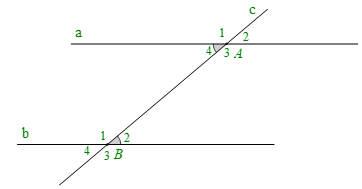
Ta có là cặp góc so le trong
Nếu thì cặp góc so le trong còn lại và các cặp góc đồng vị bằng nhau:
2. Dấu hiệu nhận biết hai đường thẳng song song
• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau. Kí hiệu là: .
• Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Ví dụ:
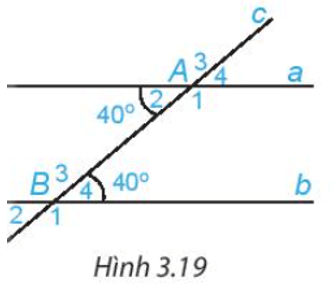
+ Cho hình vẽ:
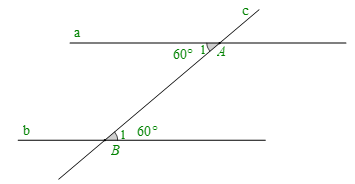
Ta có: . Mà hai góc ở vị trí so le trong.
Do đó: (dấu hiệu nhận biết hai đường thẳng song song).
+ Cho hình vẽ:
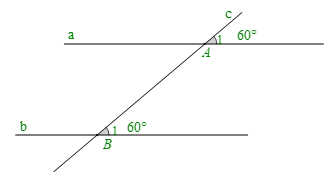
Ta có: . Mà hai góc ở vị trí đồng vị.
Do đó: (dấu hiệu nhận biết hai đường thẳng song song).
+ Cho hình vẽ:
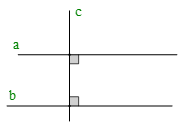
Ta có: và
Do đó: .
Chú ý:
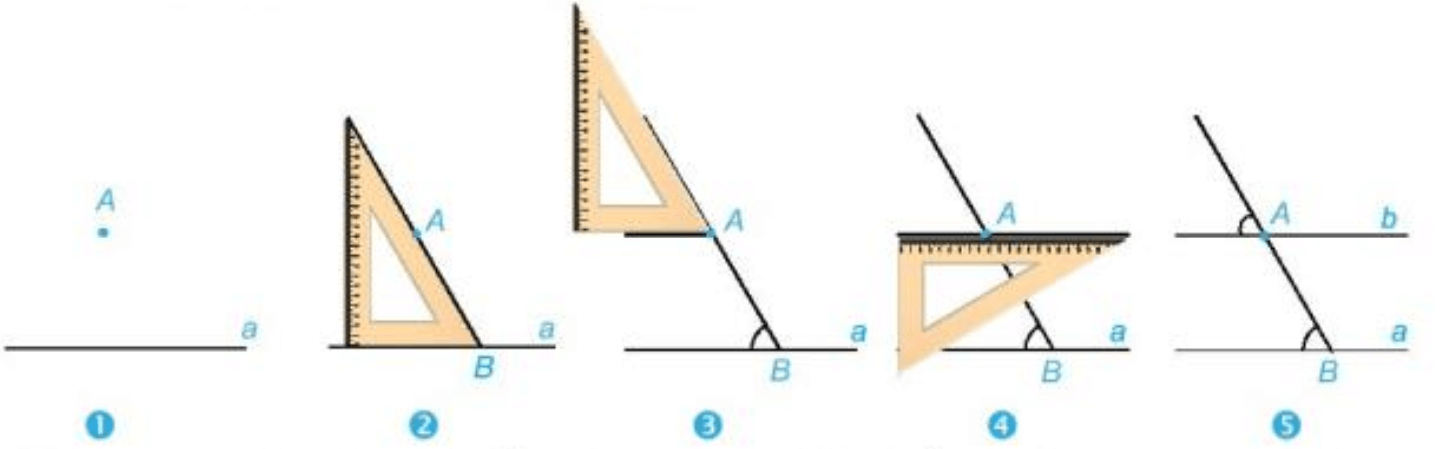
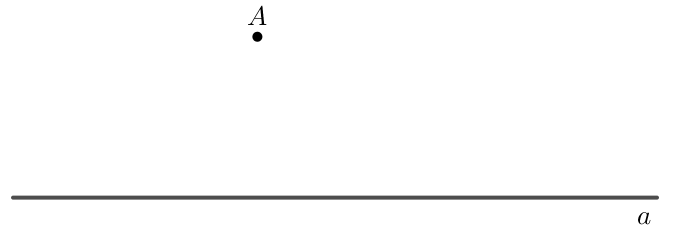
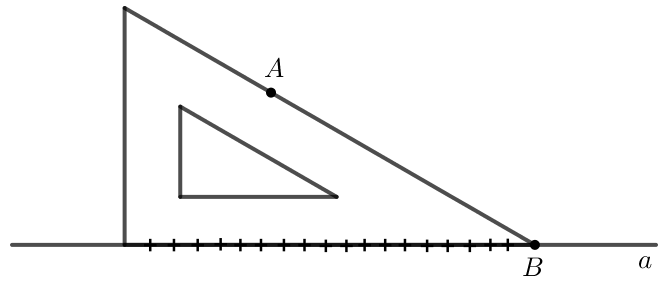
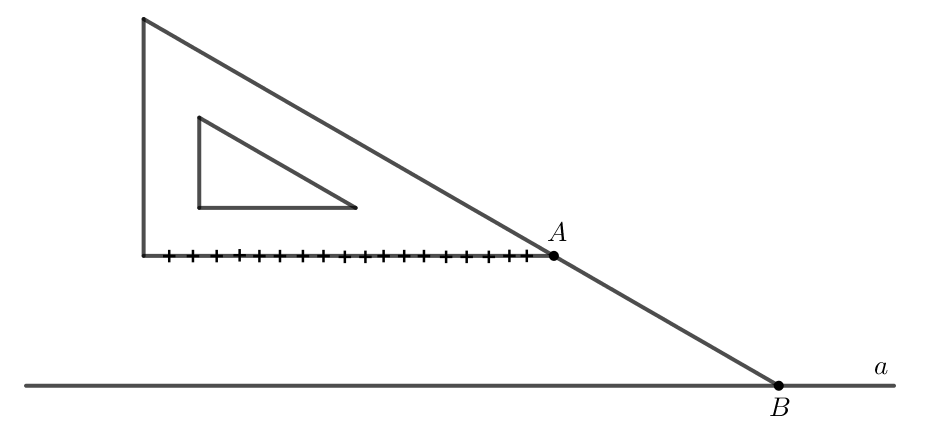
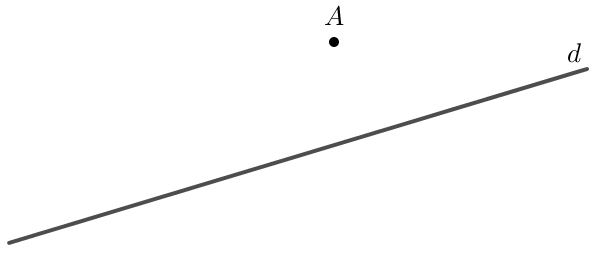
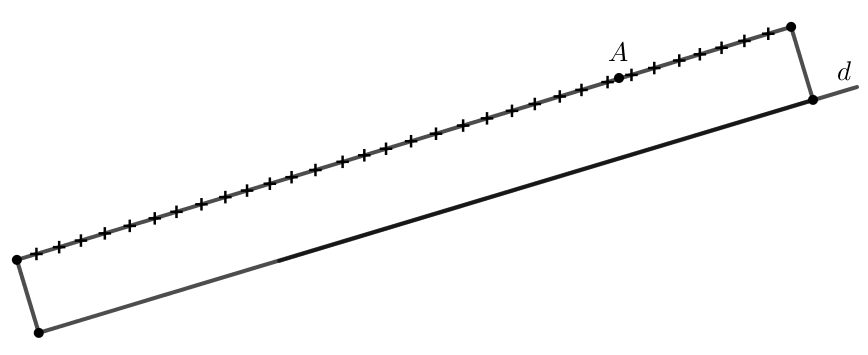
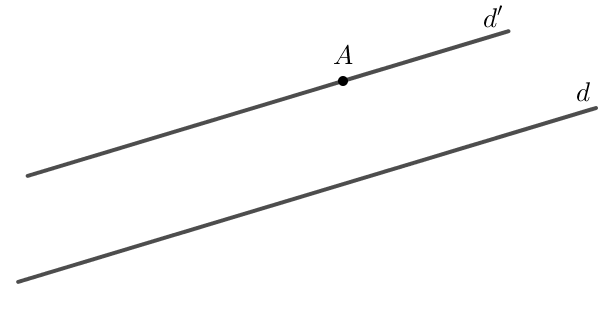
+ Muốn vẽ đường thẳng đi qua một điểm và song song với một đường thẳng cho trước bằng góc 60° của êke ta làm như sau:
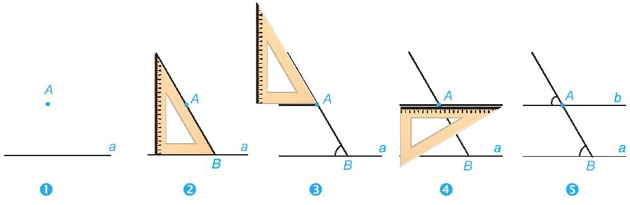
+ Tương tự ta có thể dùng góc vuông hoặc góc 30° của êke (thay cho góc 60°) để vẽ đường thẳng đi qua một điểm và song song với đường thẳng cho trước.
Bài tập Hai đường thẳng song song và dấu hiệu nhận biết
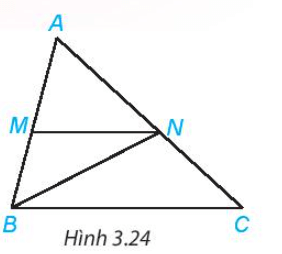
Bài 1. Cho hình vẽ:
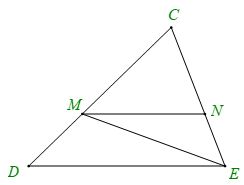
a) Tìm một góc ở vị trí so le trong với góc DEM.
b) Tìm một góc ở vị trí đồng vị với góc CMN.
c) Tìm một góc ở vị trí trong cùng phía với góc MNE.
Hướng dẫn giải
a) Có ME cắt MN và DE nên góc ở vị trí so le trong với góc DEM là góc EMN.
b) Có CD cắt MN và DE nên góc ở vị trí đồng vị với góc CMN là góc CDE (hay MDE).
c) Có CE cắt MN và DE nên góc ở vị trí trong cùng phía với góc MNE là góc NED (hay CED).
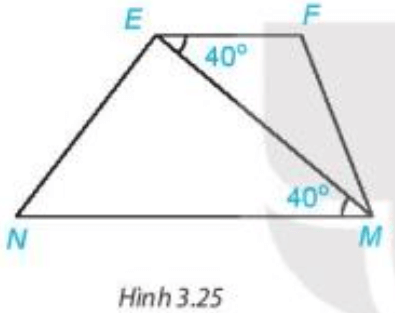
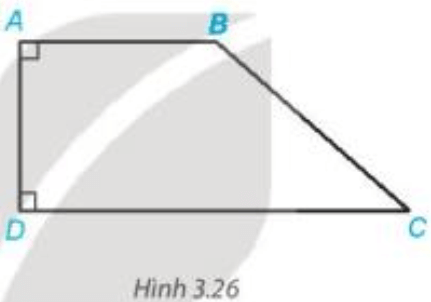
Bài 2. Cho các hình dưới đây, hãy giải thích tại sao .
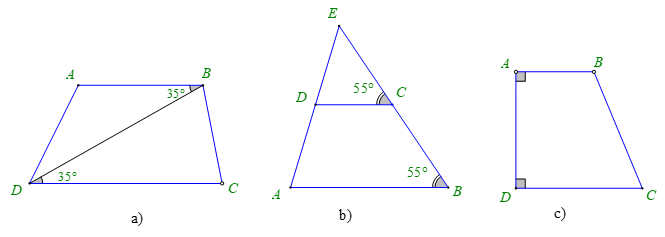
Hướng dẫn giải
a) Ta có:
Mà hai góc ở vị trí so le trong.
Do đó (dấu hiệu nhận biết hai đường thẳng song song).
b) Ta có:
Mà hai góc ở vị trí đồng vị.
Do đó (dấu hiệu nhận biết hai đường thẳng song song).
c) Ta có: và
Do đó: (dấu hiệu nhận biết hai đường thẳng song song).
Bài 3. Hãy vẽ hai đoạn thẳng AB và MN sao cho và .
Hướng dẫn giải
+ Vẽ đoạn thẳng AB với độ dài bất kì.

+ Dùng góc của êke vẽ tiếp theo các bước dưới đây.
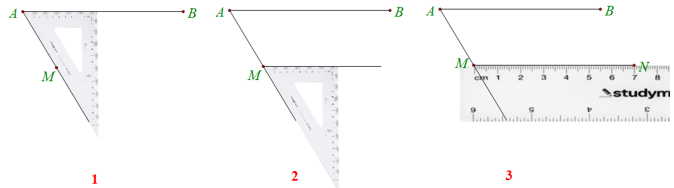
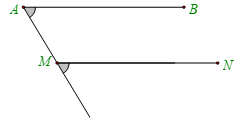
+ Ta được và .
Học tốt Hai đường thẳng song song và dấu hiệu nhận biết
Các bài học để học tốt Hai đường thẳng song song và dấu hiệu nhận biết Toán lớp 7 hay khác: