Toán 9 Cánh diều Bài 2: Một số phép tính về căn bậc hai của số thực
Giải Toán 9 | No tags
Mục lục
- Đang tải mục lục...
Khởi động trang 55 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Khởi động trang 55 Toán 9 Tập 1:
Khi một quả bóng rổ được thả xuống, nó sẽ nảy trở lại, nhưng do tiêu hao năng lượng nên nó không đạt được chiều cao như lúc bắt đầu. Hệ số phục hồi của quả bóng rổ được tính theo công thức , trong đó H là độ cao mà quả bóng được thả rơi và h là độ cao mà quả bóng bật lại.
(Nguồn: Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby, năm 2017)
Một quả bóng rổ rơi từ độ cao 3,24 m và bật lại độ cao 2,25 m. Làm thế nào để viết hệ số phục hồi của quả bóng đó dưới dạng phân số?
Lời giải:
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Thay H = 3,24 m và h = 2,25 m, ta được:
Vậy .
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Hoạt động 1 trang 55 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Hoạt động 1 trang 55 Toán 9 Tập 1: So sánh:
a) và |4|;
b) và |–5|.
Lời giải:
a) Ta có: = = 4 và |4| = 4.
Vậy = |4|.
b) Ta có = 5 và |–5| = 5.
Vậy = |-5|.
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Luyện tập 1 trang 55 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Luyện tập 1 trang 55 Toán 9 Tập 1: Áp dụng quy tắc về căn bậc hai của một bình phương, hãy tính:
a) ;
b) ;
c) .
Lời giải:
a) = |35| = 35
b) = 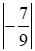
c) = |1-|.
Do 1 < 2 nên < hay 1 < do đó 1 - < 0.
Vì thế, ta có |1-| = - 1.
Vậy = |1-| = - 1.
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Hoạt động 2 trang 56 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Hoạt động 2 trang 56 Toán 9 Tập 1: So sánh: và
Lời giải:
Ta có:
⦁|10| = 10;
⦁ = 2.5 = 10.
Vậy =
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Luyện tập 2 trang 56 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Luyện tập 2 trang 56 Toán 9 Tập 1: Áp dụng quy tắc về căn bậc hai của một tích, hãy tính:
a) ;
b) ;
c) .
Lời giải:
a) = = 5.11 = 55.
b) = 
c) = 52.
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Hoạt động 3 trang 57 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Hoạt động 3 trang 57 Toán 9 Tập 1: So sánh: và
Lời giải:
Ta có: = 
Vậy
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Luyện tập 3 trang 57 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Luyện tập 3 trang 57 Toán 9 Tập 1: Trong tình huống nêu ra ở phần mở đầu, viết hệ số phục hồi của quả bóng rổ dưới dạng phân số.
Lời giải:
Thay H = 3,24 m và h = 2,25 m, ta được:
Vậy
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Hoạt động 4 trang 57 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Hoạt động 4 trang 57 Toán 9 Tập 1: So sánh:
a) và
b) và
Lời giải:
a) Ta có:
Vậy
b) Ta có = |-5|. = 5 và -(-5) = 5.
Vậy
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Luyện tập 4 trang 58 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Luyện tập 4 trang 58 Toán 9 Tập 1: Rút gọn biểu thức:
Lời giải:
Ta có:
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Hoạt động 5 trang 58 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Hoạt động 5 trang 58 Toán 9 Tập 1: So sánh:
a) 3 và
b) -5 và
Lời giải:
Ta có:
a) = 3. Vậy 3 = .
b) = -|-5| = -5. Vậy -5 = .
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Luyện tập 5 trang 59 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Luyện tập 5 trang 59 Toán 9 Tập 1: Rút gọn biểu thức:
a) -7;
b) 6 -
Lời giải:
a) -7 = - = -.
b) 6 - = - = - = - = 0.
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Bài 1 trang 59 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Bài 1 trang 59 Toán 9 Tập 1: Áp dụng quy tắc về căn bậc hai của một bình phương, hãy tính:
a)
b)
c)
Lời giải:
a) = |25| = 25.
b) = |-0,16| = 0,16.
c) = | - 3|.
Vì 7 < 9 nên < hay <3 do đó -3 < 0.
Vì thế, ta có |-3| = 3-.
Vậy = |-3|= 3-.
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Bài 2 trang 59 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Bài 2 trang 59 Toán 9 Tập 1: Áp dụng quy tắc về căn bậc hai của một tích, hãy tính:
a) ;
b) ;
c)
d)
Lời giải:
a) = 6.9 = 54.
b) = 7.11.13 = 1 001.
c)
d)
= 2.
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Bài 3 trang 59 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Bài 3 trang 59 Toán 9 Tập 1: Áp dụng quy tắc về căn bậc hai của một thương, hãy tính:
a) ;
b)
c)
d)
Lời giải:
a)
b)
c)
d)
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Bài 4 trang 59 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Bài 4 trang 59 Toán 9 Tập 1: Áp dụng quy tắc đưa thừa số ra ngoài dấu căn bậc hai, hãy rút gọn biểu thức:
a)
b)
c)
Lời giải:
a)
b)
c)
= 2.0,7 = 1,4.
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Bài 5 trang 59 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Bài 5 trang 59 Toán 9 Tập 1: Áp dụng quy tắc đưa thừa số vào trong dấu căn bậc hai, hãy rút gọn biểu thức:
a) ;
b)
Lời giải:
a)
b)
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Bài 6 trang 60 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Bài 6 trang 60 Toán 9 Tập 1: So sánh:
a) và
b) và 5;
c) 3 và .
Lời giải:
a) Ta có: = .
Vì 21 < 22 nên hay
Vậy
b) Ta có: và 5 =
Vì 26 > 25 nên hay
Vậy
c) Ta có:
Vì 63 < 65 nên hay
Vậy
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Bài 7 trang 60 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Bài 7 trang 60 Toán 9 Tập 1: Cho tam giác đều ABC có độ dài cạnh là a. Tính độ dài đường cao AH của tam giác ABC theo a.
Lời giải:
Xét ∆ABC đều có AH là đường cao nên đồng thời là đường trung tuyến của tam giác, do đó H là trung điểm của BC.
Suy ra HC =
Xét ∆AHC vuông tại H, theo định lí Pythagore, ta có:
AC2 = AH2 + HC2
Suy ra AH2 = AC2 - HC2 = a2 -
Do đó AH = = 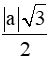
Vậy độ dài đường cao AH của tam giác ABC là .
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Bài 8 trang 60 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Bài 8 trang 60 Toán 9 Tập 1: Trong Vật lí, ta có định luật Joule – Lenz để tính nhiệt lượng toả ra ở dây dẫn khi có dòng điện chạy qua:
Q = I2Rt.
Trong đó: Q là nhiệt lượng toả ra trên dây dẫn tính theo Jun (J);
I là cường độ dòng điện chạy trong dây dẫn tính theo Ampe (A);
R là điện trở dây dẫn tính theo Ohm (Ω);
t là thời gian dòng điện chạy qua dây dẫn tính theo giây.
Áp dụng công thức trên để giải bài toán sau: Một bếp điện khi hoạt động bình thường có điện trở R = 80 Ω. Tính cường độ dòng điện chạy trong dây dẫn, biết nhiệt lượng mà dây dẫn toả ra trong 1 giây là 500 J.
Lời giải:
Theo bài, ta có R = 80 (Ω), t = 1 (s) và Q = 500 (J).
Áp dụng công thức Q = I2RT, ta có: 500 = I2.80.1
Suy ra 80I2 = 500, nên
Do đó I = = 2,5 (A) (do I > 0).
Vậy cường độ dòng điện chạy trong dây dẫn là 2,5 Ampe.
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:
Bài 9 trang 60 Toán 9 Tập 1 Cánh diều
Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều
Bài 9 trang 60 Toán 9 Tập 1: Tốc độ gần đúng của một ô tô ngay trước khi đạp phanh được tính theo công thức v = , trong đó v (m/s) là tốc độ của ô tô, d (m) là chiều dài của vết trượt tính từ thời điểm đạp phanh cho đến khi ô tô dừng lại trên đường, λ là hệ số cản lăn của mặt đường, g = 9,8 m/s2 (Nguồn: Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby, năm 2017). Nếu một chiếc ô tô để lại vết trượt dài khoảng 20 m trên đường nhựa thì tốc độ của ô tô trước khi đạp phanh là khoảng bao nhiêu mét trên giây (làm tròn kết quả đến hàng đơn vị)? Biết rằng hệ số cản lăn của đường nhựa là λ 0,7.
Lời giải:
Theo bài, ta có λ = 0,7; d = 20 (m) ; g = 9,8 m/s2.
Do đó tốc độ của ô tô đó trước khi đạp phanh là:
Vậy tốc độ của ô tô trước khi đạp phanh là khoảng 17 m/s.
Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác:


