Thực hành 12 trang 59 Toán 12 Tập 2 Chân trời sáng tạo

Giải Toán 12 Bài 2: Phương trình đường thẳng trong không gian - Chân trời sáng tạo

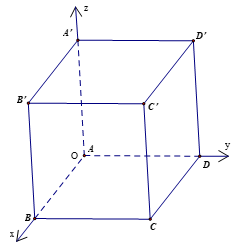
Thực hành 12 trang 59 Toán 12 Tập 2: Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A'B'C'D'. Cho biết A(0; 0; 0), B(1; 0; 0), D(0; 5; 0), A'(0; 0; 3). Tính góc giữa:

a) hai đường thẳng AC và BA';

b) hai mặt phẳng (BB'D'D) và (AA'C'C);

c) đường thẳng AC' và mặt phẳng (A'BD).

Lời giải:

Chọn hệ trục tọa độ như hình vẽ với O trùng với A.

Ta có A'(0; 0; 3), B(1; 0; 0), A(0; 0; 0), C(1; 5; 0), B'(1; 0; 3), D(0; 5; 0), C'(1; 5; 3)

a) Đường thẳng AC nhận $\overrightarrow{AC}=\left(1;5;0\right)$ làm vectơ chỉ phương.

Đường thẳng BA' nhận $\overrightarrow{B{A}^{\text{'}}}=\left(-1;0;3\right)$ làm vectơ chỉ phương.

Khi đó $\cos \left(AC,B{A}^{\text{'}}\right)=\frac{\left|1.\left(-1\right)+5.0+0.3\right|}{\sqrt{1^2+5^2}.\sqrt{{\left(-1\right)}^2+3^2}}=\frac{1}{2\sqrt{65}}$

Suy ra (AC, BA') ≈ 86,44°.

b) Ta có $\overrightarrow{B{B}^{\text{'}}}=\left(0;0;3\right),\overrightarrow{BD}=\left(-1;5;0\right)$, $\overrightarrow{AC}=\left(1;5;0\right)$, $\overrightarrow{A{A}^{\text{'}}}=\left(0;0;3\right)$.

Ta có $\left[\overrightarrow{B{B}^{\text{'}}},\overrightarrow{BD}\right]=\left(-15;-3;0\right)$, $\left[\overrightarrow{AC},\overrightarrow{A{A}^{\text{'}}}\right]=\left(15;-3;0\right)$.

Mặt phẳng (BB'D'D) nhận $\overrightarrow{n}=-\frac{1}{3}\left[\overrightarrow{B{B}^{\text{'}}},\overrightarrow{BD}\right]=\left(5;1;0\right)$ làm vectơ pháp tuyến.

Mặt phẳng (AA'C'C) nhận $\overrightarrow{n^{\text{'}}}=\frac{1}{3}\left[\overrightarrow{AC},\overrightarrow{A{A}^{\text{'}}}\right]=\left(5;-1;0\right)$ làm vectơ pháp tuyến.

Khi đó $\cos \left(\left(B{B}^{\text{'}}{D}^{\text{'}}D\right),\left(A{A}^{\text{'}}{C}^{\text{'}}C\right)\right)=\frac{\left|5.5+1.\left(-1\right)+0.0\right|}{\sqrt{5^2+1}.\sqrt{5^2+1}}=\frac{24}{26}=\frac{12}{13}$.

Suy ra ((BB'D'D), (AA'C'C)) ≈ 22,62°.

c) Ta có $\overrightarrow{A{C}^{\text{'}}}=\left(1;5;3\right)$, $\overrightarrow{A^{\text{'}}B}=\left(1;0;-3\right),\overrightarrow{A^{\text{'}}D}=\left(0;5;-3\right)$, $\left[\overrightarrow{A^{\text{'}}B},\overrightarrow{A^{\text{'}}D}\right]=\left(15;3;5\right)$.

Đường thẳng AC' nhận $\overrightarrow{A{C}^{\text{'}}}=\left(1;5;3\right)$ làm vectơ chỉ phương.

Mặt phẳng (A'BD) nhận $\overrightarrow{n}=\left[\overrightarrow{A^{\text{'}}B},\overrightarrow{A^{\text{'}}D}\right]=\left(15;3;5\right)$ làm vectơ pháp tuyến.

Ta có $\sin \left(A{C}^{\text{'}},\left(A^{\text{'}}BD\right)\right)=\frac{\left|1.15+5.3+3.5\right|}{\sqrt{1^2+5^2+3^2}.\sqrt{{15}^2+3^2+5^2}}=\frac{45}{7\sqrt{185}}$.

Suy ra (AC', (A'BD)) ≈ 28,21°.

Lời giải bài tập Toán 12 Bài 2: Phương trình đường thẳng trong không gian hay, chi tiết khác: