Bài 2.6 trang 58 Toán 12 Kết nối tri thức Tập 1

Giải Toán 12 Bài 6: Vectơ trong không gian - Kết nối tri thức

Bài 2.6 trang 58 Toán 12 Tập 1: Cho hình chóp tứ giác S.ABCD. Chứng minh rằng tứ giác ABCD là hình bình hành nếu và chỉ nếu $\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}$.

Lời giải:

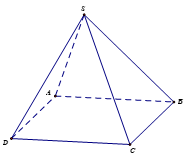
Chứng minh: Nếu ABCD là hình bình hành thì $\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}$ .

Vì ABCD là hình bình hành nên

  $\overrightarrow{AD}=\overrightarrow{BC}$ $\iff \overrightarrow{SD}-\overrightarrow{SA}=\overrightarrow{SC}-\overrightarrow{SB}$$\iff \overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}$.

Chứng minh: Nếu $\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}$  thì ABCD là hình bình hành.

Có $\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}$ $\iff \overrightarrow{SA}-\overrightarrow{SD}=\overrightarrow{SB}-\overrightarrow{SC}$$\iff \overrightarrow{DA}=\overrightarrow{CB}$ .

Suy ra ABCD là hình bình hành.

Lời giải bài tập Toán 12 Bài 6: Vectơ trong không gian hay, chi tiết khác: