HĐ6 trang 46 Toán 12 Tập 2 - Kết nối tri thức

Giải Toán 12 Bài 15: Phương trình đường thẳng trong không gian - Kết nối tri thức

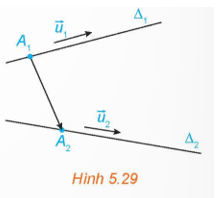
HĐ6 trang 46 Toán 12 Tập 2: Trong không gian Oxyz, cho hai đường thẳng ∆₁; ∆₂ lần lượt đi qua các điểm A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂) và tương ứng có vectơ chỉ phương $\overrightarrow{u_1}=\left(a_1;b_1;c_1\right),\overrightarrow{u_2}=\left(a_2;b_2;c_2\right)$ (H.5.29).

a) Tìm điều kiện đối với $\overrightarrow{u_1}$ và $\overrightarrow{u_2}$ để ∆₁ và ∆₂ song song hoặc trùng nhau.

b) Giả sử $\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]\ne \overrightarrow{0}$ và $\overrightarrow{A_1{A}_2}.\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]=0$ thì ∆₁ và ∆₂ có cắt nhau hay không?

c) Giả sử $\overrightarrow{A_1{A}_2}.\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]\ne 0$ thì ∆₁ và ∆₂ có chéo nhau hay không?

Lời giải:

a) ∆₁ // ∆₂$\iff \left\{\begin{array}{l}\overrightarrow{u_1}=k\overrightarrow{u_2}\\ A_1\notin {\Delta }_2\end{array}\right.$ .

_∆1 ≡ ∆₂$\iff \left\{\begin{array}{l}\overrightarrow{u_1}=k\overrightarrow{u_2}\\ A_1\in {\Delta }_2\end{array}\right.$ .

b) ∆₁ và ∆₂ cắt nhau khi và chỉ khi $\overrightarrow{u_1}$ và $\overrightarrow{u_2}$ không cùng phương và $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ và $\overrightarrow{A_1{A}_2}$ đồng phẳng. Tức là $\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]\ne \overrightarrow{0}$ và $\overrightarrow{A_1{A}_2}.\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]=0$.

c) ∆₁ và ∆₂ chéo nhau khi và chỉ khi $\overrightarrow{u_1}$, $\overrightarrow{u_2}$ và $\overrightarrow{A_1{A}_2}$  không đồng phẳng. Tức là: $\overrightarrow{A_1{A}_2}.\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]\ne 0$

Lời giải bài tập Toán 12 Bài 15: Phương trình đường thẳng trong không gian hay, chi tiết khác: