Vận dụng 6 trang 42 Toán 12 Tập 2 Chân trời sáng tạo

Giải Toán 12 Bài 1: Phương trình mặt phẳng - Chân trời sáng tạo

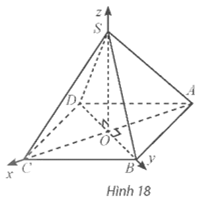
Vận dụng 6 trang 42 Toán 12 Tập 2: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng $a\sqrt{2}$, chiều cao bằng 2a và O là tâm của đáy. Bằng cách thiết lập hệ trục tọa độ Oxyz như Hình 18, tính khoảng cách từ điểm C đến mặt phẳng (SAB).

Lời giải:

Vì ABCD là hình vuông cạnh $a\sqrt{2}$ và O là tâm của hình vuông nên ta có:

OA=OB=OC=OD=a.

Khi đó ta có O(0; 0; 0), A(−a; 0; 0), B(0; a; 0), S(0; 0; 2a), C(a; 0; 0).

Mặt phẳng (SAB) đi qua A(−a; 0; 0), B(0; a; 0), S(0; 0; 2a) có phương trình theo đoạn chắn là:

$\frac{x}{-a}+\frac{y}{a}+\frac{z}{2a}=1$ hay −2x + 2y + z = 2a hay −2x + 2y + z – 2a = 0.

Ta có $d\left(C,\left(SAB\right)\right)=\frac{\left|-2a-2a\right|}{\sqrt{{\left(-2\right)}^2+2^2+1^2}}=\frac{4a}{3}$.

Vậy $d\left(C,\left(SAB\right)\right)=\frac{4}{3}a$

Lời giải bài tập Toán 12 Bài 1: Phương trình mặt phẳng hay, chi tiết khác: